Интерференция света. 2.1 Скорость света в среде:

2.1 Скорость света в среде:

,

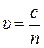где c – скорость света в вакууме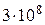, с = м/с; 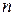– абсолютный показатель преломления среды.

2.2 Оптическая длина пути световой волны:

,

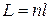где 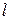− геометрическая длина пути световой волны в среде с показателем преломления n.

2.3 Оптическая разность хода двух световых волн:

.

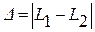2.4 При отражении света от оптически более плотной среды фаза колебаний светового вектора (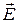) испытывает скачок фазы на 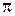. Изменение фазы колебаний на 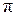приводит к изменению оптического пути световой волны на 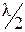. ( 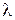- длина волны в вакууме).

2.5 Оптическая разность хода световых волн, отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пластинки или пленки, находящейся в воздухе, рис. 4:

,

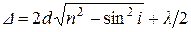где d – толщина пластинки (пленки); i − угол падения луча на пластинку; 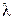− длина световой волны в вакууме.

Слагаемое 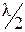учитывает изменение оптической длины пути световой волны при отражении ее от среды, оптически более плотной (в точке А).

2.6 Условие максимумов интенсивности света при интерференции:

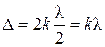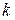( = 0, 1, 2, 3,…).

2.7 Условие минимумов интенсивности света при интерференции:

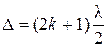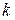( = 0, 1, 2, 3,…).

2.8 Кольца Ньютона. При отражении света от поверхностей воздушной прослойки, образованной между стеклянной пластинкой и соприкасающейся к ней выпуклой поверхностью линзы с радиусом кривизны 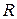, рис. 5, возникающая интерференционная картина носит название колец Ньютона.

· В отраженном свете оптическая разность хода лучей при отражении от поверхностей воздушной прослойки:

.

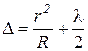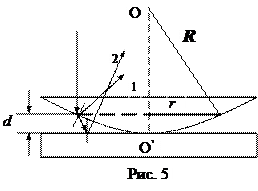· Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем):

,

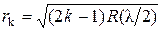где k – номер кольца (k = 1, 2, 3,…);

R – радиус кривизны поверхности линзы.

· Радиусы темных колец в отраженном свете (или светлых в проходящем):

.

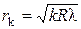Пример 4. Поверхности стеклянного клина (n = 1,5) образуют между собой угол 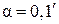. На клин падает нормально к его поверхности пучок монохроматических лучей длинной волны 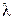= 0,5 мкм (рис. 6). Найти расстояние между полосами.

Дано: n = 1,5; 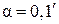; 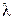= 0,5 мкм = 0,5 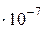м.

Найти: .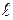

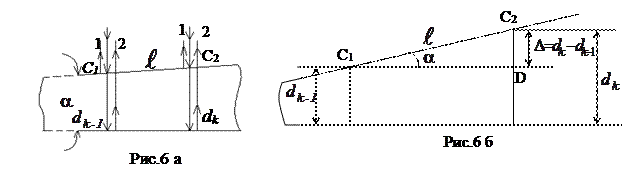Решение. Клин представляет собой частный случай тонкой пленки, имеющей переменную толщину d. Когерентные волны образуются при отражении света от верхней и нижней граней клина. При малых углах
клина 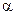когерентные лучи 1 и 2 идут практически параллельно и
интерферируют (рис. 6а). Оптическую разность хода этих лучей находим по формуле

.

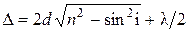В данной задаче угол падения лучей на клин i = 0 и разность хода 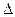приблизительно равна

.

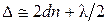Пусть точкам С₁ и С₂ на рис. 6 б соответствуют две соседние светлые интерференционные полосы, тогда для разностей хода 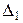и 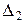в этих точках имеем:

,

,

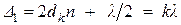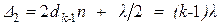где d _k, d _k-1 – толщины клина в тех местах, где наблюдаются светлые полосы; k, (k -1) – номера полос (номера интерференционных максимумов).

Вычитая почленно эти два равенства друг из друга, получим:

,

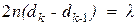откуда

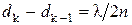. (1)

Искомое расстояние между соседними полосами 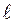можно легко выразить из :

,

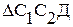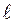
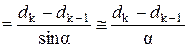sin 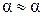, так как по условию задачи угол 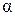очень мал.

Подставляя в последнюю формулу вместо разности 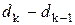ее значение из формулы (1), получим:

.

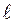
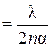Найдем численное значение 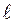( 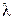=0,5 мкм=0,5 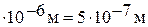, n = 1,5).

Переведем 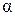в радианы ( 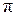= 3,14):

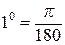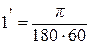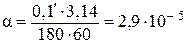рад; рад;

рад.

Тогда получим:

.

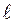
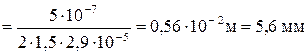Ответ: 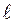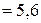мм.

Эта задача может быть решена и в обратном порядке, то есть по расстоянию между интерференционными полосами 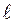можно найти угол клина .

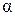Дата добавления: 2015-06-04