Вопрос. Экономическая динамика – процесс последовательного, упорядоченного перехода от одних состояний к другим

Вопрос

Вопрос.

Экономическая динамика – процесс последовательного, упорядоченного перехода от одних состояний к другим.

Траектория – это отображения процесса развития при котором каждому значению переменной времени ставят в соответствие с состоянием экономики в данный момент времени.

Траектория описывает процесс развития как функцию от времени т.е y=f(t)/

Составными элементами ряда динамики являются цифровые значения показателей называемые уровнями.

В качестве начальной границы времени обычно принимают ноль (0), состояние экономики в этот момент называется начальным и как правило задают.

Правая граница временного интервала модели называется её горизонтом.

Длина временного ряда – это время прошедшее от начального момента наблюдения до конечного. Она = числу уровней входящих во временной ряд.

Классификация временных рядов в зависимости от способа учета и факторов времени и отражения во временном показателе.

В зависимости от способа учета показателей времени ряды динамики деляться на следующие виды:

1) Непрерывные (с непрерывным меняющимся временем) когда для переменной времени допускаются все значения множество вещественных чисел.

2) Дискретные (динамические) в которых переменные времени принимают значение только целого числа.

По способу выражения уровней ряды динамики бывают:

1) Рядами динамики абсолютных величин

2) Рядами динамики относительных величин

3) Рядами динамики средних величин.

Важной задачей при анализе временных рядов является определение основной тенденции развития, которую называют трендом.

Экономико-математическая модель в которой развитие моделируемой экономической системы выражено через тренд е основных показателей называется трендовой моделью.

Для характеристики интенсивности изменения уровней динамики во времени используется следующая система показателей:

1) Абсолютный прирост (цепной, базисный, средний)

2) Темпы роста (цепной, базисный, средний)

3) Абсолютные значения 1% прироста (цепное и среднее)

При анализе временных рядов уровни должны быть сопоставимы.

Условия сопостовимости:

1) по территории

2) по кругу охватываемых объектов

3) по временным периодам

4) по масштабу измерения

5) по масштабу цен

6) по структуре совокупности, для которой они вычисляются.

При изучении развития явления во времени часто возникает необходимость оценить степень зависимости изучаемых показателей от их значений в предыдущие периоды.
Эта задача решается методом кореллирования (временная зависимость).
Автокорелляция во временном ряду - это зависимость значений уровней временного ряда от предыдущих (сдвиг на 1), предпредыдущих (сдвиг на 2) и так далее уровней того же временного ряда.
График автокорреляционной функци называется корреллограммой.

Во временных рядах экономических процессов могут иметь место достаточно регулярные колебания. Если они имеют периодический или близкий к нему характер и заканчиваются в течение одного года, то их называют сезонными колебаниями.
В тех случаях, когда периоды колебания составляют несколько лет, то говорят, что во временном ряду присутствует циклическая компонента.
Тренд, сезонные и циклические компоненты называются регулярными или систематическими колебаниями временного ряда.
Часть временного ряда, остающаяся после выделения из него регулярных компонент, представляет собой случайную нерегулярную компоненту.
Таким образом, в составе динамического ряда выделяются 4 компоненты:

1) главная или вековая тенденция (тренд);

2) регулярные колебания относительно тренда;

3) сезонные колебания;

4) остаток (случайная компонента), отражающая действия факторов стахостического характера.

Наличие данных компонент зависит от сущности процесса выраженного динамическим рядом. Например: Для рядов, характеризующих макроэкономические процессы в экономике, типично присутствие по крайней мере главной и случайной компоненты.
За основу типизации экономических явлений обычно принимают динамику абсолютных приростов. В данном случае можно выделить как минимум 4 типа экономического развития:

1. Постоянный рост, характеризующийся постоянным или близким к нему абсолютным приростом. (А_цеп=const)
Данный типа развития описывается прямолинейной функцией

y =a₀+a₁t,где a₀ – теоретиеский уровень базисного уровня; a₁ – постоянный ежегодный абсолютный прирост

2. Увеличивающийся рост, в рамках которого выделяют 2 типа роста:
1) развитие с увеличивавшимся абсолютным приростом, который описывается показательной или экспоненциальной функцией

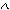y =a₀(1+a₁)^t – показательная.

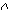y =a₀е^a1t - экспоненциальная функция.

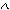2) рост с постоянным абсолютным ускорением, описывается пораболой 2-ого порядка.

y =a₀+a₁t+a₂t²

Данная функция хорошо отражает тенденции развития многих экономических процессов, когда абсолютнsе приростs продолжают увеличиваться, а темпы прироста уменьшаются.

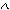
3. Уменьшающийся рост, представляющийся в виде:
1) уменьшающийся рост, не имеющий предела, моделями тренда в данном случае могут служить функции с положительными параметрами линейно-логарифмическая y =a₀+a₁lnt и степенная y =a₀a₁^t.

2) уменьшающийся рост имеющий предел (насыщение). Функция данного типа имеет предел. Например гипербола 1-ого порядка y =a₀+ a₁/t, при а₀, а₁ >0.

4. Рост с качественным изменением характеристик на протяжении рассматриваемого периода. Характерным свойством данных терндовых моделей является наличие точки перегиба, в которой с точки зрения математики абсолютное ускорение равно 0 и меняет свой знак.

Более сложные задачи анализа динамики с меняющимися тенденциями развития решаются с помощью квазиполиномов и сплайн-функции.
Они могут содержать как куски одинаковых функций, различающиеся только значениями параметров, так и разные виды функции.
При выборе функций важно учитывать цель анализа.

Для ретроспективного анализа необходимо, что бы функция хорошо сглаживала весь исходный динамический ряд. Если трендовая модель используется для прогнозирования, то предпочтение отдается функции, имеющей лучшие характеристики апраксимации для последней части динамического ряда. Это объясняется тем, что тенденция развития, складывающаяся в конце ретроспективного периода оказывает как правило наибольшее воздействие на будущее развитие.

Дата добавления: 2015-06-04