
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обработка результатов нескольких серий измерений одной и той же величины
|
|
|
|
Задание 2. При многократных измерениях одной и той же величины получены две серии по 12 результатов измерений в каждой. Эти результаты после внесения поправок представлены в таблице 5. Исключить ошибки из результатов измерений.
Исходные данные (табл. 4).
Таблица 4
| Серия 1 | Серия 2 | ||||||
| № измер-ния | Результат измерения | № измерения | Результат измерения | № измерения | Резуль-тат измерения | № измерения | Результат измерения |
Решение. 1. Обрабатываем экспериментальные данные по алгоритму, изложенному в п.п. 1, 2 задания 1, при этом:
– определяем оценки результата измерения 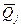 и среднеквадратического отклонения
и среднеквадратического отклонения 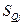 , j = 1,2, используя таблицу 5 и этапы a-c:
, j = 1,2, используя таблицу 5 и этапы a-c:
Таблица 5
| Серия 1 | Серия 2 | ||||||
| № измерения | Q1i | 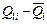
| 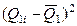
| № измерения | Q2i | 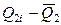
| 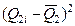
|
| -2,1667 | 4,6944 | -0,7500 | 0,5625 | ||||
| 0,8333 | 0,6944 | -0,7500 | 0,5625 | ||||
| 1,8333 | 3,3611 | -0,7500 | 0,5625 | ||||
| 1,8333 | 3,3611 | -0,7500 | 0,5625 |
Продолжение табл. 5
| № измерения | Q1i | 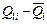
| 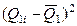
| № измерения | Q2i | 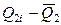
| 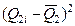
|
| -1,1667 | 1,3611 | 0,2500 | 0,0625 | ||||
| -1,1667 | 1,3611 | 0,2500 | 0,0625 | ||||
| -1,1667 | 1,3611 | -0,7500 | 0,5625 | ||||
| -1,1667 | 1,3611 | -1,7500 | 3,0625 | ||||
| -3,1667 | 10,0278 | -2,7500 | 7,5625 | ||||
| -4,1667 | 17,3611 | -2,7500 | 7,5625 | ||||
| 7,8333 | 61,3611 | -0,7500 | 0,5625 | ||||
| 1,8333 | 3,3611 | 11,2500 | 126,5625 | ||||
| Σ | 109,6667 | Σ | 148,2500 |
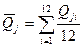
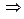
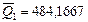 ,
, 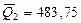 ;
;
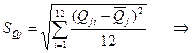
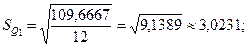
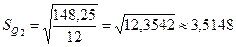 ;
;
– обнаруживаем и исключаем ошибки:
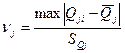
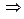
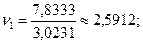
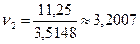 ;
;
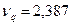 при n = 12;
при n = 12;
– сравниваем 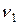 и
и 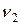 с
с 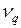 :
: 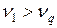 и
и 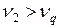 . Результаты измерения Q1,11 и Q2,12 являются ошибочными, они должны быть отброшены.
. Результаты измерения Q1,11 и Q2,12 являются ошибочными, они должны быть отброшены.
Повторяем вычисления, при этом отбрасываем измерения 11 из серии №1 и 12 из серии №2 и используем таблицу 6:
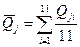
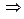
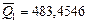 ,
, 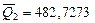 ;
;
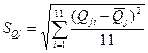
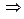
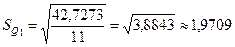 ;
; 
Таблица 6
| Серия 1 | Серия 2 | ||||||
| № измерения | Q1i | 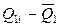
|
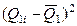
| № измерения | Q2i | 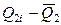
|
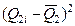
|
| -1,4545 | 2,1157 | 0,2727 | 0,0744 | ||||
| 1,5455 | 2,3884 | 0,2727 | 0,0744 | ||||
| 2,5455 | 6,4793 | 0,2727 | 0,0744 | ||||
| 2,5455 | 6,4793 | 0,2727 | 0,0744 | ||||
| -0,4545 | 0,2066 | 1,2727 | 1,6198 |
Продолжение табл. 6
| Серия 1 | Серия 2 | ||||||
| № измерения | Q1i | 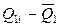
|
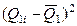
| № измерения | Q2i | 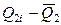
|
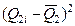
|
| -0,4545 | 0,2066 | 1,2727 | 1,6198 | ||||
| -0,4545 | 0,2066 | 0,2727 | 0,0744 | ||||
| -0,4545 | 0,2066 | -0,7273 | 0,5289 | ||||
| -2,4545 | 6,0248 | -1,7273 | 2,9835 | ||||
| -3,4545 | 11,9339 | -1,7273 | 2,9835 | ||||
| 2,5455 | 6,4793 | 0,2727 | 0,0744 | ||||
| Σ | 42,7273 | Σ | 10,1818 |
 ;
; 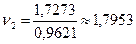 ;
;
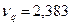 при n = 11.
при n = 11.
Сравниваем 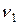 и
и 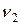 с
с 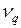 :
: 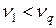 и
и 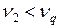 . Результаты измерений 10 из серии №1 и 9 из серии №2 не являются ошибочными и окончательно остается 11 измерений для обеих серий, т.е. n = 11.
. Результаты измерений 10 из серии №1 и 9 из серии №2 не являются ошибочными и окончательно остается 11 измерений для обеих серий, т.е. n = 11.
2. Считая результаты измерений распределенными нормально с вероятностью  , проверим значимость различия средних арифметических серий. Для этого:
, проверим значимость различия средних арифметических серий. Для этого:
– вычисляем моменты закона распределения разности:
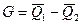
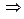
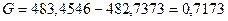 , n 1 = n 2 = n;
, n 1 = n 2 = n;
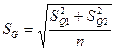
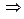
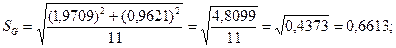
– задавшись доверительной вероятностью P = 0,95, определяем из Приложения, таблица 3 интегральной функции нормированного нормального распределения Ф(t) значение t:
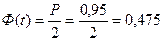
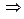 t = 1,96;
t = 1,96;
и сравниваем 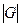 с
с 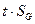 , при
, при 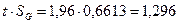 :
: 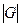 <
< 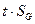 . Различия между средними арифметическими в сериях с доверительной вероятностью P можно признать незначимыми.
. Различия между средними арифметическими в сериях с доверительной вероятностью P можно признать незначимыми.
3. Обрабатываем совместно результаты измерения обеих серий с учетом весовых коэффициентов:
- определяем оценки результата измерения 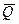 и среднеквадратического отклонения S:
и среднеквадратического отклонения S:
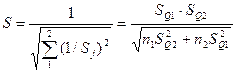 ;
;
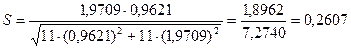 ;
;
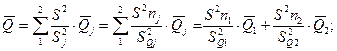
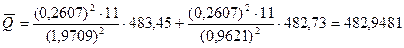 .
.
- задавшись доверительной вероятностью P = 0,95, определяем по таблице t = 1,96 и доверительный интервал:
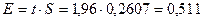 ;
;
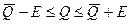 ;
;
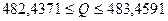 .
.
Лабораторная работа №2
Вычисление структурных средних величин (СВ)
Задание. Создайте лист Microsoft Excel. Заполните ранжированный ряд из следующих чисел: 20, 22, 90, 20, 26. По этому ряду необходимо найти медиану, моду, среднее арифметическое значение.
1. Медиана – середина ранжированного ряда, т.е. это значение признака х, которое делит ранжированный ряд пополам.
Выберите из списка функций Статистические – МЕДИАНА, нажмите ОК. В поле Число 1, выберите интервал вашего ряда, нажмите Enter, а затем ОК. Полученное значение медианы должно быть равным 22.
2. Мода – наиболее часто встречающееся значение х в ряду.
Выберите из списка функций Статистические – МОДА, нажмите ОК. В поле Число 1, выберите интервал вашего ряда, нажмите Enter, а затем ОК. Полученное значение моды должно быть равным 20.
3. Среднее арифметическое значение: выбираем из списка функций Статистические – СРЗНАЧ, нажмите ОК. В поле Число 1 выберите интервал вашего ряда, нажмите Enter, а затем ОК. Полученное значение среднего арифметического должно быть равным 35,6.
Упражнение. Дан ранжированный ряд 20, 20, 22, 26, 90, 80. Найти медиану, моду, среднее арифметическое.
Ответы: Медиана = 24, Мода = 20, Среднее арифметическое
значение = 43.
Выполните задание по ранжированному ряду: 20+ к, 22+ к, 90+ к, 20+ к, 26+ к, к – номер фамилии студента в списке группы.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 660; Нарушение авторских прав?; Мы поможем в написании вашей работы!