Лабораторная работа №4. Проверка адекватности модели парной регрессии

Проверка адекватности модели парной регрессии

Задание

1. Вычислить коэффициент детерминации для полученной модели, используя различные формы представления коэффициента.

2. Проверить значимость коэффициента детерминации на основании
F- теста.

Основная формула:

Σ (y_t - 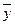)² = Σ (y_эмп - 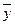)² + Σ (y_t - y_эмп)²,

или

TSS = ESS + RSS,

где TSS – полная сумма квадратов;

ESS - сумма квадратов, объясненная моделью;

RSS – остаточная сумма квадратов.

Ход работы

1. Находим эмпирическое значение y_эмп величины y: выделяем ячейку, в выделенной ячейке ставим знак «=», щелкаем мышью по ячейке, содержащей значение а, ставим в строке формул знак «$» перед буквой и цифрой, чтобы зафиксировать значение, ставим знак «+», щелкаем мышью по ячейке, содержащей значение b, снова ставим в верхней строке формулы знак «$» перед буквой и перед цифрой, чтобы зафиксировать значение, нажимаем знак «*», щелкаем мышью по ячейке, содержащей значение x, нажимаем Enter. Удерживая левую кнопку мыши, протягиваем вниз, чтобы получилось 15 ячеек. Нашли 15 значений y_эмп, соответствующие значениям х.

2. Находим ESS: выделяем одну ячейку, в выделенной ячейке ставим знак «=», открываем скобку, щелкаем мышью по ячейке, содержащей первое значение y_эмп, ставим знак «-», далее щелкаем мышью по ячейке, содержащей среднее значение , фиксируем его в строке формул знаком «$» перед буквой и перед цифрой, закрываем скобку и умножаем на аналогичную скобку, так как нам нужен её квадрат, нажимаем Enter. Удерживая левую кнопку мыши, протягиваем вниз еще на 14 ячеек. Затем находим сумму получившихся значений: щелкаем по ячейке, находящейся ниже этих значений, ставим знак «=», выбираем значок ∑ (автосумма) на панели инструментов и выделяем с помощью мыши все получившиеся значения произведений, нажимаем Enter.

3. Находим TSS: делаем все то же самое, что и в пункте 2, только вычитаем среднее значение не от y_эмп, а от y.

4. Находим RSS: выделяем 1 ячейку, в выделенной ячейке ставим знак «=», открываем скобку, щелкаем мышью по ячейке, содержащей первое значение y, ставим знак «-», далее щелкаем мышью по ячейке, содержащей значение y_эмп, закрываем скобку и умножаем на аналогичную скобку, нажимаем Enter. Удерживая левую кнопку мыши, протягиваем вниз еще на 14 ячеек. Находим сумму получившихся значений: щелкаем по ячейке, находящейся ниже этих значений, ставим знак «=», выбираем значок ∑ (автосумма) на панели инструментов и выделяем с помощью мыши все получившиеся значения произведений, нажимаем Enter.

5. Находим коэффициент детерминации по первой формуле:

R² = ESS/TSS.

Выделяем ячейку, ставим знак «=», щелкаем мышью по ячейке, содержащей значение суммы ESS, ставим знак «/», щелкаем мышью по ячейке, содержащей значение суммы TSS, нажимаем Enter.

6. Находим коэффициент детерминации по второй формуле:

R² = 1- (RSS/TSS).

Выделяем ячейку, ставим знак «=», нажимаем 1, ставим знак «-», затем открываем скобку, щелкаем мышью по ячейке, содержащей значение суммы RSS, ставим знак «/», щелкаем мышью по ячейке, содержащей значение суммы TSS, закрываем скобку, нажимаем Enter.

7. Находим коэффициент детерминации по третьей формуле:

R² = r(y, y_эмп )²,

где

r(y, y_эмп )² =cov(y, y_эмп) / (var(y)*var(y_эмп)),

cov(y, y_эмп)= 1/(t-1)* Σ (y- 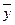)* (y_эмп- ).

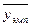Для этого выполняем промежуточные действия:

а) находим 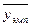аналогично 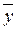из первого задания;

b) находим сумму из формулы ковариации: выделяем ячейку, в выделенной ячейке ставим знак «=», открываем скобку, щелкаем мышью по ячейке, содержащей первое значение y, ставим знак «-», далее щелкаем мышью по ячейке, содержащей значение 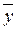, фиксируем его в верхней строке формулы знаком «$» перед буквой и перед цифрой, закрываем скобку, ставим знак «*», открываем скобку, щелкаем мышью по ячейке, содержащей первое значение y_эмп, ставим знак «-», далее щелкаем мышью по ячейке, содержащей значение y_эмп и фиксируем его в верхней строке формулы знаком «$» перед буквой и перед цифрой, закрываем скобку, нажимаем Enter. Удерживая левую кнопку мыши, протягиваем вниз еще на 14 ячеек. Находим сумму получившихся значений: щелкаем по ячейке, находящейся ниже этих значений, ставим знак «=», выбираем значок ∑ (автосумма) на панели инструментов и выделяем с помощью мыши все получившиеся значения произведений, нажимаем Enter;

с) находим ковариацию. Выделяем ячейку, ставим знак «=», нажимаем 1, ставим знак «/» на клавиатуре набираем 14 (так как t =15, в формуле t -1), щелкаем мышью по ячейке, содержащей значение суммы из пункта b, нажимаем Enter;

d) находим var -дисперсию y и y_эмп. Выделяем ячейку, ставим знак «=», выбираем значок f_x на панели инструментов, затем находим ДИСП в окне меню, нажимаем OK, выделяем область по y, которая заносится в поле Число 1. Нажимаем OK. Аналогично находим дисперсию для величины y_эмп;

e) находим произведение дисперсий. Выделяем ячейку, ставим знак «=», щелкаем мышью по ячейке, содержащей значение дисперсии y, ставим знак «*», далее щелкаем мышью по ячейке, содержащей значение дисперсии y_эмп, нажимаем Enter;

f) извлекаем корень из произведения дисперсий. Выделяем ячейку, ставим знак «=», выбираем значок f_x на панели инструментов, затем находим КОРЕНЬ в окне меню, нажимаем OK, выделяем ячейку со значением из пункта e, которая заносится в поле. Нажимаем OK;

g) находим коэффициент корреляции r. Выделяем ячейку, ставим знак «=», щелкаем мышью по ячейке, содержащей значение ковариации из пункта с, ставим знак «/», далее щелкаем мышью по ячейке, содержащей значение корня из пункта f, нажимаем Enter;

h) находим коэффициент детерминации по третьей формуле. Выделяем ячейку, ставим знак «=», щелкаем мышью по ячейке, содержащей значение коэффициента корреляции r из пункта g, ставим знак «*» и щелкаем по той же ячейке, нажимаем Enter.

8. Проверяем адекватность модели с помощью F -теста. Вычисляем значение F -критерия на основе формулы:

F = R²/((1- R²)/(t-2)),

где t =15 - число наблюдений.

Выделяем ячейку, ставим знак «=», щелкаем мышью по ячейке, содержащей значение коэффициента детерминации R² из пункта 6, ставим знак «/», ставим скобки ((, затем 1, ставим знак «-», и щелкаем по той же ячейке R², первую скобку закрываем, ставим знак «/», число 13, вторую скобку закрываем, нажимаем Enter.

9. Находим F табличное для уровней значимости 0,05 и 0,01.

Если F, полученное в пункте 8, больше F табличного для данного уровня значимости, то нулевая гипотеза H₀ отклоняется на этом уровне значимости.

Варианты для парной регрессионной модели

Вариант № 1

Вариант № 2

Вариант № 3

Вариант № 4

Вариант № 5

Вариант № 6

Вариант № 7

Вариант № 8

Вариант № 9

Вариант № 10

Вариант № 11

Вариант № 12

Вариант № 13

Вариант № 14

Вариант № 15

Вариант № 16

Вариант № 17

Вариант № 18

Вариант № 19

Вариант № 20

Вариант № 21

Вариант № 22

Вариант № 23

Вариант № 24

Вариант № 25

Вариант № 26

Вариант № 27

Вариант № 28

Вариант № 29

Вариант № 30

Лабораторная работа №5

Множественная регрессионная модель.

Классическая линейная модель

Классическая (нормальная) модель линейной множественной регрессии (КЛММР) имеет вид:

(1)

где - значение результирующей переменной; 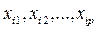- значение 1-го, 2-го,…, р -го регрессора в i- ом наблюдении (i = 1,2,…, n); β_0, β_1, β_p - числовые коэффициенты; ε_i - случайные (стохастические) составляющие или ошибки (возмущения).

Переписывая выражение (1) в виде системы уравнений для различных значений (i = 1,2,…, n), их можно представить в матричном виде:

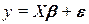, (2)

где - вектор объясняемых переменных;

ε= 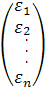- вектор значений ошибки; 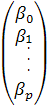- вектор коэффициентов;

X= - матрица объясняющих переменных размером n × (p+1), в которой первый столбец с единичными элементами соответствует в выражении (1) умножению 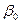на единицу.

Основные предпосылки (гипотезы) КЛММР:

1. Х – детерминированная матрица.

2. Математическое ожидание возмущения ε₀ равно нулю:

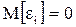(i = 1,2,…, n),

где М[·] знак математического ожидания.

3. Дисперсия возмущения постоянна для любых значений i (условие гомоскедастичности):

(i = 1,2,…, n),

где D[·] знак дисперсии;

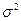- величина дисперсии.

4. Возмущения для разных наблюдений являются некоррелирован­ными:

при ,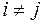

где 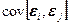- коэффициент ковариации.

Условия 3 и 4 можно объединить в одно, определяющее вид ковариа­ционной матрицы возмущений:

C _ε = =

= = = =M[ε ]= ,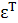

где - векторное произведение векторов;

Т – знак транспонирования матрицы;

I_n - единичная матрица n -го порядка.

5. Возмущения являются нормально распределёнными случайными вели­чинами с нулевым средним значением и дисперсие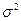й :

или .

6. Векторы объясняющих переменных (столбцы матрицы Х) линейно не­зависимы (ни один из них не может быть представлен в виде линейной комбинации других), другими словами, ранг матрицы Х равен числу её столбцов:

.

Для получения уравнения регрессии достаточно первых четырёх и шестой предпосылок. Требование выполнения пятой предпосылки необхо­димо для оценки точности уравнения регрессии и его параметров.

Традиционный метод наименьших квадратов (МНК)

Оценкой модели (1) по выборке при (i = 1,2,…, n) является уравнение:

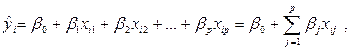(3)

которое можно представить в матричном виде:

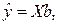(4)

где = - вектор аппроксимирующих значений зависимой переменной;

b = вектор выборочных оценок коэффициентов соответственно.

Согласно МНК, вектор неизвестных переменных параметров b выбира­ется так, чтобы сумма квадратов остатков была минимальной:

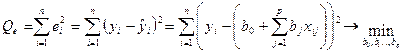, (5)

или с учётом (4) в матричной записи ( - скалярное произведение векто­ров):

. (6)

Необходимые условия экстремума (6) находятся путём приравнивания вектора частных производных: .

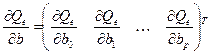Отсюда в результате приведения выражения (6) к более удобному для дифференцирования виду , с учётом известных из линейной алгебры правил вычисления производных по векторному аргу­менту 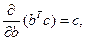(с и А – вектор и симметричная матрица соот­ветственно) получается система нормальных уравнений для определения вектора b:

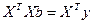(7)

Согласно предпосылке 6 КЛММР, ранг матрицы Х равен р +1. Это оз­начает, что ранг симметричной квадратной матрицы р +1-го порядка также равен р +1, она является невырожденной (её определитель не равен нулю), и существует обратная матрица такая, что произведение . Поэтому решение системы (7) можно представить сле­дующим образом:

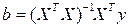. (8)

Если записать первое уравнение системы нормальных уравнений (7) в развернутом виде:

легко получить соотношение, выражающее коэффициент через осталь­ные коэффициенты и соответствующие выборочные средние:

. (9)

Дата добавления: 2015-06-04