Интегрирование нормальных систем

Одним из основных методов интегрирования нормальной системы ДУ является метод сведения системы к одному ДУ высшего порядка. (Обратная задача — переход от ДУ к системе — рассмотрена выше на примере.) Техника этого метода основана на следующих соображениях.

Пусть задана нормальная система (3.1). Продифференцируем по х любое, например первое, уравнение:

.

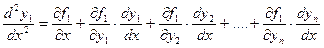Подставив в это равенство значения производных , ,…., 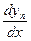из системы (3.1), получим

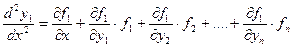
или, коротко,

.

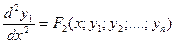Продифференцировав полученное равенство еще раз и заменив значения производных , ,…., 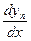из системы (3.1), получим

.

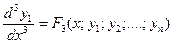Продолжая этот процесс (дифференцируем - подставляем - получаем), находим:

.

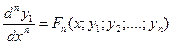Соберем полученные уравнения в систему:

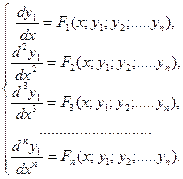(3.3)

Из первых (n -1) уравнений системы (3.3) выразим функции 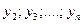через 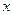, а также функцию 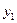и её производные 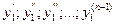. Получим:

(3.4)

Найденные значения 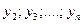подставим в последнее уравнение системы (3.3). Получим одно ДУ n -го порядка относительно искомой функции 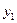: 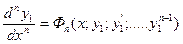. Пусть его общее решение есть

.

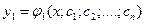Продифференцировав его (n -1) раз и подставив значения производных 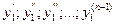в уравнения системы (3.4), найдем функции :

, ……………, .

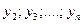Пример 3.1. Решить систему уравнений

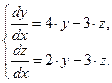
Решение: Продифференцируем первое уравнение: .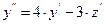

Подставляем в полученное равенство:

, .

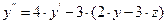Составляем систему уравнений:

Из первого уравнения системы выражаем z через у и у':

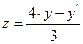. (3.5)

Подставляем значение z во второе уравнение последней системы:

,

т. е. 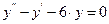. Получили одно ЛОДУ второго порядка. Решаем его 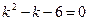, , 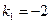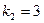и - общее решение уравнения. Находим функцию z. Значения

и

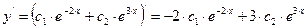
подставляем в выражение z (формула (3.5)). Получим:

.

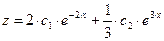Таким образом, общее решение данной системы уравнений имеет вид:

, .

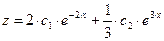Замечание. Систему уравнений (3.1) можно решать методом интегрируемых комбинаций. Суть метода состоит в том, что посредством арифметических операций из уравнений данной системы образуют так называемые интегрируемые комбинации, т. е. легко интегрируемые уравнения относительно новой неизвестной функции.

Проиллюстрируем технику этого метода на следующем примере.

Пример 3.2. Решить систему уравнений:

Решение: Сложим почленно данные уравнения: х' + у' = х + у + 2, или 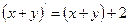. Обозначим 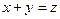. Тогда имеем .

Решаем полученное уравнение:

, , , ,

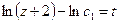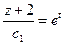или .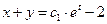

Получили так называемый первый интеграл системы. Из него можно выразить одну из искомых функций через другую, тем самым уменьшить на единицу число искомых функций. Например, 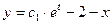. Тогда первое уравнение системы примет вид

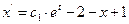, т.е. .

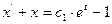Найдя из него х (например, с помощью подстановки 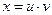), найдем и у.

Замечание. Данная система «позволяет» образовать еще одну интегрируемую комбинацию: 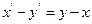, или 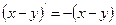. Положив

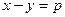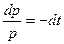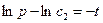, имеем: , или , , , или

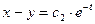. Имея два первых интеграла системы, т. е. 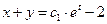и 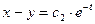, легко найти (складывая и вычитая первые интегралы), что

, .

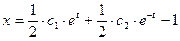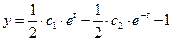Дата добавления: 2015-06-04