Интегрирование ЛНДУ второго порядка с постоянными коэффициентами и правой частью специального вида

Рассмотрим ЛНДУ второго порядка с постоянными коэффициентами, т.е. уравнение

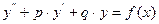, (2.10)

где р и q — некоторые числа.

Согласно теореме 2.1, общее решение уравнения (2.10) представляет собой сумму общего решения соответствующего однородного уравнения и частного решения у* неоднородного уравнения. Частное решение уравнения (2.10) может быть найдено методом вариации произвольных постоянных (п. 2.2).

Для уравнений с постоянными коэффициентами (2.10) существует более простой способ нахождения у*, если правая часть f(x) уравнения (2.10) имеет так называемый «специальный вид»:

I. 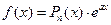или

II. .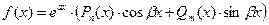

Суть метода, называемого методом неопределенных коэффициентов, состоит в следующем: по виду правой части f(x) уравнения (2.10) записывают ожидаемую форму частного решения с неопределенными коэффициентами, затем подставляют ее в уравнение (2.10) и из полученного тождества находят значения коэффициентов.

Случай 1. Правая часть (2.10) имеет вид ,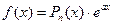

где , - многочлен степени п. Уравнение (2.10) запишется в виде

. (2.11)

В этом случае частное решение у* ищем в виде:

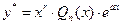, (2.12)

где - число, равное кратности а как корня характеристического уравнения
k² +pk + q = 0 (т. е. - число, показывающее, сколько раз а является корнем уравнения к² + рк + q = 0), a - многочлен степени п, записанный с неопределенными коэффициентами (i =1,2,…, n).

а) Пусть а не является корнем характеристического уравнения

k² +pk + q = 0,

т. е. 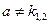. Следовательно,

, , ,

.

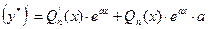После подстановки функции у* и ее производных в уравнение (2.11), сокращения на е^ах, получим:

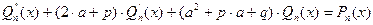. (2.13)

Слева — многочлен степени п с неопределенными коэффициентами, справа - многочлен степени п, но с известными коэффициентами. Приравнивая коэффициенты при одинаковых степенях х, получим систему (п + 1) алгебраических уравнений для определения коэффициентов .

б) Пусть а является однократным (простым) корнем характеристического уравнения k² +pk + q = 0, т. е. .

В этом случае искать решение в форме 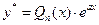нельзя, т. к. а² + pa + q = 0, и уравнение (2.13) принимает вид

.

В левой части - многочлен степени (п - 1), в правой части - многочлен степени п. Чтобы получить тождество многочленов в решении у*, нужно иметь многочлен степени (п + 1). Поэтому частное решение у* следует искать в виде (в равенстве (2.12) положить ).

в) Пусть а является двукратным корнем характеристического уравнения k² +pk + q = 0, т. е. . В этом случае а² + pa + q = 0 и 2а + р = 0, а поэтому уравнение (5.13) принимает вид .

Слева стоит многочлен степени (п – 2). Понятно, чтобы иметь слева многочлен степени п, частное решение у* следует искать в виде

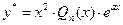, - в равенстве (2.12) положить .

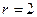Случай 2. Правая часть (2.10) имеет вид

,

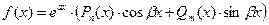где Р_п(х) и Q_m(x) - многочлены степени п и т соответственно,

а и - действительные числа. Уравнение (2.10) запишется в виде

. (2.14)

Можно показать, что в этом случае частное решение у* уравнения (2.14) следует искать в виде

(2.15)

где число, равное кратности как корня характеристического уравнения k² +pk + q = 0, 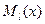и - многочлены степени l с неопределенными коэффициентами, l наивысшая степень многочленов Р_п(х) и Q_m(x), т.е. l = max(n, m).

Замечания.

1. После подстановки функции (2.15) в (2.14) приравнивают многочлены, стоящие перед одноименными тригонометрическими функциями в левой и правой частях уравнения.

2. Форма (2.15) сохраняется и в случаях, когда 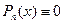или .

2. Если правая часть уравнения (2.10) есть сумма функций вида I или II, то для нахождения у* следует использовать теорему 2.2 о наложении решений.

Пример 2.2. Найти общее решение уравнения у" - 2у' + у = х - 4.

Решение: Найдем общее решение ЛОДУ у" — 2у' + у = 0. Характеристическое уравнение k² – 2k + 1 = 0 имеет корень k₁ =1 кратности 2. Значит, . Находим частное решение исходного уравнения. В нем правая часть х - 4 = (х - 4)· е^0х есть формула вида , причем а = 0, не является корнем характеристического уравнения: 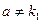. Поэтому, согласно формуле (2.12), частное решение у* ищем в виде , т. е. 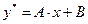, где А и В — неопределенные коэффициенты. Тогда (у*)' = А, (у*)" = 0. Подставив у*, (у*)', (у*)" в исходное уравнение, получим:

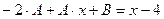, или .

Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:

,

.

Отсюда А = 1, В = - 2. Поэтому частное решение данного уравнения имеет вид у* = х - 2.

Следовательно, искомое общее решение уравнения имеет вид:

.

Пример 2.3. Решить уравнение у" - 4 у' + 13 у = 40·cosЗ х;.

Решение: Общее решение ЛНДУ имеет вид 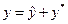. Находим решение однородного уравнения : у"-4у'+13у= 0. Характеристическое уравнение к² - 4к + 13 = 0 имеет корни , 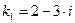. Следовательно, .

Находим частное решение у*. Правая часть ЛНДУ в нашем случае имеет вид . Так как 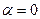, , , 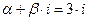- не совпадает с корнем характеристического уравнения, то . Согласно формуле (2.15), частное решение ищем в виде:

.

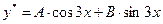Подставляем у* в исходное уравнение. Имеем: , .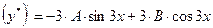

Получаем:

,

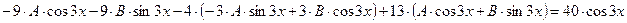или

.

Отсюда имеем:

,

.

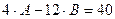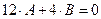Следовательно, А = 1, В = -3. Поэтому у* = cos3x - 3·sin3x. И наконец,

- общее решение уравнения.

Пример 2.4. (Для самостоятельного решения.) Для предложенных дифференциальных уравнений получить вид частного решения:

а) у"-3у' + 2у = 5 + е^х;

б) у" - 2у' + у = 2;

в) у" + 4у = sin 2х + cos 7x;

г) у" + у = 5·cos2x - х·sin2x;

д) у" - 3 у' = х² - 1 + cosx.

Ответы: а) А+х · В · е^х; б) А; в) x ·(A·cos2 x + B·sin2 x) + C·cos7 х + D·sin7 х;

г) (А · х + В) ·cos2 х + (С · х + D) ·sin 2 х; д) х ·(А · х² + В · х + С) + D ·cos х + Е ·sin х.

2.4. Интегрирование ЛНДУ n -го порядка (n > 2) с постоянными коэффициентами и правой частью специального вида

Рассмотрим линейное неоднородное ДУ n -го (n > 2) порядка

,

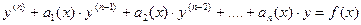где 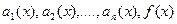- заданные непрерывные функции на 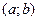. Соответствующее ему однородное уравнение имеет вид

.

Теорема 2.3 (о структуре общего решения ЛНДУ n -го порядка). Общее решение у ЛНДУ n -го порядка равно сумме частного решения у* неоднородного уравнения и общего решения соответствующего ему однородного уравнения, т. е.

Частное решение у* ЛНДУ n -го порядка может быть найдено, если известно общее решение однородного уравнения, методом вариации произвольных постоянных. Оно ищется в виде

,

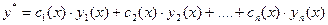где 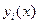, (i=1,2,…,n) - частные решения однородного уравнения, образующие фундаментальную систему.

Система уравнений для нахождения неизвестных 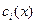имеет вид

,

,

,

…………………………………………………

.

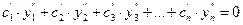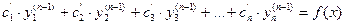Однако для ЛНДУ n -го порядка с постоянными коэффициентами, правая часть которого имеет специальный вид, частное решение у* может быть найдено методом неопределенных коэффициентов.

Метод подбора частного решения у* уравнения

,

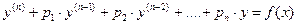где p_i - числа, а правая часть f(x) имеет специальный вид, описанный в п. 2.3 для случая n = 2, переносится без всякого изменения и на случай уравнения, имеющего порядок n > 2.

Пример 2.5. Решить уравнение y^IV - у' = 2х.

Решение: Находим :

, , , , ,

.

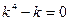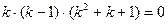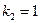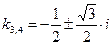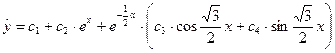Находим : , , .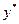

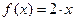
Отсюда:

, , , .

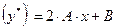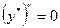Тогда: 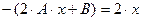. Отсюда , 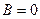и получаем: .

Следовательно, функция:

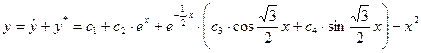
является общим решением уравнения.

Дата добавления: 2015-06-04