Методические указания к построению эпюр

Содержание контрольной работы

КОНТРОЛЬНАЯ РАБОТА № 1

Объем контрольных работ, выбор данных для них

Проведение расчетов

Для снижения трудоемкости решения и числа вычислительных ошибок рекомендуется выполнять расчеты в алгебраическом виде до конечного результата. Для получения численного решения необхо­димо в формулу подставлять числовые значения входящих в нее кон­стант и переменных в основных единицах СИ и в том порядке, в ко-

тором они расположены в алгебраическом выражении. После прове­дения необходимых математических действий результат решения должен быть записан также в основных единицах СИ. Далее он для удобства восприятия может быть выражен в кратных единицах. Ука­зание единиц измерения результата обязательно.

В расчетах на прочность, жесткость и устойчивость, как пра­вило, допускается отклонение от нормативных данных (допускаемое напряжение, допускаемые деформации, коэффициент запаса) в пре­делах ± 5 %. В связи с этим достаточным является представление чи­сел с точностью до третьей значащей цифры. Рекомендуется там, где это удобно, записывать числа с указанием десятичного порядка, на­пример: 160 000 000 – 160×10⁶; 0,0008356 – 8,36×10^-4 и т.д.

При изучении первой части курса студенты выполняют две кон­трольные работы.

Контрольная работа № 1 содержит задачи К1.1…К1.10. Кон­трольная работа № 2 – задачи К2.1…К2.10.

К каждой задаче дается десять вариантов расчетных схем и таб­лица с данными к ним.

Студенты выбирают для решения всех задач вариант расчет­ных схем, номер которого совпадает с последней цифрой индивиду­ального шифра. Данные к задачам берутся из соответствующих таб­лиц в столбце или строке, номер которых совпадает с предпоследней цифрой этого шифра. Допустим, шифр оканчивается числом 46. Расчетные схемы за­дач выбираются по варианту № 6, данные – из столбца или строки с номе­ром 4 для всех контрольных работ.

Примечание. Преподаватель может задавать расчётные схемы и исходные данные в ином порядке, но в объеме заданий, приведённых в данном пособии.

Задачи К 1.1 - К 1.10. Для десяти заданных расчетных схем (рис. 0-9, номер рисунка соответ­ствует номеру варианта задания) построить эпюры внутренних сило­вых факторов. Для пространственных рам эпюры поперечных сил Q_x, Q_y можно не стро­ить.

При построении эпюр принять т= qа², P= qa.

Данные для решения задачи взять из табл. 1.

Таблица 1

№ стро­ки	Ко­эф­фициент к	Внешние моменты	Внешние силы	Интенсивность равно­мерно рас­пределенной на­грузки
M1	M2	M3	P1	P2	P3	q1	q2	q3
		-2m	т	т	Р	Р	2Р	2q	-q	2q
	0,5	т	-2т	т	-Р	3Р	2Р	-3q	-2q	q
		m	4т	3т	2Р	Р	-1,5Р	q	-q	2q
	1,5	-т	т	2m	-1,5Р	2Р	Р	-3q	2q	q
	0,5	-3т	-m	2m	-2Р	-Р	2Р	2q	-2q	-q
		2т	т	т	3Р	-1,5Р	2Р	q	2q	2q
		-m	3т	2m	2P	2Р	Р	-q	q	q
	0,5	-2т	4m	-m	2Р	Р	3Р	-2q	2q	2q
	2,5	2т	т	-2т	-Р	Р	-3Р	2q	-3q	q
		-т	2т	0,5т	-2Р	Р	4Р	2q	q	2q

Примечание. Если значение нагрузки указано со знаком «минус», то её направ­ление на расчетной схеме следует изменить на противополож­ное, после этого нагрузка считается положительной.

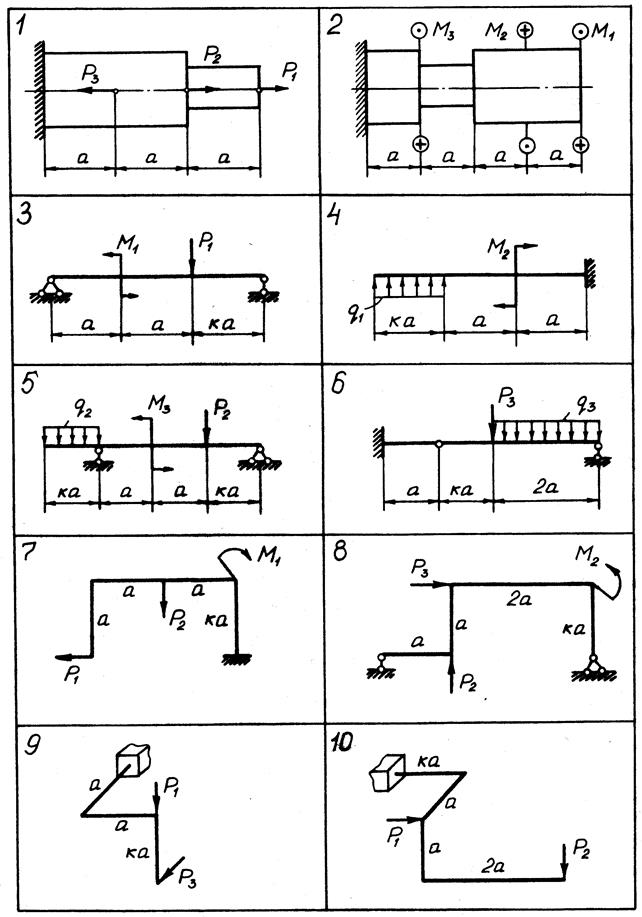
Рис. 0

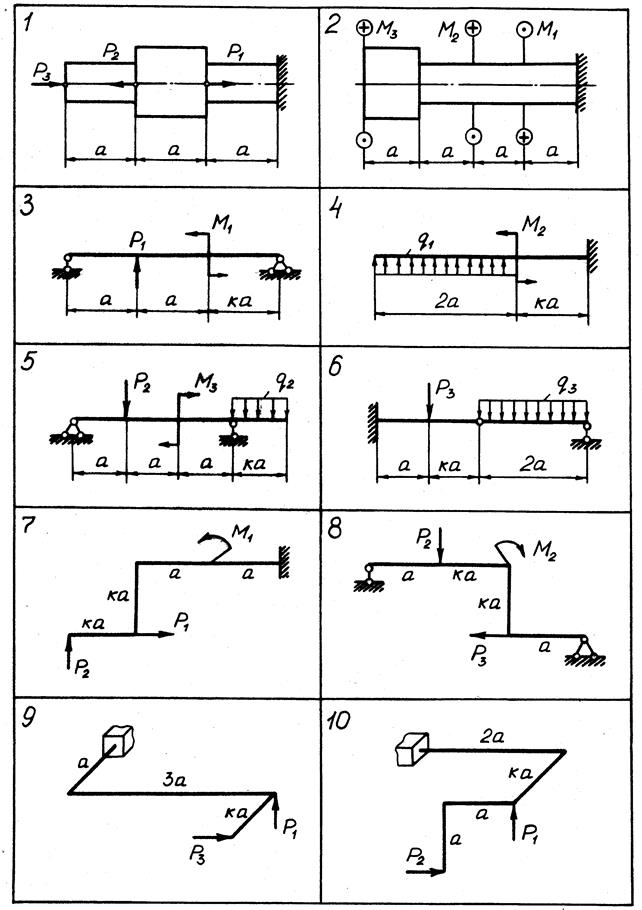
Рис. 1

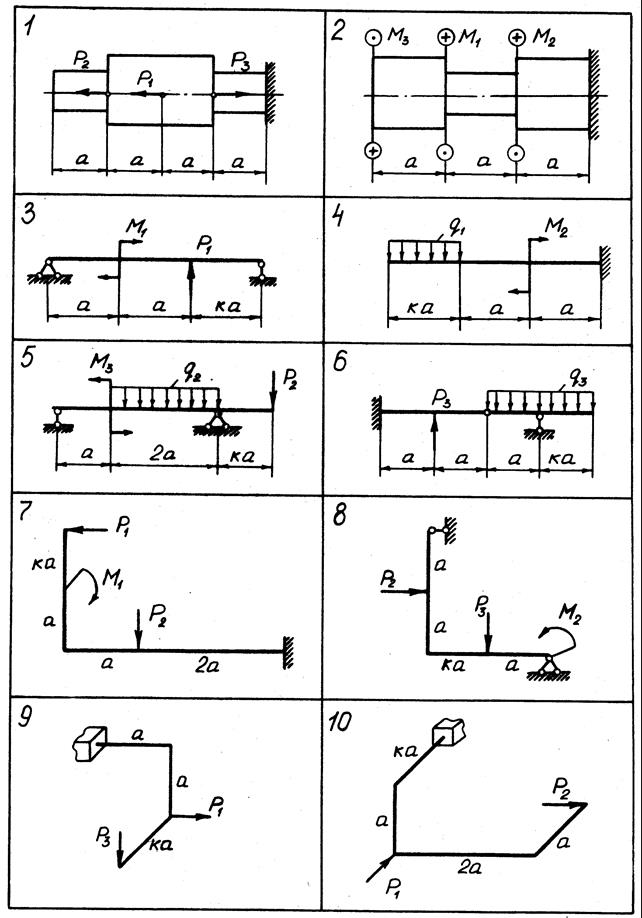
Рис. 2

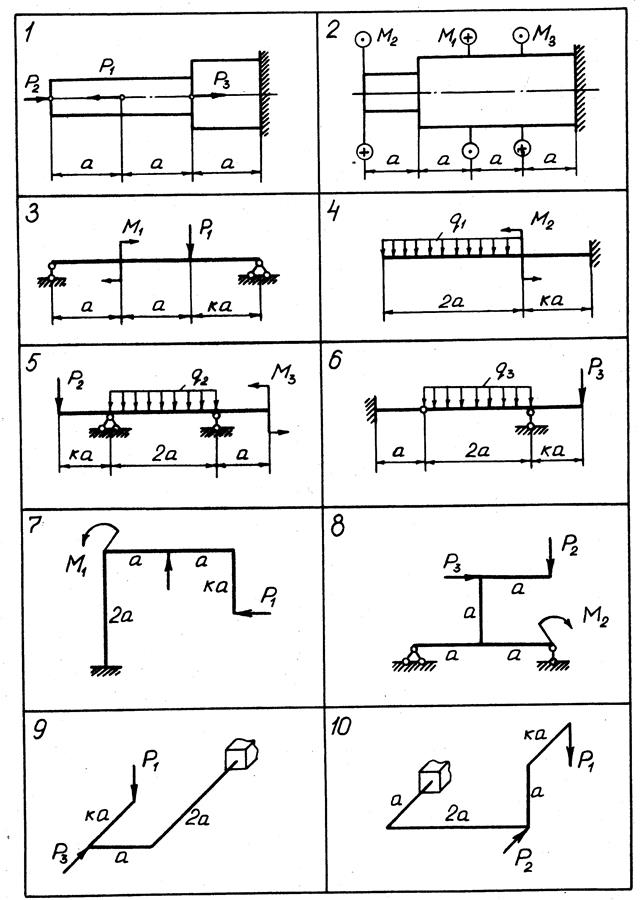
Рис. 3

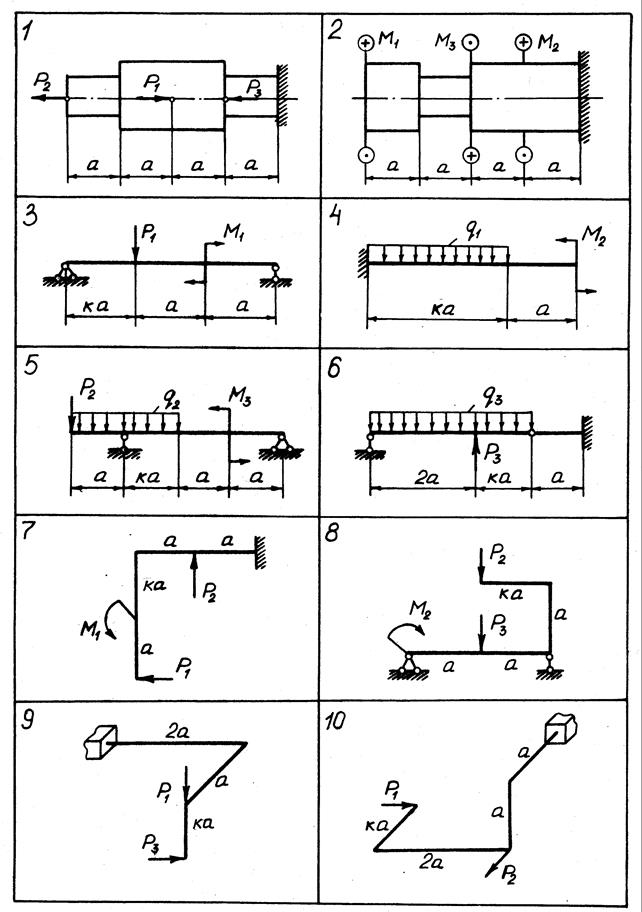
Рис. 4

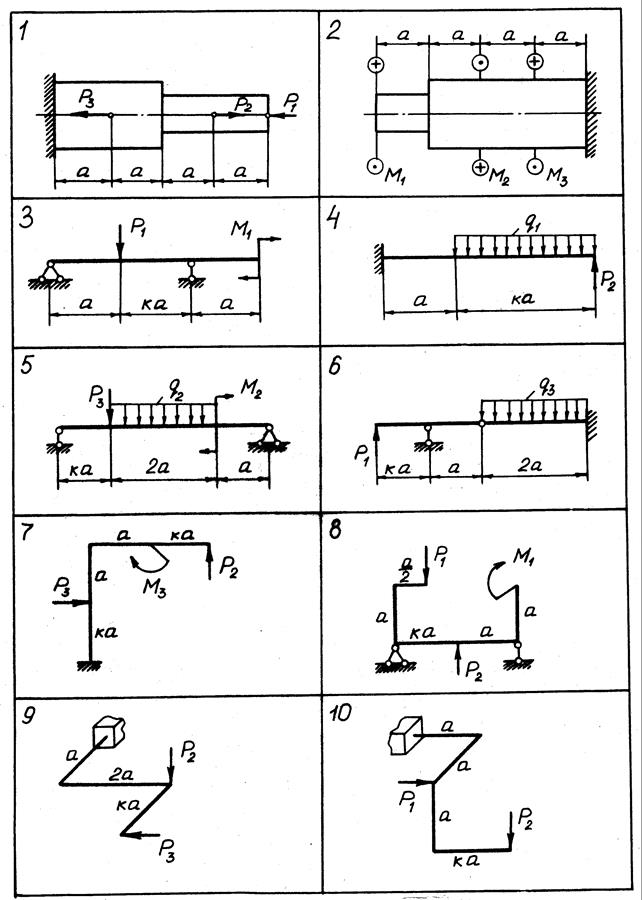
Рис. 5

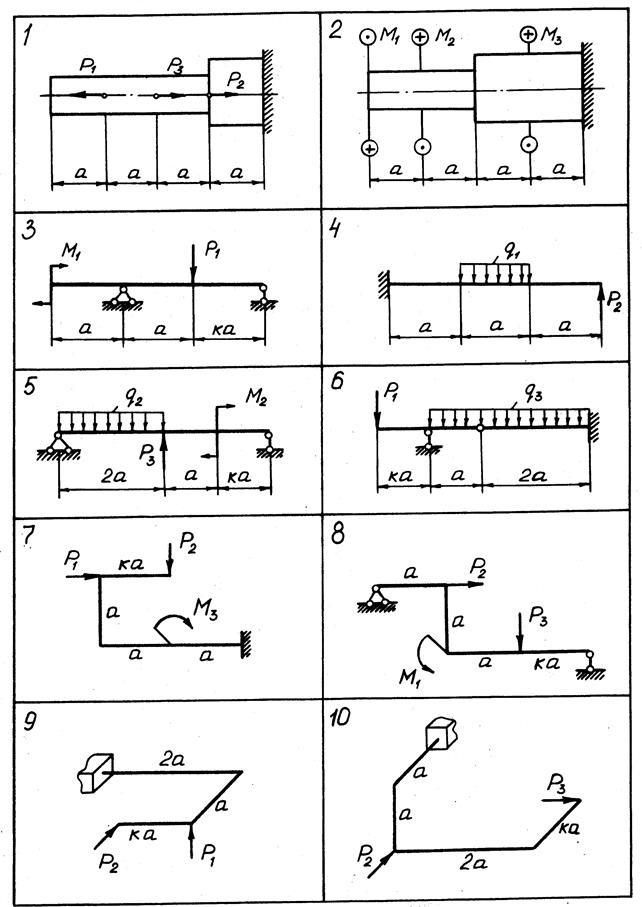
Рис. 6

Рис. 7

Рис. 8

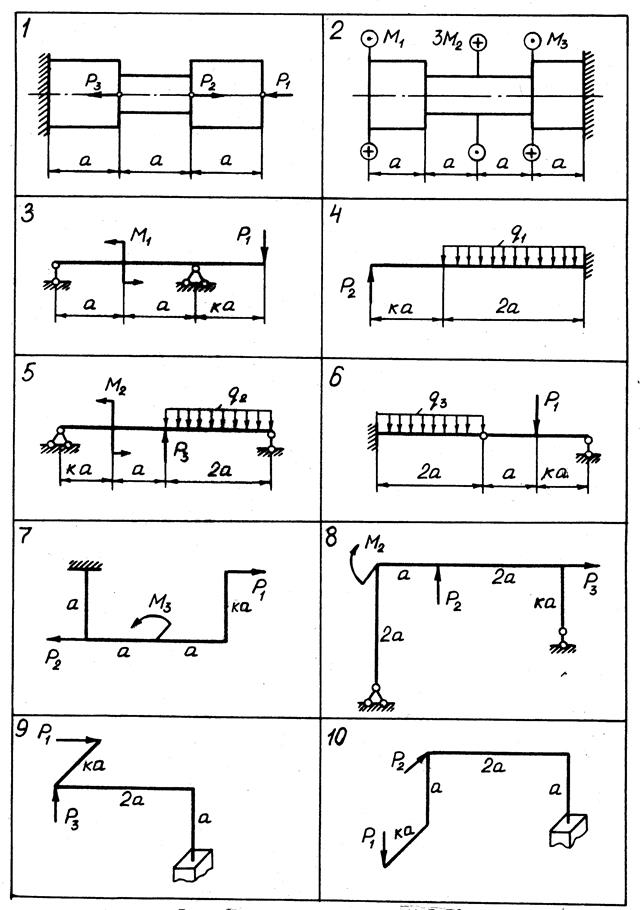
Рис. 9

внутренних силовых фак­торов

Нагрузки, приложенные к телу, деформируют его, т.е. меняют его раз­меры и (или) форму. Под действием этих нагрузок внутри тела возникают внутренние силы противодействия деформации, стремя­щиеся сохранить размеры и форму тела.

Внутренние силовые факторы – это проекции главного вектора и глав­ного момента внутренних сил на оси естественной системы ко­ординат (рис. 10). Эта система естественным образом связана с поперечным сечением бруса. Начало её расположено в центре тяжести сечения, ось z на­правлена перпендикулярно сечению по оси бруса, оси х и у распо­ложены в плоскости сечения и направлены по главным центральным осям инерции сечения (для симметричных сечений по осям симмет­рии).Внутренние силовые факторы показаны на рис.11.

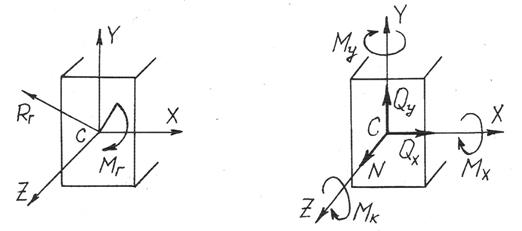
Рис. 10 Рис. 11

Естественная система Внутренние силовые

координат, главный факторы:

вектор и главный N – нормальная сила;

момент Q₁, Q₂ – поперечные силы;

М_х, М_у – изгибающие моменты

М_к – крутящий момент

Эпюры – это графическое изображение законов изменения внутренних силовых факторов по длине бруса.

Построение эпюр внутренних силовых факторов является пер­вым эта­пом любого расчета на прочность и жесткость, поэтому ос­воение алгоритма и приобретение устойчивых навыков построения эпюр являет­ся залогом ус­пешного изучения всего курса "Сопротив­ление материа­лов".

Алгоритм построения эпюр включает следующие шаги:

1. Изображение расчетной схемы в соответствии с индивиду­альным за­данием.

2. Определение опорных реакций.

3. Деление расчетной схемы на силовые участки.

4. Составление аналитических выражений для определения внут­ренних силовых факторов в произвольных сечениях участков. Вычисле­ниезначений внутренних силовых факторов на границах участков и в экстремальных точ­ках.

5. Построение эпюр.

6. Проверка правильности построенных эпюр.

Рассмотрим содержание этих шагов более подробно.*

Изображение расчетной схемы. Расчетной схемой называется формализованное изображение расчитываемого объекта, освобожденного от несущественных для данного расчета особенностей. Элементами расчетных схем являются стержни и их размеры, нагрузки и их значения, опоры.

Различают линейные, плоские и пространственные расчетные схемы.

Линейная – расчетная схема, у которой все стержни и на­грузки расположены на одной линии.

Плоская – расчетная схема, у которой все стержни и на­грузки расположены в одной плоскости.

Пространственная – расчетная схема, у которой стержни и на­грузки произвольным образом расположены в пространстве.

Расчетная схема изображается в произвольном масштабе с со­блю­де­нием соотношений между длинами участков. На расчетной схеме вмес­то ко­эффициента k, внешних нагрузок М₁, М₂, М₃, Р₁, Р₂, Р₃, q₁, q₂, q₃ указы­вается их значение, взятое из таблицы в соот­ветствии с индивидуальным за­данием.

Все нагрузки на расчетной схеме должны иметь истинное на­правление. Указание значений нагрузок со знаком «минус» не допус­кается.

___________________________________________________________________

* Примеры практического использования алгоритма даны в п. 3.3.

Определение опорных реакций. Опоры расчетной схемы обозначают буквами А, В, С и т.д. В опорах указывают реакции (силы или моменты), направление и вид которых должны соответствовать направлению и виду связей, отображен­ных на расчетной схеме в этих опорах. Силы, направленные вдоль оси бруса, обозначают бу­квой Z, перпендикулярно оси бруса – буквой Y, моменты – буквой M с индек­сами, соответствующими обозна­чению опоры, в которой возникают эти реак­ции, например Y_A, Z_A, M_A и т.д.

Для определения реакций составляют уравнения равновесия, кото­рые для плоской системы имеют вид:

; ; .

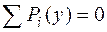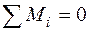С целью снижения вероятности появления ошибок рекоменду­ется ис­пользовать для определения реакций независимые уравнения равнове­сия, т.е. такие уравнения, в которые входит только одна оп­ределяемая реакция. Так, в двухопорных балках для определе­ния реакции, направленной вдоль оси балки, необходимо использо­вать уравнение , для определе­ния реакций, направленных перпендику­ляр­но оси балки, – уравнения 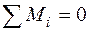относительно опорных то­чек. В плоских рамах кроме этих уравнений могут быть исполь­зо­ваны урав­нения 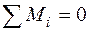относительно точек, лежащих на пересе­чении ли­ний действия двух реакций.

В расчетных схемах, имеющих внутренние шарниры, можно ис­пользовать уравнения 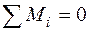относительно шарнира всех нагру­зок, расположенных по одну сторону от него.

Значение определенных реакций указывается на расчетной схеме. Если значение реакции при её определении получено со зна­ком «минус», то это оз­начает, что в действительности эта реакция имеет направле­ние, противопо­ложное указанному на расчетной схеме. Направление этой реакции на рас­четной схеме изменяют на противоположное и указывают её значение без знака «минус».

После определения всех реакций в обязательном порядке произ­во­дится проверка правильности их определения. Для этого состав­ляют такое уравнение равновесия, в которое входили бы все (или все нену­левые) найденные реакции. Для двухопорных балок уравнение, как правило, 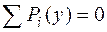, а для плоских рам 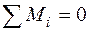относительно произ­вольной точки, не лежащей на линиях действия найденных ре­акций.

Примечание. Для расчетных схем, имеющих только одну опору (жесткую заделку), реакции в этой опоре можно не определять. При записи аналитических выражений для определения внутренних силовых факторов в этом случае учитывают все нагрузки, расположенные на расчетной схеме с одной стороны от сечения, противоположной опоре.

Деление расчетной схемы на силовые участки. С иловым участком называется часть расчетной схемы, на кото­рой за­кон изменения внутренних силовых факторов остается неиз­менным. Грани­цами силовых участков являются сечения, где при­ложены сосредо­точенные силы или моменты, начинается или конча­ется распределенная нагрузка, а также узлы рам. По этим признакам делят расчетную схему на силовые уча­стки (в дальнейшем участки). Участки нумеруют.

Составление аналитических выражений. Эпюры – это графическое изображение законов изменения внут­рен­них силовых факторов на силовых участках. Сначала составля­ются ана­литиче­ские выражения этих законов. Для этого использу­ется метод се­чений. Суть его в следующем:

- на силовом участке проводится произвольно расположенное поперечное сечение, условно рассе­кающее расчетную схему на две части;

- одначасть условно отбрасывается;

- действие отброшенной части на оставшуюся часть заменяется иско­мыми внутренними силовыми факторами, приложенными в сечении;

- для оставшейся части составляются уравнения равновесия, в ко­торые входят нагрузки, действующие на эту часть, и внутренние си­ловые факторы, приложенные в сечении. Это и будут аналитические выражения законов из­менения внутренних силовых факторов на участке. По этим выражениям строят эпюры (графики изменения внутренних сило­вых факторов).

Однако использование метода сечений в такой постановке явля­ет­ся не­оправданно громоздким и трудоёмким. Более целесообразно поступить следующим образом. На силовом участке проводят произ­вольное сечение, расстояние от него до одной из границ участка обо­значают буквой z с индексом, равным номеру участка. Для записи аналитических выражений используют следующие правила, выте­кающие из метода сечений.

Н о р м а л ь н а я с и л а в сечении равна алгебраической сумме проек­ций на ось z (ось бруса) всех нагрузок, расположенных на расчетной схеме по одну сторону от сечения.

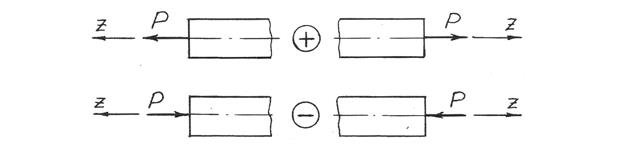Правило знаков. Если нагрузка дает проекцию, направленную от се­чения (рас­тягивающую рассматриваемый участок), то она вводится в выражение со знаком «плюс», а направленную к сечению (сжимающую) – со знаком «минус» (рис. 12).

Рис. 12.

Для удобства определения знака слагаемых при записи аналити­че­ских выражений для нормальных сил, а в дальнейшем и для попе­реч­ных сил, допускается все нагрузки, расположенные по одну сто­рону от сечения, условно переносить в начало рассматриваемого уча­стка.

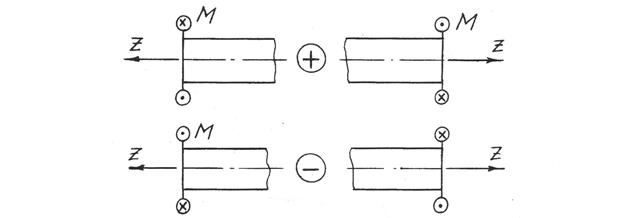
К р у т я щ и й м о м е н т в сечении равен алгебраической сумме момен­тов относительно оси бруса (оси z) всех нагрузок, рас­положенных на расчетной схеме по одну сторону от сечения.

Правило знаков. Момент, направленный против хода часовой стрел­ки, при наблюдении со стороны положительного направления оси z записывается со знаком «плюс», а направленный по часовой стрелке – со знаком «минус» (рис. 13).

П о п е р е ч н а я с и л а в сечении равна алгебраической сумме проек­ций на ось, перпендикулярную оси бруса (для плоских рас­четных схем – на ось у, для пространственных – на оси х и у), всех нагру­зок, расположенных на расчетной схеме по одну сторону от се­че­ния.

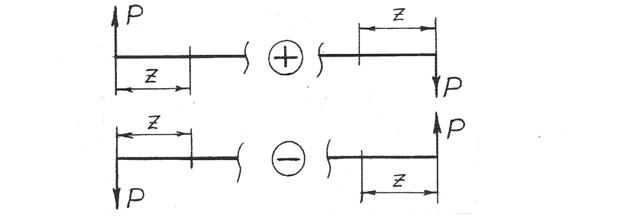Правило знаков. Если нагрузка дает проекцию, стремящуюся повернуть отсеченную часть бруса относительно сечения по часовой стрелке, то она записывается со знаком «плюс», против часовой стрелки – сознаком «минус» (рис. 14). В пространственных расчетных схемах наблюдение ведут в направлении, пер­пендикулярном плос­кости, в которой действует искомая поперечная сила (для Q_y со стороны положительного направления оси x, для Q_x со стороны положительного направления оси y).

Рис. 14

И з г и б а ю щ и й м о м е н т в сечении равен алгебраи­че­ской сумме мо­ментов относительно оси х (для М_х) или оси y (для М_y), помещенной в сечении, всех нагрузок, расположенных на расчет­ной схеме по одну сто­рону от сечения.

Для плоских расчетных схем определяется только М_х. Ось х все­гда перпендикулярна плоскости, в которой расположена расчет­ная схема, и направлена на наблюдателя, а на чертеже она превраща­ется в точку на оси бруса, через которую проведено сечение.

Правило знаков. Изгибающий момент в поперечном сечении бруса по разные стороны от оси, относительно которой он дейст­вует, вызывает напря­жения и деформации противоположных знаков. С выпуклой сто­роны бруса они растягивающие, с вогнутой – сжи­мающие (рис. 15). В подавляющем большинстве отраслей машиностроения 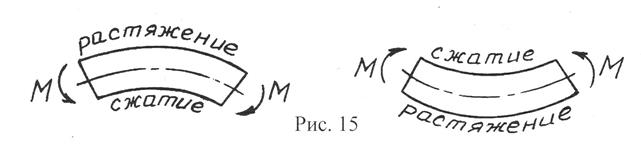принято изображать эпюры изгибаю­щих мо­ментов с сжатой сто­роны бруса (со стороны "сжатого волокна").

Таким образом, по виду эпюры автоматически определяется характер деформа­ции бруса. В различных учебниках это достигается разными приёмами.

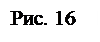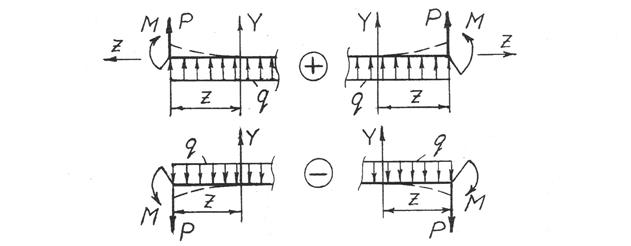
Обобщая эти приемы, предлагаем следующее универсальное правило. При записи аналитичес­ких выражений для М_х моменты на­грузок, изгибающие отсечённую часть участка в сторону положи­тельного направления оси у, считаются положительными, в противо­положную сторону – отрицательными (рис. 16). Для балок направление оси у можно указывать только один раз. Для плоских рам направление оси у указывается для каждого участка. Для М_y моменты нагрузок, изги­бающие отсечённую часть участка в сторону положительного на­правления оси х, считаются положительными, в противоположную сторону – отрицательными. В дальнейшем при построении эпюр по­ложительные ординаты откладываются в сторону положительного направления указанных осей, отрицательные – в противоположную сторону (п.3.3). Использование этого правила дает автомати­ческое построе­ние эпюр изгибающих моментов со стороны "сжа­того волокна".

Вычисление значений внутренних силовых факторов. После записи аналитических выражений вычисляют значе­ния внутренних силовых факторов на границах участков и, если необ­ходимо, в экстремальных точках. Если в аналитическое выражение не входит z (рас­стояние от границы участка до сечения), то это озна­чает, что во всех сечениях участка, в том числе и на гра­ницах, внутренний силовой фактор имеет посто­янное значение. Если в анали­тическое выражение входит z в первой степени, то это озна­чает, что внутренний силовой фактор на участке изменяется по ли­нейному зако­ну, и его эпюра изображается прямой наклонной ли­нией. Для её пост­роения вычисляют значения внутреннего силового фактора на грани­цах участка при z, равном нулю, и z, равном длине участка. Если в аналитическое выражение входит z во второй степени, то это озна­чает, что эпюра будет изображаться квадратичной параболой. Такие аналитические вы­ражения получаются для изгибающих моментов на участках, где есть равномерно распределенная на­грузка, перпенди­кулярная оси бруса. Для построения параболы в большин­стве слу­чаев достаточно значений момента на границах участка, так как из­вестно, что выпуклость параболы направлена навстречу распределен­ной нагрузке. Если внутри такого участка есть экстремальное значе­ние момента, его необходимо найти и обозначить на эпюре. Признаком наличия экс­тремума мо­мента на участке явля­ется то, что поперечная сила на границах участка имеет разные зна­ки. Известно, что поперечная сила есть первая производная от изгибающего момента, т.е. 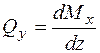; 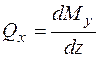, поэтому на эпюре момента экстремум будет в том сече­нии, где поперечная сила равна нулю. Для нахож­дения экстремума ранее записанное выражение для поперечной си­лы при­равнивают нулю. Из этого условия определяют z, при котором поперечная сила равна нулю, а момент имеет экстремум. Подставляя найденное значе­ние z в аналитическое выражение для момента, нахо­дят его экстре­мальное значе­ние.

Построение эпюр. Эпюры внутренних силовых факторов строят на базовых ли­ниях, повторяющих конфигурацию расчетной схемы. На базовых ли­ниях размечают границы участков. Для пространственных расчетных схем эпюры N и М_к можно строить в произволь­ных плоскостях, эпюры Q_х, Q_у, М_х, М_у строят только в тех плоскостях, в которых они действуют. На границах участков и в экстремальных точках отклады­вают с уче­том знаков вычисленные значения внутренних силовых факторов перпендикулярно базовой линии с соблюдением масштаба. Полученные точки соединяют линиями, соответствующими степени z в аналитическом выражении.

Эпюры штрихуют линиями, перпендикулярными базовой линии. На поле эпюр N, Q_х, Q_у, М_к проставляют знаки. На эпюрах М_х, М_у знаки не ставят. На границах участков и в экстремальных точках ука­зывают значения внутренних силовых фак­торов алгебраическими выражениями или числами без знака. Рядом с эпюрой в кружочке указывается условное обозначе­ние внутреннего силового фактора.

Для пространственных расчетных схем допускается строить эпюры Q_х, Q_у на одной базовой линии, так же как и эпюры М_х, М_у , М_к. В последнем случае эпюру М_к штрихуют винтовой линией.

Расчётные схемы и относящиеся к ним чертежи (эпюры и т.д.) желательно размещать на одной странице.

Проверка построенных эпюр. Построенные эпюры в обязательном порядке проверяются. Для это­го исполь­зуются характерные признаки, соответствующие кон­кретному нагружению расчет­ной схемы.При проверке эпюр попе­речных сил и изгибающих моментов ряд при­знаков вытекает из дифференциальных зависимостей при изгибе.

Правила для проверки эпюр N

1. В том сечении, где приложена сосредоточенная сила, парал­лельная оси z (оси бруса), на эпюре N должен быть скачок на величину этойсилы с учетом знака.

2. На участках, где нет распределенной нагрузки, параллельной оси z, эпюра N будет ограничена линией, параллельной базовой (N = const). Если на участке есть равномерно распределенная наг­рузка, параллельная оси бруса, то эпюра N на этом участке будет ограни­чена прямой наклонной линией.

Правила для проверки эпюр М_к

1. В том сечении, где приложен сосредоточенный момент, действующий отно­си­тельно оси z (оси бруса), на эпюре М_к должен быть скачок на величину этого момента с учётом знака.

2. Если на участке нет распределенного момента относительно оси z, то эпюра М_к будет ограничена прямой линией, параллельной базовой (М_к = const). Если на участке есть равномерно распреде­лен­ный момент относительно оси z, то эпюра М_к на этом участке будет ограничена прямой наклонной линией.

Правила для проверки эпюр поперечных сил и изгибающих

мо­ментов

Эпюры поперечных сил и изгибающих моментов проверяются попарно: Q_х и М_у, Q_у и М_х. Это обусловлено тем, что они связаны ме­ж­ду собой дифференциальными зависимостями, из которых и выте­кают ос­новные правила для проверки этих эпюр.

1. На границах расчетной схемы Q и М равны приложенным здесь внешним сосредоточенной силе и сосредоточенному моменту соответст­венно (границами расчетной схемы будем называть те её точки, от которых вся расчетная схема расположена с одной стороны).

2. В сечении, где приложена сосредоточенная сила, перпендику­лярная оси бруса, на эпюре Q будет скачок на величину этой силы с учетом её знака, на эпюре М будет излом остриём навстречу силе.

3. В сечении, где приложен сосредоточенный момент, вызы­вающий изгиб бруса, на эпюре Q никаких изменений не будет, на эпюре М будет скачок на ве­личину этого момента с учетом его знака. До скач­ка и после него ветви эпюры М будут параллельны, если в этом же сечении нет сосредоточенной силы, которая вызовет измене­ние наклона эпюры М.

4. Если на участке нет распределенной нагрузки, перпендикуляр­ной оси бруса, то эпюра Q ограничена прямой линией, параллельной базовой, эпюра М - прямой наклонной линией.

Если на участке Q = 0, то М = const, и его эпюра ограничена прямой линией, параллельной базовой.

5. Если на участке есть равномерно распределенная нагрузка, перпендику­лярная оси бруса, то эпюра Q ограничена прямой на­клонной линией, эпюра М – квадратичной параболой. Выпуклость параболы направлена навстречу распреде­ленной нагрузке. Если на границах участка Q имеет разные знаки, то на эпюре М внутри уча­стка будет экстремум.

6. Если внутри участка есть шарнир, то это никакого влияния на ход эпюр Q и М не оказывает, но на шарнире М = 0.

Дополнительное правило для проверки эпюр в рамах

Каждый узел рамы должен быть в силовом и моментном равно­весии.

Для этого составляют уравнения равновесия для узла:

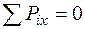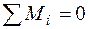; ; (для плоских рам).

Для пространственных рам:

; ; ; ; ; .

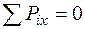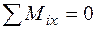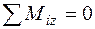При этом учитываются силы и моменты, подходящие к узлу по схо­дящимся в нём стержням, величина и направление этих сил опреде­ляются по построенным эпюрам, а также учитываются внешние силы и моменты, приложенные в узле.

Удобно использовать графическое изображение уравнений рав­нове­сия так, как это показано ниже на примере построения эпюр для плос­кой рамы (п. 3.3, рис. 22е, ж).

Дата добавления: 2015-06-30