Решение. Построить эпюры поперечных сил Q и изгибающих моментов М для балки, изображенной на рис

Пример 3

Построить эпюры поперечных сил Q и изгибающих моментов М для балки, изображенной на рис. 19а.

1. Изображаем в масштабе заданную расчётную схему балки (рис. 19а).

2. Определяем опорные реак­ции.

Освобождаем балку от внешних связей и за­меняем их действие реакциями У_А, У_В, (рис. 19б).

Составляем уравне­ния равновесия:

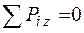, z_А = 0.

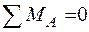, 4qa×a+M+У_B×3a-2q×3 a×2,5a=0.

.

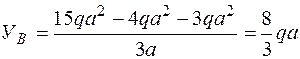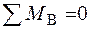, У_А×3a-4qa×2a+2q×3a×0,5a+ M =0,

откуда

.

Примечание. В уравнениях равновесия со знаком "+" записаны мо­менты, направленные против часовой стрелки относительно выбран­ных точек, как принято в курсе теоретической механики.

Знак "-", полученный для реакции У_А, означает, что она в действи­тельно­сти направлена в сто­рону, противоположную первоначаль­но выбран­ному направлению. По­этому на рис. 19б меняем направле­ние реакции У_А , теперь она направлена вниз и равна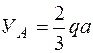

(в контрольных работах это примечание можно не за­писывать).

Проверка:

;

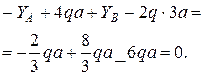
Следовательно, опорные реакции опреде­лены

верно.

На рис. 19б проставляем значения найденных реакций.

3. Разделяем расчетную схему на три силовых участка.

4. Записываем аналитиче­ские выражения для Q и M.

1-й участок: 0 ≤ z₁ ≤ a.

Распределенную нагрузку на уча­стке z₁ заменяем равнодействую­щей R_q = 2qz₁ так, как показано на рис. 20.

Тогда получаем

Q (z₁) = 2qz, Q (0) = 0, Q (a) = 2a.

М (z₁) = - 2qz₁ 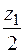, М (0) = 0, М (0) = - qa.

2-й участок: 0 ≤ z₂ ≤ 2 a,

Q (z₂) = 2q(a+z₂)- У_В, ,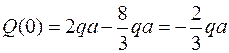

;

,

,

.

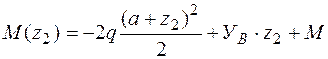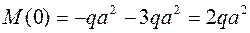Так как Q на границах участка имеет раз­ные знаки, то на эпюре момен­тов будет экстремум, найдем его.

Q (z₂) = ,

Откуда .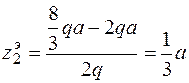

Подставляя в уравнение момента, получаем:

.

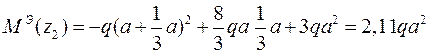3-й участок: 0 ≤ z₃ ≤ a,

Q(z₃)=-У_А= ;

М(z₃)=-У_А×z₃, М(0)=0, М(a)= .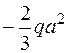

5. Строим эпюры Q и М (рис. 19в,г).

Для этого на границах участков и в экстремальной точке откла­ды­ваем по­лученные значения Q и М с учетом знаков в выбранном мас­штабе.

На эпюре моментов на втором участке точки со­единяем квадратичной параболой, выпуклость кото­рой на­прав­ляем навстречу нагрузке, остальные точки соединяем прямыми линиями.

6. Проверяем эпюры Q и М согласно правилам проверки (п. 3.2):

а) начинаем проверять границы расчётной схемы: на левой опоре в точке А действует только внешняя сила (реакция) У_А= , по­этому на эпюре Q наблюда­ется скачок на величину этой силы, а на эпюре М момент равен нулю; на правой границе в точке С нет ни силы, ни момента, поэтому и на эпюрах Q, М внут­ренние усилия равны нулю (правило 1, п. 3.2);

б) в сечении D, где приложена сосредоточенная сила Р = 4qa, на эпюре Q наблюдается скачок, равный силе (пра­вило 2, п. 3.2); на эпюре М наблюдается перегиб остриём навстречу силе (правило 3, п. 3.2);

в) в сечении В приложена сосредоточенная сила (реакция) У_В= 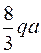и внешний момент М = 3qa², на эпюре Q наблюдается ска­чок, равный силе (правило 2, п. 3.2), а на эпюре М перегиб разорван скачком на величину приложенного здесь момента; так как в сечении действует сила, ветви эпюры М до и после скачка не параллельны (правило 3, п. 3.2).

г) правила 4, 5 (п. 3.2) мы уже использовали при построении эпюр;

д) правило 6 (п. 3.2) здесь не используется (нет внутреннего шар­нира).

Вывод. Эпюры построены верно.

Дата добавления: 2015-06-30