Контрольная работа № 2

Решение

Пример 6

Построить эпюры нормальных сил N, изгибающих М_х , М_у и кру­тя­щих М_к моментов для пространственной рамы, изображенной на рис. 24а.

Принять: Р₁ = 1,5Р; Р₂ = 2Р; Р₃ = Р.

1. Изображаем в масштабе заданную расчетную схему пространст­вен­ной рамы (рис. 24б).

2. Опорные реакции в жесткой заделке можно не определять.

3. Разделяем раму на силовые участки. Эти участки показаны на рис. 24б, их че­тыре.

В произвольном сечении каждого участка изображаем систему ко­ор­динат хуz (ось z направляем вдоль стержня).

4. Записываем аналитические выражения для нор­мальной силы N, из­гибающих моментов М_х, М_у, крутящего момента М_к.

Вычисляем значения N, М_х, М_у, М_к на границах участков.

1-й участок: 0 ≤ z₁ ≤ a,

N (z₁) = 0;

М_х (z₁) = 1,5Рz₁; М_х (0) = 0,

М_х (a) = 1,5Рa,

М_у (z₁) = 0;

М_к (z₁) = 0.

2-й участок: 0 ≤ z₂ ≤ a,

N (z₂) = -1,5Р,

М_х (z₂) = 1,5Р а;

М_у (z₂) = 0,

М_к (z₂) = 0.

3-й участок: 0 ≤ z₃ ≤ 1,5 a,

N (z₃) = 0;

М_х (z₃) = 2Р z₃, М_х (0) = 0,

М_х(1,5a) = -3Ра;

М_у (z₃) = Р z₃, М_у (0) = 0;

М_у(1,5a) = 1,5Ра;

М_к (z₃) = 0.

Рис. 24

4-й участок: 0 ≤ z₄ ≤ 2 a,

N (z₄) = Р;

М_х (z₄) = - 2Р×z₄, М_х (0) = 0,

М_х(2a) = -4Ра;

М_у (z₄) = 1,5Р×z₄ - Р×1,5а, М_у (0) = 0,

М_у (2a) = 3Ра –1,5 Ра = 1,5Ра;

М_к (z₄) = -1,5Ра – 2Р×1,5а = - 4,5Ра.

5. Строим эпюры N, М_х, М_у, М_к (рис. 24в,г,д). Для этого на границах участков на эпюрах N, М_к откладываем полу­ченные значения в произвольной плоскости с учетом знаков в выб­ран­ном масштабе; на эпюрах изгибающих моментов М_х, М_у значе­ния на границах откладываем в плоскости, перпендикулярной к оси, относи­тельно которой происходит изгиб, с учетом знаков.

6. Проверяем построенные эпюры.

4.1. Со­держание контрольной работы

Задача К 2.1

Ступенчатый стержень с площадями поперечных сечений участков F₁, F₂, F₃ нагружен осевыми силами Р₁, Р₂, Р₃, приложенными на границах или в середине участков длиной а, b, с (рис. 25). Материал стержня – сталь, допускаемое напряжение [s] = = 160 МПа, модуль упругости Е = 2×10⁵ МПа.

Требуется:

1) построить эпюры нормальных сил, напряжений и перемещений;

2) оценить прочность стержня, определить процент пере- или недо­напряже­ния.

Числовые данные взять из табл. 2.

Таблица 2

№ стро­ки	Внешние силы, кН	Длина участков, см	Площадь попереч­ных сечений, см^2
Р1	Р2	P3	b	c	a	F3	F2	F1
I

Рис. 25

Задача К 2.2

Для расчетной схемы задачи К 1.1 из условия прочности опреде­лить не­обходимые размеры поперечных сечений. Считать первый участок от за­делки квадратным, остальные – круглыми. Определить измене­ние длины по­лученного бруса. Материал стержня – дерево (сосна), допускаемое напряжение [s] = 20 МПа, модуль упругости Е = 10×10³ МПа.

Числовые данные взять из табл. 3.

Таблица 3

№ столбца		I
Внешняя сила Р, кН
Длина участков а, м	1,5	1,0	1,3	1,6	1,45	0,35	1,4	0,5	1,35	0,4

Задача К 2.3

Для стального вала круглого сечения, нагруженного скручи­вающими моментами М₀, М₁, М₂, М₃, М₄ (рис. 26) требуется:

1) определить величину и направление скручивающего момента М₀;

2) построить эпюру крутящих моментов;

3) определить диаметр вала из условий прочности и жесткости. Ок­руг­лить диаметр до ближайшего большего стандартного значения;

4) построить эпюру углов закручивания;

5) вычислить наибольшее касательное напряжение на наиболее на­гру­женном участке вала;

6) вычислить наибольший относительный угол закручивания.

Допускаемое касательное напряжение [ t ] = 50 МПа и допус­каемый относи­тельный угол закручивания [ q ] = 0,008 рад/м, модуль сдвига G = 8×10⁴ МПа.

Числовые данные взять из табл. 4.

Указание. Диаметры деталей, согласно ГОСТ 6636-69, должны соот­ветствовать ряду предпочтительных чисел...20, 21, 22, 24, 25, 26, 28, 30, 32, 34, 36, 38, 40, 42, 45, 48, 50, 52, 55, 58, 60, 65, 70, 75, 80, 90, 95, 100, 105, 110, 115, 120, 125. 130, 140, 150, 160, 170, 180,... мм.

Рис. 26

Таблица 4

№ стро­ки	Внешние моменты кН×м	Длина участков м
M1	M2	M3	M4	a	b	c
					1,0	0,6	1,9
					1,25	0,65	1,4
					1,3	0,9	0,4
					1,2	0,7	0,6
					1,4	0,8	1,6
					0,95	1,0	0,6
					1,2	1,1	0,9
					1,3	0,45	1,1
					1,7	0,6	1,2
					1,4	1,0	0,6

Задача К 2.4

Для расчетной схемы задачи К 1.2 из условия прочности опреде­лить необходимые размеры поперечных сечений. Считать первый участок вала от заделки квадратным, остальные – трубчатыми с заданным со­отношением диаметров 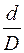. Определить угол поворота концевого се­чения вала.

Материал вала – сталь, допускаемое напряжение [τ] = 100 МПа, мо­дуль сдвига G = 8×10⁴ МПа.

Числовые данные взять из табл. 5.

Таблица 5

№ столбца		I
Внешний момент m, кН×м	0,71	0,28	0,4	0,3	0,55	0,38	0,64	0,52	0,38	0,48
Длина участков a, м	0,45	0,5	0,42	0,6	0,42	0,4	0,3	0,4	0,62	0,4
Соотношение диаметров	0,75	0,8	0,70	0,82	0,74	0,72	0,75	0,82	0,82	0,75

Задача К 2.5

Для заданного поперечного сечения (рис. 27), состав­ленного из про­стых геометрических фигур, найти положение главных цен­тральных осей инерции сечения, вычислить значения главных цент­ральных моментов инерции.

Числовые данные взять из табл. 6.

Таблица 6

№ столбца		I
a, см									6,4
b, см	10,2	6,4			8,8	8,2	8,6

Задача К 2.6

Для заданного симметричного сечения (рис. 28), состоящего из пря­мо­угольных и прокатных профилей, вычислить значения глав­ных центральных мо­ментов инерции, указать главные центральные оси.

Варианты размеров профилей приведены в табл. 7.

Таблица 7

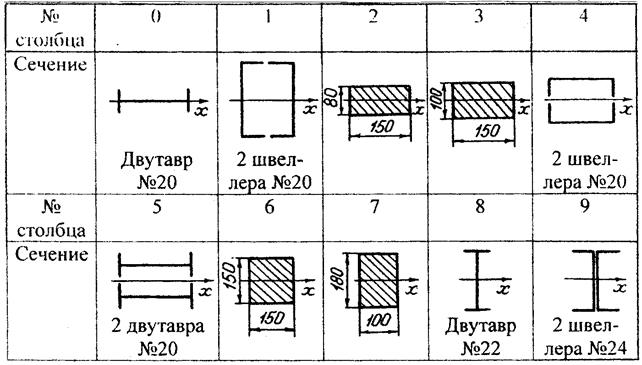
№ стро­ки	Равнобокий уголок, мм	Номер дву­тавра, швеллера	Размеры листа, мм
	45 × 45 × 5		100 × 10
I	56 × 56 × 5		120 × 10
	70 × 70 × 7		140 × 12
	80 × 80 × 8		160 × 12
	90 × 90 × 6	20 а	180 × 14
	90 × 90 × 8		200 × 16
	100 × 100 × 8	22 а	200 × 20
	100 × 100 × 10		220 × 18
	110 × 110 ×7		220 × 20
	110 ×110 × 8	24 а	240 × 20

Рис. 27

Рис. 28

Задача К 2.7

Для заданной балки (рис. 29) из условия прочности подобрать круг­лое и квадратное сечения. Сравнить их материалоёмкость. Ма­териал балки – дерево, допускаемое напряжение [s] = 12 МПа.

Принять: Р = aqa, M = bqa², a = 1,5 м.

Числовые данные взять из табл. 8.

Таблица 8

№ столбца		I
Интенсивность равномерно рас­пределен­ной на­грузки q, кН/м
Коэф­фи­ци­енты	a	1,4	0,6	1,5	2,0	1,8	0,45	1,8	0,5	1,0	1,3
b	1,6	1,0	0,75	0,8	1,25	1,0	1,25	2,0	0,75	0,9
к	1.5	0,5			1,5	0,5		0,8	1,5
Номер двутавра	24a			30a

Задача К 2.8

Для заданной балки (рис. 30) требуется:

1) проверить прочность заданного двутаврового сечения;

2) если прочность обеспечена, определить допускаемое значение ин­тенсивности распределенной нагрузки [ q ], если прочность не обес­печена, определить необхо­димый номер двутавра из условия проч­ности;

3) проверить прочность двутавра по касательным напряжениям. Если в пункте 2 опре­делялась [ q ], то при проверке учесть, что q = [ q ].

Принять: Р = aqa, M = bqa², [s] =160 МПа, [t] =100 МПа, a =2 м.

Числовые данные взять из табл. 8.

Задача К 2.9

Проверить прочность балки (рис. 31) нагруженной нагрузкой, действующей в плоскости, составляющей угол a с осью Х. Для опас­ного сечения определить положение нейтральной линии и построить эпюру нормальных напряжений. Данные взять из табл. 9 и 10.

Рис. 29

Рис. 30

Рис. 31

Таблица 9

№ строки	l, м	а	Р,кН	М, кН×м	q,кН/м	a, °	[s], МПа
		0,3 l
		0,5 l
	2,5	0,4 l
	1,5	0,6 l	2,5
	1,8	0,7 l	3,5		4,5
	2,2	0,2 l	4,2	6,5	5,5
	3,2	0,8 l	2,8	5,5	6,5
	3,5	0,55 l	1,8	4,5	7,5
	2,8	0,65 l	3,8	3,5	6,8
	2,6	0,45 l	2,2	3,8	5,6

Таблица 10

Задача К 2.10

Короткий чугунный стержень, поперечное сечение которого дано на рис. 32, сжимается продольной силой Р, приложенной в точке А. Найти допускаемую силу [ Р ] при заданных размерах сечения и допус­каемых напряжениях на сжатие [s_с] и на растяжение [s_р]. Определить положение нейтральной линии, построить эпюру нормальных напря­жений. Данные для расчета взять из табл. 11.

Рис. 32

Таблица 11

№ строки	а, см	b, см	YА, см	[sс], МПа	[sр], МПа

4.2. Методические указания к решению задач проч­ности

Дата добавления: 2015-06-30