Решение задач прочности

И жесткости при растяжении - сжатии, кручении и изгибе

Все инженерные конструкции должны быть прочными и обла­дать не­обхо­димой жесткостью.

Прочность – способность конструкции, её частей и деталей вы­пол­нять предназначенные для них функции, не разрушаясь.

Жёсткость – способность конструкции, её частей и деталей вы­пол­нять свои функции, не образуя деформаций сверх пределов, установлен­ных по ус­ловиям её эксплуата­ции.

Чаще всего условие прочности формулируется в следующем виде: макси­мальные напряжения в деталях конструкции не должны пре­вышать допускаемых напряжений для материала этих деталей. Мате­матические выражения условий прочности

– при растяжении-сжатии;

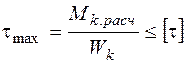– при кручении;

– при изгибе.

Здесь s, t_max, s_max – максимальные расчетные напряжения в детали; N_расч, M_к.расч, M_х.расч – максимальные по абсолютному значению нормальная сила, крутящий момент, изгибающий момент в попереч­ном сечении; F, W_к, W_х – площадь, момент сопротивления кручению и момент сопротивления изгибу поперечного сечения.

Если на детали имеются участки с разными поперечными сече­ниями, то условия прочности составляются для каждого такого уча­стка.

В инженерной практике чаще всего решаются три типа задач проч­ности:

- проверка прочности (проверочный расчет);

- определение размеров поперечных сечений, обеспечивающих проч­ность (конструкторский расчет);

- определение допустимой (максимальной) нагрузки, при которой обеспечива­ется прочность.

Алгоритм решения этих задач включает следующие шаги:

1. Выбор и изображение расчетной схемы.

2. Построение эпюр внутренних силовых факторов.

3. Определение расчетных значений внутренних силовых факторов.

4. Запись условий прочности.

5. Ответ на вопрос задачи.

Рассмотрим содержание этих шагов.*

Выбор и изображение расчетной схемы. Расчетной схемой называется формализованное изображение рас­сматри­ваемой конструкции, освобожденное от несущественных для дан­ного расчета особенностей. Расчетная схема стержневой конст­рукции содержит стержни, кото­рые изображаются своей осевой ли­нией, нагрузки, опоры, необходимые для рас­чета размеры.

Построение эпюр внутренних силовых факторов. Алгоритм построения эпюр изложен в п. 3.2.

__________________________________________________________

* Примеры практического использования алгоритма даны в п. 4.4

Определение расчетных значений внутренних силовых фак­торов. В качестве расчетного берется максимальное по абсолютной вели­чине зна­чение внутреннего силового фактора, имеющееся на его эпюре. Если стержни рас­четной схемы имеют разное поперечное се­чение, то для каждого стержня берется свое расчетное значение.

При расчете на прочность при растяжении-сжатии стержней, изго­товленных из материалов, неодинаково сопротивляющихся рас­тяже­нию и сжатию, берется два значения N_расч: максимальная рас­тяги­вающая и максимальная сжимающая.

Запись условий прочности. Если расчетная схема состоит из стержней одного сечения, то запи­сывается одно условие прочности. Если расчетная схема состоит из стержней разного сече­ния или разного размера, то записывается условие прочности для каждого стержня.

При расчете стержней, изготовленных из материалов, неодина­ково сопро­тивляющихся растяжению-сжатию, записываются отдель­ные условия прочности по растягивающим и сжимающим напряже­ниям.

Ответ на вопрос задачи. Если требуется проверить прочность конструкции, то вычисля­ются макси­мальные расчетные напряжения по формулам, состав­ляющим левую часть условий прочности, и сравниваются с допускае­мыми. Прочность конструкции будет обес­печена, если все условия прочно­сти, записанные для данной конструкции, удовлетворяются, т.е. мак­симальные напряжения не превышают допускаемых.

Если требуется определить необходимые размеры сечения или допус­каемую нагрузку, то в условии прочности вместо знака "≤" ставится знак "=".

При растяжении-сжатии ;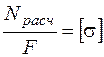

при кручении ; (4.1)

при изгибе .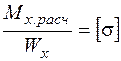

При определении размеров сечения в равенства (4.1) подставляют F, W_к, W_х , выраженные через размеры сечения, а затем разрешают их отно­сительно размеров сечения. Подставляя в полученные выраже­ния численные значения вхо­дящих в них констант и переменных и про­изводя необходимые математические действия, получают чис­ленное значение необходимых размеров сечения.

Если расчетная схема имеет участки с разными поперечными сече­ниями, то аналогичным образом определяют размеры всех уча­стков.

Если определяется допускаемая нагрузка, то в равенства (4.1) подстав­ляют N_расч, M_к.расч, M_х.расч, выраженные через внешнюю на­грузку q, Р, М. Разрешают полученные уравнения относительно внешней на­грузки и вычисляют её. Если в расчетной схеме имеются участки с разными попе­речными сечениями, то определяют допус­каемую на­грузку, исходя из условия прочности каждого участка. Та­ким образом, получают столько значений допус­каемой нагрузки, сколько участков с различными сечениями в расчетной схеме. В качестве ответа задачи берут меньшее из полученных значений допускаемой на­грузки.

Некоторые инженерные и учебные задачи прочности могут отли­чаться по своей постановке и цели от трех основных типов задач. В соответствии с этим ал­горитмы их решения также могут отличаться от алгоритма решения этих типов задач прочности.

4.2.2. Решение задач жёсткости

Здесь рассматривается решение задач жесткости при растяже­нии-сжатии и кручении. Решение задач жесткости при изгибе и сложных ви­дах нагружения бу­дет рассмотрено во второй части курса.

Условие жесткости формулируется так: перемещение в задан­ной точке или сечении конструкции не должно превышать допусти­мых по условиям эксплуатации пере­мещений этой точки или сече­ния.

Математические выражения условий жесткости:

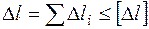– при растяжении-сжатии;

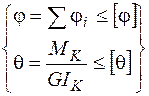– при кручении.

Здесь 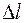– расчетное изменение длины расчетной схемы или её части; 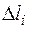– расчетные изменения длины входящих в них участков; 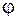– расчетный угол закручивания расчетной схемы или её час­ти; 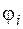– расчетные углы закручивания входящих в них участков; 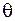– отно­си­тельный угол закручивания; – допускаемые измене­ние длины, угол закру­чивания и относитель­ный угол закручивания.

В инженерной практике чаще всего решаются три типа задач жест­кости:

проверка жесткости;

определение размеров сечения, обеспечивающих за­данную жест­кость;

определение допускаемой нагрузки, при которой обеспечива­ется жесткость конструкции.

Алгоритм решения этих задач включает следующие шаги:

1. Выбор и изображение расчетной схемы;

2. Построение эпюр внутренних силовых факторов;

3. Запись условия жесткости;

4. Определение в численном или алгебраическом виде 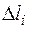, , 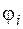вычис­ление , , .

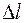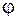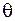Рассмотрим содержание этих шагов.

Выбор и изображение расчётной схемы и построение эпюр вы­полня­ются аналогично соответствующим шагам в алгоритме реше­ния задач прочности.

Запись условия жёсткости – содержание этого шага раскрыто в п. 4.2.2.

Определение , , , , .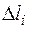

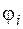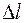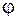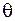На участках, где N = const, М_к = const:

, .

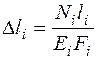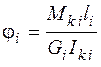На участках, где N ≠ const, М_к ≠ const:

, ,

где N(z), M_к(z) – аналитические выражения для определения N и М_к в произвольном сечении участка.

В качестве этих выражений можно использовать выражения, которые были составлены при построении эпюр.

Суммируя ∆l_i, получают выражение для ∆l, суммируя ∆ 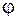_i, полу­чают выражение для 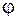. Если условие жёсткости при кручении выра­же­но через 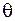, то записывают выражение для 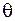. Если рас­чет­ная схема состоит из стержней одного поперечного сечения, то в ка­честве М_к в выражение для 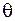подставляют максимальное по абсо­лют­ной величине значение, взятое с эпюры М_к.

Если в расчетной схеме есть участки с разными поперечными се­че­ниями, то выражение для 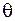составляют аналогично для каждого уча­стка.

Ответ на вопрос задачи. При проверке жесткости вычисляют численное значение ∆l, , 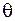и сравнивают с [ ∆l ], [ ], [ ]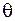. Если ∆l ≤ [ ∆l ], 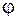≤ [ 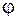], 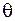≤ [ 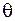], то тре­буемая же­сткость обеспечена, иначе не обеспечена.

При определении необходимых размеров или допускаемой на­грузки в условие жесткости вместо знака "≤" ставят знак "=".

Для определения размеров в полученное равенство подставляют F или I_k, выраженные через размеры сечения, затем разрешают его от­носительно размеров сечения.

При определении допускаемой нагрузки в равенство подстав­ляют N или М_к, вы­раженные через внешнюю нагрузку (если они не были уже выражены на этапе получения ∆l, 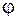, 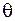), а затем разре­шают ра­венство относительно внешней на­грузки.

Примечание. Если задачи по определению размеров сечения или до­пускаемой нагрузки из условия жесткости решаются как самосто­ятельные, то после их решения в обязательном порядке необходима проверка прочности.

4.3. Методические указания к решению за­дач К 2.5, К 2.6

В задачах К 2.5 и К 2.6 требуется для сложных сечений вычис­лить значения главных центральных моментов инерции и опреде­лить по­ложение главных цен­тральных осей.

Алгоритм решения этих задач:

1. Вычерчивают сложное сечение.

2. Сложное сечение разделяют на простые составляющие части.

3. Выбирают начальные оси Х₀У₀.

4. Определяют координаты центров тяжести составляющих частей в системе координат Х₀У₀. Через их центры тяжести проводят цен­т­ральные оси составляющих частей, параллель­ные осям Х₀У₀. Вычис­ляют площади простых час­тей и их моменты инерции отно­сительно их центральных осей.

5. Определяют площадь и координаты центра тяжести всего сечения в системе координат Х₀У₀. Через центр тяжести сечения про­водят цен­тральные оси Х_сУ_с, параллельные осям Х₀У₀. Определяют моменты инерции сечения относительно этих осей.

6. Определяют главные центральные моменты инерции и по­ложение глав­ных центральных осей сечения.

Рассмотрим эти шаги более подробно.*

1-й шаг алгоритма. Сечение вычерчивается в произвольном масштабе на бумаге в кле­точку или миллиметровке. Чертеж должен занимать не менее поло­вины листа ученической тетради. На чертеже проставляют все размеры сечения, необходимые для расчета.

2-й шаг алгоритма. Простой будем называть часть сечения, для которой известны по­ло­жение центра тяжести, а также формулы для определения пло­щади и центральных мо­ментов инерции или их чи­словые значения. Для уменьшения числа составляющих частей, осо­бенно для сечений с вы­резами и отверстиями, допускается добавлять к сечению мнимые (от­сутствующие) части. В расчетах площади и моменты инер­ции мни­мых частей берутся с противоположным знаком, по сравнению со зна­ком аналогичных дейст­вительных час­тей. Простые части ну­ме­руют.

3-й шаг алгоритма. Решение можно выполнить с любыми про­извольно взятыми осями Х₀У₀ . Однако затрат труда будет меньше, если начальные оси естест­венным образом связать с сечением. Для сечений несиммет­ричных жела­тельно начальные оси на­правлять по границам сечения или простых частей. Желательно, чтобы всё сече­ние находилось в первой четверти. С целью устранения возможных ошибок рекомендуется выбирать только правую систему координат (ось У₀ направлена вверх, ось Х₀ – вправо). Для сечений симметрич­ных желательно, чтобы начальные оси сов­падали с осями симмет­рии.

4-й шаг алгоритма. При выполнении этого и пятого шага алго­ритма для снижения веро­ятности появления ошибок, повышения удобства проведения расче­тов, контроля и про­верки их правильно­сти, результаты расчетов за­носят в единую таблицу (табл. 12). Поря­док заполнения таблицы по­казан в п. 4.3.

__________________________________________________________ *Примеры практического использования алгоритма даны в разд. 4.4.

Таблица 12

Часть	хс,	ус	F	Ix	Iv	Ixy	a	b	a^2F	b^2F	abF
…
N
Сече­ние

Координаты центров тяжести определяют в системе координат Х₀У₀ с уче­том знаков. Для этого используют размеры на чертеже и зависи­мости, определяющие координаты центров тяжести простых частей. Через центры тяжести простых частей проводят их централь­ные оси, параллель­ные осям Х₀У₀. По известным формулам опреде­ляют пло­щади и моменты инерции простых частей относительно проведенных центральных осей. Если формулы для определения мо­ментов инер­ции даны для центральных осей, непараллельных осям Х₀У₀, то по­сле определения моментов инерции относительно этих осей опреде­ляют мо­менты инерции относительно центральных осей, параллель­ных осям Х₀У₀, исполь­зуя формулы для определения моментов инерции при повороте осей.

5-й шаг алгоритма. Определяют пло­щадь сечения F

,

где n – число простых частей; F_i – площадь i -ой части.

Координаты центра тяжести сечения опреде­ляют по формулам

; .

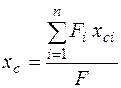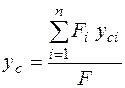Здесь x_ci, у_ci – координаты цен­тра тяжести i- ой части в системе коор­динат Х₀У₀.

В сечениях, имеющих ось симметрии, центр тяжести находится на этой оси, в сечениях, имеющих две и более осей симметрии, – на пе­ресечении осей симмет­рии.

Отмечают на чертеже центр тяжести и проводят через него цен­т­ральные оси (Х_с , У_с) сечения, параллельные осям Х₀, У₀. Вычис­ляют моменты инер­ции сечения относительно проведенных цен­тральных осей по формулам

;

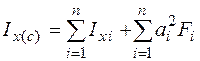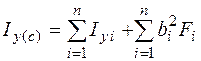; (4.2)

.

Здесь а_i= (у_сi – у_с) – расстояние между центральной осью х_с i- ой части и центральной осью Х_c сечения; b_i= (x_сi – x_с) – рас­стояние между центральной осью у_с i- ой части и цен­тральной осью У_c сечения.

Рас­стояния а_i, b_i определяются с учетом знака.

Вычисляются , , 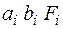для каждой части и заносятся в табл. 12. Затем находят 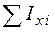, , , , 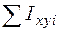, 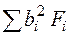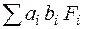путем суммирова­ния данных, записанных в соответст­вующих столбцах табл. 12. Далее находят I_x(c), I_у(c), I_xу(c) по формулам (4.2).

Дата добавления: 2015-06-30