Решение. 1. Вычерчиваем сечение в удобном масштабе

1. Вычерчиваем сечение в удобном масштабе.

2.Делим сечение на простые части: 1 – тре­угольник, 2 – полу­круг (мнимый).

3. Проводим начальные оси Х₀, У₀.

4. Готовим таблицу (табл. 13) для записи ре­зультатов расчета. Оп­ре­деляем коор­динаты центров тяжести со­ставляющих частей.

Примечание. В данном примере все расчеты выполнены в общем виде через а. Допускается, а иногда более удобно, выполнять расчеты в численном виде. Для этого на чертеже все размеры указывают в сантиметрах, затем их подставляют в рас­четные формулы, а ре­зультаты записывают в таблицу с соблюдением размерностей (см, см², см⁴).

Таблица 13

Часть	хс (а)	ус (а)	F (а^2)	Ix (а^4)	Iy (а^4)	Ixy (а^4)
I	0,25	0,333	0,375	0,0208	0,0117	-7,81×10 ^– 3
	0,0848	0,25	-0,0628	-6,29×10 ^– 4	-1,76×10 ^– 4
Сечение	0,283	0,35	0,312	0,0202	0,0115	-7,81×10 ^– 3

Окончание табл. 13

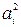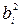Часть	ai (а)	bi (а)	F (а^4)	F (а^4)	ai bi F (а^4)
I	-0,017	-0,033	1,08×10 ^– 4	4,08×10 ^– 4	2,1×10 ^– 4
	-0,1	-0,198	-6,28×10 ^– 4	-2,46×10 ^– 3	-1,24×10 ^– 3
Сечение	---	---	-5,2×10 ^– 4	-2,05×10 ^– 3	-1,03×10 ^– 3

Треугольник ; .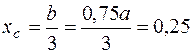

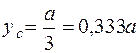Полукруг ; .

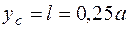Заносим эти результаты в табл. 13. Наносим на чертеж положение центров тяжести треуголь­ника и полукруга, прово­дим через них центральные оси (х₁, у₁; х₂, у₂), парал­лельные началь­ным осям Х₀ У₀ (рис. 37).

Вычисляем и заносим в табл. 13 площади и мо­менты инерции со­ставляю­щих час­тей.

Треугольник

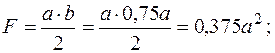
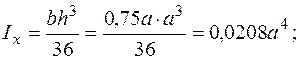
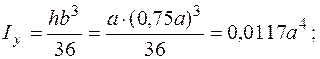
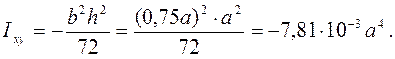
Примечание. Знак I_ху для треугольника и четверти круга зависит от положения относительно координатных осей.

Рис. 37

Полукруг (мнимый):

;

;

;

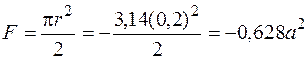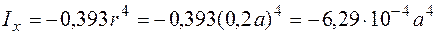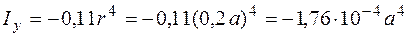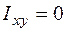, так как центральные оси полукруга являются его главными центральными осями, а относительно главных центральных осей I_ху = 0.

5. Вычисляем площадь сечения, для этого суммируем данные в столбце F, результат заносим в табл. 13.

.

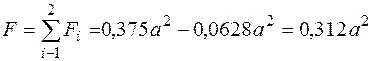Определяем координаты центра тяжести сечения и заносим резуль­таты в табл. 13:

;

.

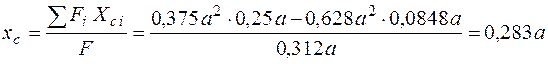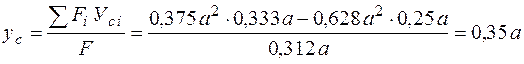Наносим на чертеж сечения положение центра тяжести и проводим через него центральные оси Х_сУ_с , параллельные начальным осям Х₀У₀.

Определяем a_i, b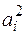_i, F_i, 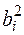F_i, a_i b_i F_i для простых частей, ре­зуль­таты заносим в табл. 13.

Треугольник

а₁ = у_с1 – у_с = 0,333 а – 0,35 а = - 0,017 а;

b₁ = х_с1 – х_с = 0,25 а – 0,283 а = - 0,033 а;

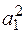F₁ = (-0,017 а)²× 0,375 а² = 1,083×10 ^{– 4} а⁴;

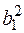F₁ = (-0,033 а)²× 0,375 а² = 4,083×10 ^{– 4} а⁴ ;

а₁b₁F₁ = (-0,017 а) (-0,033 а)×0,37 5 а² = 2,1×10 ^{– 4} а⁴.

Полукруг

a₂ = у_{с 2} – у_с = 0,25 а – 0,35 а = - 0,1 а;

b₂ = х_{с 2} – х_с = 0,0848 а – 0,283 а = - 0,198 а;

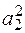F₂ = (- 0,1 а)² (- 0,0628 а ²) = - 6,28×10 ^{– 4} а⁴;

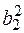F₂ = (- 0,198 а)² (0,0628 а ²) = - 2,46×10 ^{– 3} а⁴ ;

а₂b₂F₂ = (- 0,01 а) (- 0,198 а) (- 0,0628 а ²) = 1,24×10 ^{– 3} а⁴.

Определяем для сечения

S I_{x i} = 0,0208 a⁴ – 6,28×10 ^{– 4} а⁴ = 0,0202 а⁴;

S I_{y i} = 0,0117 a⁴ – 1,76×10 ^{– 4} а⁴ = 0,0115 а⁴;

S I_{x y i} = - 7,81×10 ^{– 4} a⁴ + 0 = -7,81×10 ^{– 4} а⁴;

S 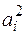F_i = 1,08×10 ^{– 4} а⁴ – 6,28×10 ^{– 4} а⁴ = - 5,2×10 ^{– 4} а⁴;

S 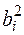F_i = 4,08×10 ^{– 4} а⁴ – 2,46×10 ^{– 3} а⁴ = - 2,05×10 ^{– 3} а⁴;

S a_ib_i F_i= 2,1×10 ^{– 4} а⁴ – 1,24×10 ^{– 3} а⁴ = - 1,03×10 ^{– 3} а⁴.

Заносим результаты в табл. 13.

Определяем центральные моменты инерции I_x(с) , I_у(с) , I_xу(с) :

I_x(с) = S I_{x i} + S 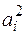F_i = 0,0202 a⁴ – 5,2×10 ^{– 4} а⁴ = 0,0197 а⁴;

I_у(с) = S I_{y i} + S 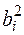F_i = 0,0115 a⁴ – 2,05×10 ^{– 3} а⁴ = 0,00945 а⁴;

I_xу(с) = S I_{x y i} = S a_ib_i F_i = -7,81×10 ^{– 3} а⁴– 1,03×10 ^–3 а⁴= -8,84×10 ^–8 а⁴.

6. Определяем главные центральные моменты инерции сече­ния

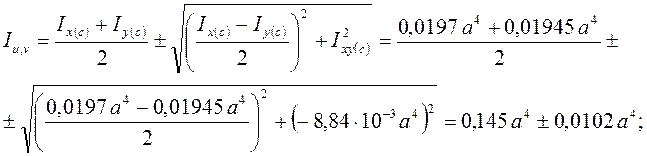
I_u = 0,0145 a⁴ + 0,0102 a⁴ = 0,0247 a⁴ = 0,0247×(0,12)⁴ = 512×10 ^{– 8}м⁴;

I_v = 0,014 5 a⁴ - 0,0102 a⁴ = 0,0043 a⁴ = 0,0043×(0,12)⁴ = 89,1×10 ^{– 8}м⁴.

Определяем угол a между осью Х_с и главной центральной осью u

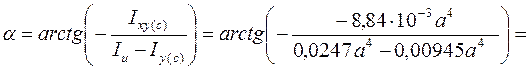
= arctg (0,433) = 23,5°.

Через центр тяжести сечения под углом a к оси Х_с на чертеже прово­дим ось u и перпендикулярно к ней ось v.

Задача К 2.6

Вычислить значения главных центральных моментов инерции, оп­ре­делить положение главных центральных осей сложного сече­ния, со­ставленного из пла­стины 200´12 мм, швеллера № 20, двух равнобо­ких уголков № 8 (80´80´8) (рис. 38).

Дата добавления: 2015-06-30