Расчёт на прочность при динамических нагрузках

Для заметок.

Расчёт элементов конструкций с учётом сил инерции.

Приближённый метод расчёта элементов на удар.

2.9.1.Во всех рассмотренных задачах предполагалось, что дей­ствующие на элемент конструкции нагрузки приложены статически, т. е. их абсолютное значение либо остается по­стоянным, либо изменяется настолько медленно, что можно пренебречь возникающими ускорениями элемента или его частей. В различных конструкциях встречаются элементы, на которые действуют динамические нагрузки. В качестве примера можно привести корпуса взлетающих ракет, быст­ро вращающиеся диски турбин, детали ковочных машин и др. При известных значениях ускорений расчет элемента конструкции с учетом возникающих сил инерции достаточ­но прост и основан на известном из теоретической механики принципе Даламбера.

Согласно принципу Даламбера, всякую движущуюся точку (или систему) можно рассматривать как находящуюся в состоянии рав­новесия, если к действующим на нее внешним силам и реакциям связей добавить силы инерции.

Сила инерции, как известно, равна произведению массы материальной точки (или системы) на ее ускорение и на­правлена в сторону, противоположную ускорению.

2.9.2. При столкновении движущихся твердых тел происходит удар. Время, в течение которого длится удар, очень мало: от десятитысячных до миллионных долей секунды. Изменение скорости движения тела за столь малое время приводит к возникновению очень больших ускорений и, следовательно, больших сил инерции. Ударные нагрузки возникают, например, в зубьях зубчатых колес при входе их в зацепление, в движущихся поступательно и вращающихся деталях ма­шин при наличии зазоров, в деталях транспортных машин при их движении по неровной поверхности и т. д. За редким исключением, когда явление удара используется в технике, например в ковочном оборудовании, ударные нагрузки вред­ны и их влияние на работу деталей машин стремятся умень­шить.

Точный расчет деталей при ударе очень сложен и связан как с трудностью определения ударных нагрузок, так и с из­менением характеристик механических свойств материалов при высоких скоростях нагружения. Применение метода расчета, основанного на использовании принципа Даламбера, невозможно, так как неизвестны значения ускорений и, следовательно, сил инерции, возникающих при столь крат­ковременном нагружении. Рассмотрим приближенный ме­тод расчета на прочность при ударе, основанный на сле­дующих допущениях.

1. Материал элемента конструкции при ударном нагру­жении следует закону Гука, при этом модуль упругости имеет то же значение, что и при статическом нагружении.

2. Отсутствует упругий отскок ударяющего тела от уда­ряемого. После соприкосновения ударяющее тело как бы «прилипает» к ударяемому и они движутся вместе.

3. Масса конструкции, воспринимающей действие ударной нагрузки, мала по сравнению с массой ударяющего груза, т.е. система рассматривается как невесомая. при расчете на удар можно пренебречь.

4. Кинетическая энергия ударяющего тела полностью пе­реходит в потенциальную энергию упругой деформации рас­считываемого элемента конструкции.

Пусть твердое тело весом G падает с некоторой высоты h на упругий элемент конструкции, например на стержень или балку (рис. 2.9.1.). Силу, с которой твердое те­ло ударяет по элементу конструкции, назовем динамической нагрузкой 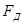. Очевидно, значение этой нагрузки больше ве­са ударяющего тела в некоторое число раз, которое назовем динамическим коэффициентом :

.

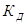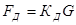На основании закона Гука перемещение 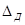, вызванное в элементе динамической нагрузкой 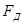(укорочение стержня, прогиб балки и т.д.), также в 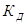раз больше перемещения 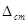, вызванного статическим приложением веса падающего тела:

.

В данном случае динамический коэффициент вычисляется по формуле

.

На основании закона Гука напряжения в элементе конст­рукции при ударе определим из соотношения

.

где — напряжение, возникающее в элементе конструк­ции при статическом приложении к нему веса падающего твердого тела.

Заметим, что в частном случае при высоте падения тела , т. е. при мгновенном приложении нагрузки 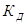=2. Следовательно, напряжения и деформации в элементе при мгновенном приложении нагрузки вдвое больше, чем при статическом ее действии.

Рассмотрим случай ударного нагружения, когда ударяю­щее тело массой т движется горизонтально со скоростью v. Упругую систему условно изобразим в виде пружины (рис. 2.9.2.). Перемещение в упругой системе при ударе силой 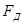равно .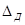

Как и ранее, значения динамической нагрузки 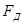и вызванного ей перемеще­ния 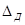системы в 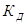раз больше соответ­ствующих статических значени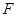й и :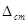

; .

В данном случае динамический коэффициент вычисляется по формуле

.

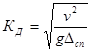Определение напряжений и деформаций в элементах конструкций при ударе сводится к их определению при статическом приложе­нии веса ударяющего тела в направлении его движения и вычисле­нию динамического коэффициента.

Анализ формул для определения динамического коэффи­циента показывает, что при увеличении 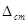, т. е. уменьше­нии жесткости системы, уменьшается значение 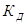а сле­довательно, уменьшается значение . В связи с этим для смягчения ударов уменьшают жесткость системы, применяя различные пружины, рессоры и т. д.

Дата добавления: 2015-06-30