Уравнение Эйлера движение идеальной жидкости

При выводе уравнений Эйлера предполагается, что вместе с потоком внутри него движения бесконечно малый параллелепипед массой 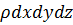; в заключительной части вывода на это произведение были поделены все слагаемые каждого уравнения – это отражает тот факт, что от объема параллелепипеда и от длины его ребер результат не зависит, но сам параллелепипед должен оставаться бесконечно малым.

Таким образом, каждый член уравнения Эйлера представляет силу, действующую на некоторую частицу жидкости, а после деления на массу частицы получает размерность ускорения.

2. Общие замечания об интегрировании уравнений движения.

Каждое из уравнений (…) представляет собой проекцию на одну из осей координат уравнения движения

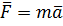
где 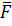- результирующая внешних сил, действующих на элементарный параллелепипед (уравнения записаны в том виде, который получен после деления обеих частей уравнения движения на массу элементарного параллелепипеда ).

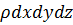Для лучшего понимания дальнейшего приведения некоторые элементарные сведения из механики.

При интегрировании уравнения 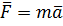возможно найти интеграл от силы по времени, при этом

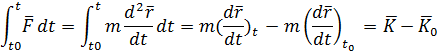
т.е. интеграл от силы по времени, называемый импульсом силы, равен полному изменению количества движения.

Интеграл от силы по пути. Работа, производимая силой 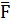при перемещении массы m на бесконечно малый отрезок d 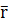, определяется в общем случае как скалярное произведение 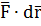, то есть выражается интегралом

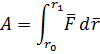
Подставляя в последнее выражение для работы вместо 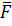равный ему вектор 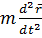и переходя к интегрированию по времени с помощью соотношения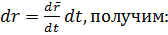

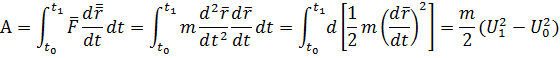
Последнее выражение возможно сформулировать так: работа силы на данном пути равна разности кинетических энергий в конечном и начальном состоянии.

Дата добавления: 2015-07-02