Интеграл Бернулли

Интегрируем уравнение Эйлера при следующих допущениях:

1. Движение установившееся.

2. Массовые силы, действующие на жидкость имеют потенциал.

3. Жидкость баротропна, т.е.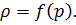

При установившемся движении линии тока совпадают с траекториями частиц. Поэтому, например, проекция 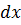перемещения частицы жидкости 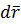вдоль элементарной струйки за время 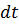равна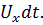

С целью интегрирований уравнений движения идеальной жидкости

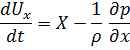
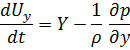
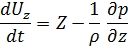
Умножим на 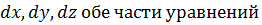(Д) соответственно и сложим отдельно левы и правые части.

Левую часть, полученную в результате сложения, преобразуем так:

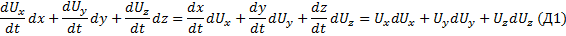
Заметим для дальнейших преобразований следующее:

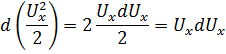
Тогда левая часть будет иметь вид:

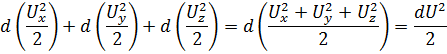
Так как движение установившееся, то давление не зависит от времени:

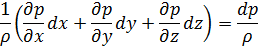
Так как массовые силы имеют потенциал, то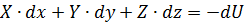

Если массовой силой является сила тяжести, то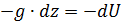

В результате преобразованное выражение принимает вид:

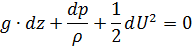
В частности, для несжимаемой жидкости :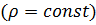

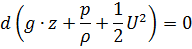
Производя формальное интегрирование последнего выражения получим:

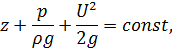
т.е. сумма трех слагаемых в левой части последнего равенства (интеграла Бернулли) сохраняет постоянное значение вдоль элементарной струйки.

Если на данной элементарной струйке выбрать два сечения, то для них возможно записать:

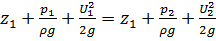(Y1)

Это равенство называется уравнением Бернулли для элементарной струйки идеальной жидкости. (так как на сечение элементарной струйки не накладывается никаких ограничений, его возможно выбрать прямоугольным со сторонами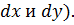

Так как скорость и давление по течению элементарной струйки не меняются, то уравнение (Y1) справедливо для линии тока.

Несмотря на то, что удельная энергия жидкости в элементарной струйке имеет конечное значение 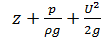, ее полная энергия:

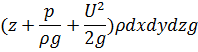
в любом сечении бесконечно мала.

Дата добавления: 2015-07-02