Характеристики регулярного волнения

Наиболее изучена качка корабля на регулярном волнении. Это сложилось исторически. К тому же расчеты качки на регулярном волнении служат основой для расчета качки на нерегулярном и прибойном волнении.

В расчетах качки обычно используется описание линейных волн. При этом считается, что амплитуды волн малы по сравнению с их длинами, скорости и ускорения частиц воды в волнах малы.

Система координат 0°x°h°z° для описания волн изображена на рис. 2.1. Ось 0°x° направлена параллельно скорости бега волн 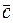, ось 0°h°- параллельно фронту волн, ось 0°z° - вертикально вниз. Плоскость 0°x°h° - невозмущенная поверхность воды.

Рис. 2.1. Система координат для описания характеристик волнения

Для дальнейшего необходимы следующие характеристики:

1. Уравнение волновой поверхности

z°_в = r₀ cos (kx° - w t), (2.1)

где r₀ - амплитуда волны, в то же время - это полувысота волны, т.е.

r₀ = 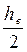, (2.2)

а также радиус орбитального движения частиц воды, находящихся на поверх-ности;

h_в - высота волны - максимальное расстояние по вертикали между крайними точками на вершине и подошве волны;

k = 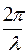- (2.3)

волновое число или частота формы, характеризующая количество волн на единицу длины;

l - длина волны - расстояние по горизонтали между двумя соседними точками, находящимися в одной фазе;

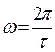- (2.4) частота волны, характеризующая количество волн, проходящих относительно заданной вертикали в единицу времени;

t - период волны, т.е. время одного полного колебания уровня воды относи-тельно заданной вертикали.

2. Между волновым числом и частотой волны существует связь, известная из теории линейных волн,

k = 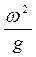. (2.5)

Из этой формулы можно определить зависимость между длиной волны и периодом. Подставив (2.3) и (2.4) в (2.5), получим

l = 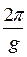t² » 1,56 t² . (2.6)

Тогда

t = » 0,8 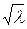. (2.7)

3. Между высотой волны и длиной существует статистическая связь, которая описывается формулой Циммермана.

h_в = 0,17 l 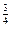. (2.8)

4. Крутизна волны

К = 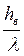(2.9)

выражается в виде дроби, в числителе которой стоит 1, а в знаменателе - число, показывающее, во сколько раз длина волны больше высоты (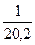; ; 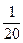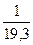и т.д.). Обычно в стандартных расчетах качки сооружений на морском волнениипринимается К = 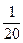, но на озерах, водохранилищах и внутренних морях волны более крутые, и значения К могут достигать .

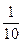5. Угол волнового склона (другая характеристика крутизны) - угол между касательной к волновой поверхности и осью 0°x°.

Как мы знаем, тангенс угла наклона касательной - производная, т.е.

a» tg a = = - kr₀ sin (kx⁰ - w t). (2.10)

Величина

a₀ = kr₀ - (2.11)

амплитуда угла волнового склона или максимальный угол волнового склона.

Подставим (2.3) в (2.11) и получим

a₀ = 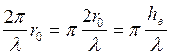, (2.12)

т.е. a₀ =p К - аналог крутизны, измеряемый в радианах.

Можно получить a₀ в градусах, умножив a₀ в радианах на 57,3⁰:

a₀ = 180⁰ 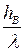. (2.13)

6. Скорость волны (скорость перемещения фронта волн) определяется из формулы

с = 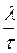, (2.14)

поскольку действительно одна длина волны проходит за один период. С уче-том (2.7)

с» 1,25 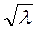. (2.14¢)

7. Радиус орбитального движения частиц воды, находящихся на глубине z⁰ , равен

r_z = r₀ e^{- kz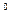} . (2.15)

8. Давление в волне можно определить по формуле, известной из теории линейных волн,

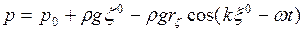, (2.16)

где p₀ - атмосферное давление, 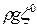- гидростатическое давление на глубине z⁰,

Dp_в = - rg 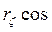(kx⁰ - w t) - (2.17)

волновая добавка к давлению в волне. Именно Dp_в вызывает качку судна. Если волновое движение отсутствует, Dp_в = 0. На поверхности волны

Dp_в = - rg 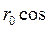(kx⁰ - w t). (2.18)

9. Энергия плоской волны

Е = 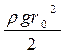. (2.19)

Эта энергия погонная, т.е. приходящаяся на 1 м ширины волны. Как было отмечено выше, по направлению оси 0⁰h⁰ волна распространяется в бесконечность.

Дата добавления: 2015-07-02