Коэффициенты затухания

СОБСТВЕННЫЕ ЧАСТОТЫ И ПЕРИОДЫ КАЧКИ КОРАБЛЯ.

КАЧКА КОРАБЛЯ НА ТИХОЙ ВОДЕ.

На тихой воде в правых частях уравнений (3.8) получаются нули, так как возмущающие силы и моменты отсутствуют.

Предположим, что в какой-то момент времени на корабль подействовало внешнее возмущение. После прекращения его воздействия корабль будет испытывать качку. Ввиду отсутствия восстанавливающих сил дополнительные виды качки будут представлять собой апериодические движения (смещения), т.е. не представляют с точки зрения качки практического интереса.

Уравнения основных видов качки будут

(3.9)

Разделим все члены уравнений на соответствующие первые коэффициенты:

(3.10)

Введем новые обозначения:

а) коэффициенты затухания соответственно вертикальной, бортовой и килевой качки

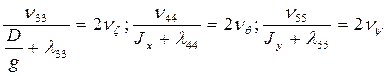; (3.11)

б) собственные частоты соответственно вертикальной, бортовой и килевой качки

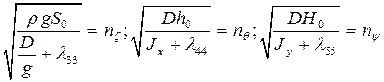. (3.12)

С этими частотами связаны периоды вертикальной, бортовой и килевой качки соответственно

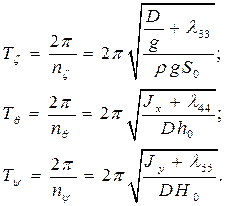(3.13)

Таким образом, уравнения качки запишутся в приведенной (удобной для решения) форме:

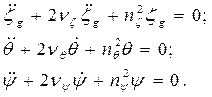(3.14)

Эти уравнения описывают затухающие колебания. Для наиболее интерес-ного случая бортовой качки решение будет иметь вид (рис. 3.5):

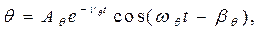(3.15)

где А_q - начальная амплитуда; 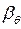- фаза, характеризующая отстояние макси-мальной амплитуды от начала колебаний; 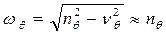- частота качки корабля на тихой воде (здесь учитывается, что ).

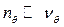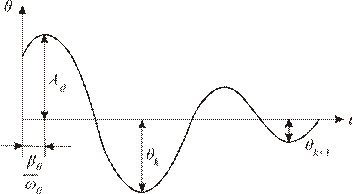
Рис. 3.5. Запись затухающих бортовых колебаний на тихой воде

Дата добавления: 2015-07-02