
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Малых размеров на волнении
|
|
|
|
ВЫВОД УРАВНЕНИЙ КАЧКИ КОРАБЛЯ БЕСКОНЕЧНО
Для корабля бесконечно малых размеров возмущающие силы легко выводятся с использованием принципа относительного движения.
Рассмотрим вначале вертикальную качку (рис. 3.6). корабль переместится от начального положения на величину  со скоростью
со скоростью 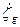 и ускорением
и ускорением  , но за это время волновая поверхность переместится на расстояние
, но за это время волновая поверхность переместится на расстояние  cо скоростью
cо скоростью 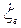 и ускорением
и ускорением  .
.
Соответственно все гидромеханические силы будут зависеть от относи-тельных параметров качки. Тогда уравнение качки на тихой воде можно записать в форме Лагранжа
 . (3.31)
. (3.31)
Перенесем часть членов в левую часть уравнения
 . (3.32)
. (3.32)
Если подставить  из (3.30), а также
из (3.30), а также 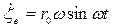 и
и  , получим уравнение вертикальной качки корабля беско-нечно малых размеров на волнении
, получим уравнение вертикальной качки корабля беско-нечно малых размеров на волнении
 (3.33)
(3.33)
В левой части уравнения стоят члены, описывающие качку на тихой воде, в правой - члены, зависящие от характеристик волнения - возмущающие силы. Если волн нет, в правой части будет 0.
Получить возмущающие силы можно также, закрепив корабль таким обра-зом, чтобы ограничивалась вертикальная качка, а другие виды качки не ограничивались. Силы, необходимые для удержания такого закрепленного корабля, и будут возмущающими силами.
Первая составляющая, пропорциональная перемещению  имеет гидро-статическую природу. Она называется крыловской силой. Получить ее можно по гипотезе Крылова о том, что корабль своим присутствием не иcкажает набегающую волну, т.е. является как бы проницаемым. Эту силу также называют главной, так как для обычных кораблей на ее долю приходится до 80% суммарной возмущающей силы.
имеет гидро-статическую природу. Она называется крыловской силой. Получить ее можно по гипотезе Крылова о том, что корабль своим присутствием не иcкажает набегающую волну, т.е. является как бы проницаемым. Эту силу также называют главной, так как для обычных кораблей на ее долю приходится до 80% суммарной возмущающей силы.
Вторая и третья составляющие называются дифракционными силами. Они учитывают искажение поля давлений в волне из-за присутствия корабля. Сила 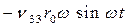 пропорциональна коэффициенту сопротивления (демпфиро-вания) и называется демпфирующей частью дифракционной составляющей, а сила
пропорциональна коэффициенту сопротивления (демпфиро-вания) и называется демпфирующей частью дифракционной составляющей, а сила  называется соответственно инерционной частью дифракционной составляющей.
называется соответственно инерционной частью дифракционной составляющей.
При выводе уравнений бортовой качки корабля проводим аналогичные рассуждения (рис. 3.7). Корабль наклоняется на угол  с угловой скоростью
с угловой скоростью 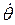 и угловым ускорением
и угловым ускорением  . За это время волновая поверхность наклоняется на угол
. За это время волновая поверхность наклоняется на угол 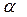 с угловой скоростью
с угловой скоростью 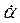 и угловым ускорением
и угловым ускорением  . Относительное перемещение корабля будет происходить на угол
. Относительное перемещение корабля будет происходить на угол 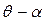 с угловой скоростью
с угловой скоростью  и угловым ускорением
и угловым ускорением 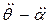 .
.
Уравнение Лагранжа для бортовой качки можно записать в виде:
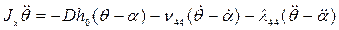 . (3.34)
. (3.34)
Перенесем часть членов уравнения в левую часть
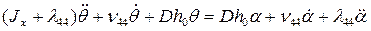 . (3.35)
. (3.35)
|
Рис. 3.6. Определение возмущающих сил при вертикальной качке
Подставим в (3.35)  ,
,  и получим уравнение бортовой качки корабля бесконечно малых размеров
и получим уравнение бортовой качки корабля бесконечно малых размеров
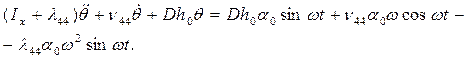 (3.36)
(3.36)
В правой части уравнения (3.36) стоят следующие составляющие возму-щающего момента:
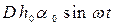 - крыловская (главная) составляющая возмущающего момента;
- крыловская (главная) составляющая возмущающего момента;
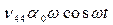 - демпфирующая часть дифракционной составляющей;
- демпфирующая часть дифракционной составляющей;
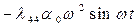 - инерционная часть дифракционной составляющей.
- инерционная часть дифракционной составляющей.
Получить возмущающий момент можно, закрепив корабль так, чтобы он имел возможность перемещаться вертикально, но не мог совершать угловых перемещений.
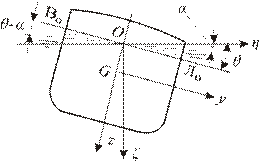
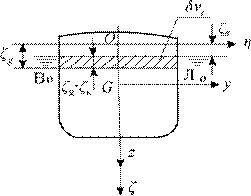
Рис. 3.7. Определение возмущающих моментов при бортовой качке
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 421; Нарушение авторских прав?; Мы поможем в написании вашей работы!