Стоящего на тихой воде

ВЫВОД УРАВНЕНИЙ ПРОДОЛЬНОЙ КАЧКИ КОРАБЛЯ,

ЛИНЕЙНАЯ ТЕОРИЯ ПРОДОЛЬНОЙ КАЧКИ КОРАБЛЯ

Условия продольной качки корабля на волнении существенно отличаются от условий его бортовой качки по следующим причинам:

а) невозможно применить допущение о малости размеров корабля по сравнению с размерами волны, поэтому совершенно недопустимо пренебрежение кривизной волны на протяжении длины корабля;

б) велико взаимное влияние вертикальной и килевой качки друг на друга, так как собственные частоты этих видов качки весьма близки;

г) продольная качка в гораздо большей степени зависит от скорости хода корабля, чем бортовая качка в положении лагом.

При составлении уравнений продольной качки используем следующие основные допущения:

1) справедлив принцип суперпозиции (наложения) действующих на корабль сил. Согласно этому принципу отдельные категории сил не влияют друг на друга и их можно просто суммировать. Принцип суперпозиции достаточно точен при малых перемещениях, скоростях и ускорениях корабля, также при действии малых волн;

2) справедлива гипотеза плоских сечений. Результирующие гидроди-намических сил и моментов, действующих на различные участки длины корабля неодинаковы. Для приближенного их суммирования мы предполагаем, что плоскости действия всех видов гидродинамических сил параллельны плоскости мидельшпангоута, т.е. силы действуют в плоскостях шпангоутов. Тогда главный вектор и главный момент действующих сил могут быть получены путем суммирования этих сил и моментов, вычисленных для элементарных отсеков;

3) перемещения, скорости и ускорения корабля малы, так что можно пренебречь их произведениями;

4) обводы корабля в пределах изменения осадки прямобортны.

Для вывода уравнений продольной качки корабля, стоящего на тихой воде, возьмем элементарный отсек длиной dx на расстоянии х от плоскости Gyz в какой-то момент времени t, как это показано на рис. 4.1. Смещение ЦТ корабля будет равно 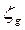и корабль повернется на угол . Отсек будет участвовать в переносном движении вместе с ЦТ и в относительном движении относительно оси Gy, проходящей через ЦТ. Поскольку качка мала, можно приближенно считать, 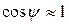и .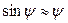

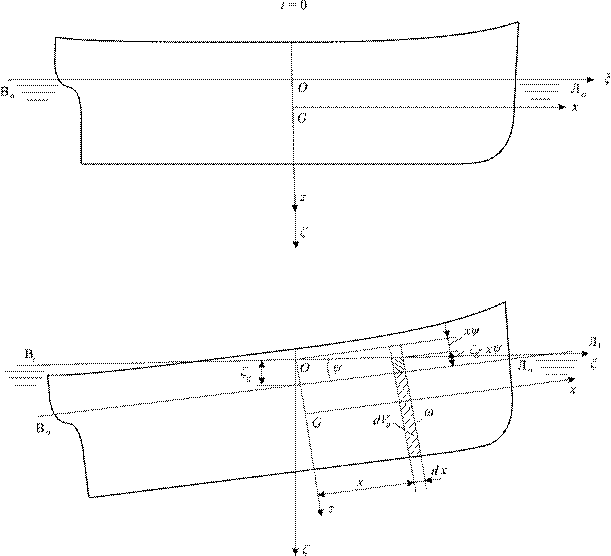
Рис. 4.1. Перемещение элементарного отсека при продольной качке

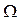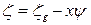Объем отсека по начальную ватерлинию будет равен , где - объем погруженной части шпангоута. Кроме этого объема под водой находится еще объем . Его высота равна , а величина - . Тогда сила поддержания, действующая на отсек, будет равна

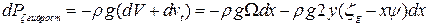. (4.1)

Скорость перемещения отсека и ускорение равны соответственно 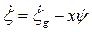и 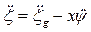, тогда сила сопротивления движению отсека будет

, (4.2)

где 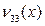- коэффициент сопротивления вертикальной качке плоского шпангоута в сечении х, а сила инерции окружающей отсек воды -

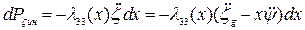, (4.3)

где - присоединенная масса плоского шпангоута.

Кроме сил гидромеханической природы на отсек будут действовать сила веса 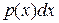и сила инерции массы отсека .

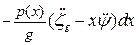Сумма всех сил, действующих на элементарный отсек, будет равна

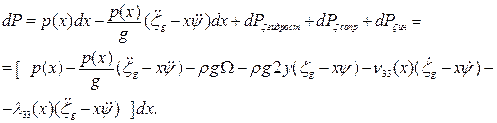(4.4)

Выражение в квадратных скобках дает интенсивность поперечной нагрузки на единицу длины корабля. Статический момент относительно оси Gy всех сил, действующих на отсек, можно записать в виде:

(4.5)

Кроме приведенных в этих выражениях сил на элементарный отсек дей-ствуют еще внутренние силы, создаваемые воздействием на него соседних элементарных отсеков, однако при интегрировании эти силы взаимно уничто-жаются.

Для корабля в целом сумма всех сил и моментов должна быть равна 0, т.е.

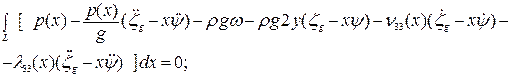(4.6)

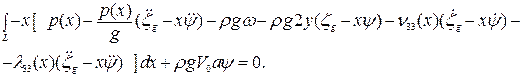(4.7)

В уравнении (4.7) добавлен момент 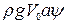, возникающий из-за того, что ЦТ и центр величины (ЦВ) корабля расположены на разной высоте. Величина а - это превышение ЦТ над ЦВ.

Выпишем значения ряда интегралов в готовом виде, предполагая, что при чтении лекций преподаватель остановится на их выводах более подробно:

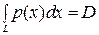- вес корабля (весовое водоизмещение);

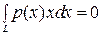- статический момент сил веса, равный 0, так как начало координат находится в ЦТ корабля;

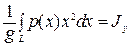- момент сил инерции массы корпуса корабля;

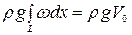- сила поддержания по равновесную ватерлинию;

- статический момент сил поддержания, равный 0 потому, что ;

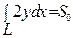- площадь ватерлинии;

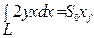- статический момент площади ватерлинии относительно оси Gy;

- абсцисса ЦТ площади ватерлинии;

- момент инерции площади ватерлинии относительно оси Gy;

- коэффициент сопротивления вертикальной качке корабля;

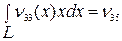- статический момент сил сопротивления качке корабля относительно оси Gy;

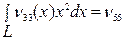- коэффициент сопротивления килевой качке корабля;

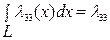- присоединенная масса;

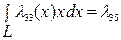- статический момент присоединенной массы корабля отно-сительно оси Gy;

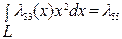- момент инерции присоединенной массы корабля отно-сительно оси Gy.

Подставим значения интегралов в исходные выражения. Тогда получим

;

.

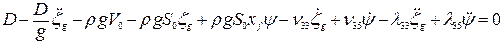После приведения подобных членов и смены знаков окончательно получим

- (4.8)

соответственно уравнения вертикальной и продольной качки корабля на тихой воде без хода.

При написании (4.8) и (4.9) учтено, что и

,

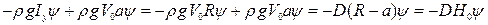где – продольный метацентрический радиус; - продольная мета-центрическая высота. В соответствии с рис. 4.2 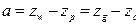, где 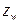- аппликата ЦВ корабля в координатах качки; - аппликата ЦТ в координатах качки; - аппликата ЦВ в координатах статики; - аппликата ЦТ в координатах статики.

Уравнения (4.8) разделяются при малых колебаниях и тогда получаются ранее описанные нами в п. 3.4 отдельные уравнения вертикальной и килевой качки на тихой воде.

Рис. 4.2. Определение величины а в разных системах координат

Дата добавления: 2015-07-02