Спектральный метод

Статистический метод не дает всех необходимых данных для описания волнения как непрерывного случайного процесса. Более удобен для этих целей спектральный метод, который основан на представлении реального волнения в виде суммы бесконечного числа единичных волн со случайными амплитудами, частотами и фазами, т.е.

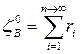cos (k_ix_i - w_it + d_i). (2.26)

Энергия каждой отдельно взятой волны равна

Е_i = 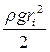. (2.27)

В то же время ее можно представить в виде:

Е_i = s(w_i)Dw_i , (2.28)

где s(w_i) - удельная энергия, приходящаяся на интервал Dw_i, при частоте w_i.

Приравнивая (2.27) и (2.28), получим

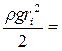s(w_i)Dw_i. (2.29)

Отсюда

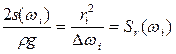. (2.30)

Зависимость S_r(w) (рис. 2.3) называется графиком спектральной плотности или энергетическим спектром. Она характеризует распределение энергии волн по амплитудам и частотам.

Связь между спектральными и статистическими характеристиками можно найти из выражения (2.21), подставив в него (2.29),

D_r = 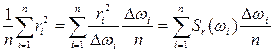. (2.31)

При n ® 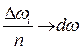, а сумма становится интегралом.

Тогда получим

D_r = 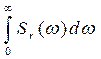. (2.32)

С помощью дисперсии уже легко установить связь с высотой волны заданной обеспеченности и с соответствующими баллами волнения.

Спектры чаще всего представляются в форме

S_r (w) = A w^-ke^-В , (2.33)

где А, В, k, n - параметры, зависящие от условий волнообразования, от степени развитости волнения, от балльности, от акватории и т.д.

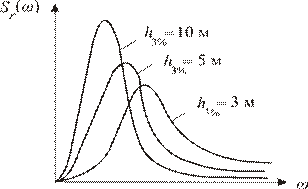
Рис. 2.3. Спектры нерегулярного вол-

нения различной балльности

Обычно спектры нормируют (обезразмеривают), разделив S_r (w) на D_r и умножив на w_ср, т.е. рассматривают

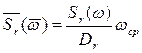, (2.34)

где 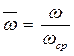- безразмерная частота;

w_ср = 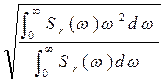. (2.35) Приближенно w_ср можно определить графически (рис.2.4), при этом

w_ср = ,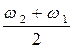

где w ₂ и w ₁ определяются как границы прямоугольника, у которого площадь равна площади под кривой спектральной плотности, а момент инерции площади относительно оси ординат равен моменту инерции площади под кривой.

Дисперсия при нормировании определяется по формуле (2.24).

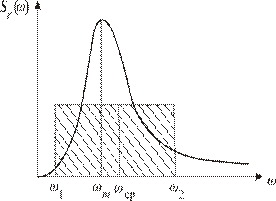
Рис. 2.4. Определение средней частоты спектра

Существует статистическая связь между w_ср и h_3%. Для наиболее употре-бительных спектров

w_ср = 1,74(h_{3 %})^-0,4. (2.36)

Окончательно в нормированном виде спектральная плотность записывается как

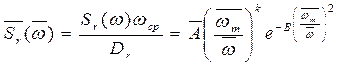, (2.37)

где ;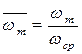

w_m - частота, соответствующая максимуму спектра (рис. 2.4);

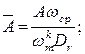
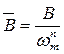. (2.38)

Величина w_m связана с w_ср соотношением, зависящим от вида конкретного спектра.

Перечислим некоторые основные спектры:

- спектр Неймана:

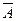= 33,2; k = 6; 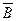= 3; n =2; w_m = 0,707 w_ср;

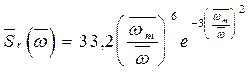; (2.39)

- спектр Бретшнайдера

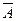= 7,14; k = 5; 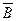= 1,25; n =4; w_m = 0,712 w_ср;

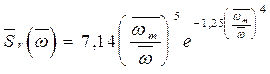;(2.40)

- спектр Вознесенского - Нецветаева (ОСТ по качке)

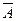= 9,43; k = 6; 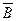= 1,5; n =4; w_m = 0,777 w_ср;

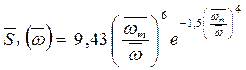. (2.41)

Удобство нормированных спектров в том, что они не зависят от балльности волнения.

Дата добавления: 2015-07-02