О циклических кодах и корнях порождающего полинома с точки зрения конечных полей

Следует отметить, что в данном разделе будет рассмотрено описание циклических кодов с точки зрения конечных полей только в рамках нахождения порождающего полинома. Наиболее понятное полное рассмотрение циклических кодов с точки зрения конечных полей можно найти в книге [2].

Теорема 3. Циклический код длины n с порождающим полиномом g(x) существует тогда и только тогда, когда g(x) делит .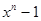

Следствие из теоремы 3. Порождающий полином циклического кода длины n можно найти, разложив полином 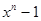на простые множители:

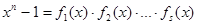
где s – число простых множителей. Произведение произвольного подмножества этих множителей дает порождающей многочлен g(x). Если g(x) – порождающий полином, то он делит 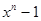, и, следовательно, . Полином g(x) можно найти, найдя все его простые делители.

Простые делители есть не что иное, как функции минимума или минимальные полиномы. Таким образом, зная корни минимальных полиномов, можно легко найти порождающий полином кода. Исходя из сказанного в предыдущих разделах, можно сделать вывод, что поле как раз содержит корни минимальных полиномов, а следовательно содержит корни порождающего полинома.

Резюме:

1. Порождающий полином не что иное, как произведение его простых делителей .

2. Пусть 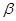- корень полинома 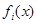. Тогда 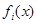не что иное, как функция минимума для .

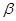3. Имея корни полиномов – делителей g(x) можно найти их функции минимума, и следовательно найти g(x).

4. содержит корни g(x).

Таким образом, нахождение порождающего полинома по степеням его корней сводится к нахождению минимальных полиномов для элементов поля с соответствующей степенью.

,

где 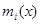минимальный полином.

Дата добавления: 2015-07-02