Пример 7. 12

ПРИМЕР 7.11.

ПРИМЕР 7.10.

ПРИМЕР 7.9.

Пусть в долг на полтора года дана сумма 2000 долл. с условием возврата 3000 долл. Вычислить годовую процентную ставку.

Решение. = НОРМА(1.5,, 2000, -3000). Результат: 31%.

Выдан кредит 200 000 долл. на два с половиной года. Проценты начисляются раз в полгода. Определить величину процентной ставки за период, если известно, что возврат составит 260 000 долл.

Решение. = НОРМА(2.5*2., 200000, -260000). Результат: 5.39%.

Но так как в договорах часто указывается именно годовая ставка, даже если период меньше года, то полученный результат следует обработать функцией

НОМИНАЛ(фактическая ставка, количество периодов в году).

По заданной ставке для периода эта функция возвращает эквивалентную годовую ставку.

В условиях предыдущего примера найти годовую ставку.

Решение. =НОМИНАЛ(5.39%, 2) (год составляют два полугодия). Результат: 5.32%.

С функцией НОМИНАЛ тесно связана функция

ЭФФЕКТ(номинальная ставка, количество периодов в году).

По заданной годовой ставке эта функция возвращает ставку для периода.

Чтобы лучше уяснить понятия номинальной и эффективной ставок, рассмотрим следующий любопытный пример.

Чему равна эффективная ставка: при номинальной ставке 100% и начислении 10 000 000 раз в год, при ежедневном начислении?

Решение. =ЭФФЕКТ(1, 10000000) (=1.71828169);

=ЭФФЕКТ(1.365) (-1.71456748).

Как видим, ответы получились очень близки. А чему равен коэффициент наращения?

= Б3(1/365, 365,, -1) етрудно догадаться, что

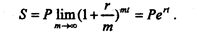
В нашем случае r = 100% = 1

ПРИМЕР 7.13. Определить эффективную ставку сложных процентов, с тем чтобы получить такую же наращенную сумму, как и при использовании номинальной ставки 18% при ежеквартальном начислении процентов.

Наиболее сложной частью анализа постоянной ренты является определение размера выплат. Типичная ситуация здесь такова. Кредитор выдает в начале срока некоторую сумму. Дебитор обязуется погасить задолженность равными долями. При этом каждую выплату можно разбить на две составляющих — одна идет на погашение основной задолженности, а другая — на процентные выплаты.

Для вычисления выплат предназначена функция

Дата добавления: 2015-07-02