ВСД(значения, предположение)

Решение задач средствами Excel по процентной ставке

ОБЩДОХОД(ставка, количество периодов, начальное значение, номер начального периода, номер конечного периода, тип).

Аналогично, функции ПЛПРОЦ соответствует функция ОБЩПЛАТ с теми же аргументами, как и функция ОБЩДОХОД.

ПРИМЕР 7.16. На основе уже созданной таблицы поэкспериментируйте с функциями ОБЩПЛАТ и ОБЩДОХОД. Что получится, если начальный и конечный периоды совпадают, например равны 3? Что получится, если начальный период равен 1, а конечный период равен количеству периодов?

Итак, мы изучили группу финансовых функций для расчета параметров постоянной ренты. Сложность их освоения заклю­чалась в том, что аргументами каждой функции служило не­сколько параметров. Можно выделить пять основных парамет­ров (они перечислены ниже в таблице). Если нам известны че­тыре из этих параметров, то в Ехсеl имеется функция для вычисления пятого, недостающего параметра.

В нижеследующей таблице (рис. 7.8) в левой колонке перечислены пять параметров. В правой колонке для каждого параметра указана функция, с помощью которой можно вычислить этот параметр.

Современное значение (нз)	П3(ставка,кпер,плата,нз,тип)
Будущее значение (бз)	Б3(ставка,кпер,плата,нз,тип)
Плата	ППЛАТ(ставка,кпер,нз,бз,тип) = ОСНПЛАТ + ПЛПРОЦ
Количество периодов (кпер)	КПЕР(ставка, плата, нз, бз,тип).
Ставка	НОРМА(кпер,плата,нз,бз,тип,нач прибл)

Рис. 7.8

Цель работы: Решение задач по общему потоку платежей

Теоретическая часть.

Рассмотрим поток платежей, совершаемых через одинаковые промежутки времени, но сами выплаты могут различаться и по величине, и по знаку. Здесь представляет интерес, задача: даны поток платежей и процентная ставка, вычислить современное значение (present value), т.е. привести все платежи к начальному моменту времени и вычислить эффективную процентную ставку операции. Для этого предназначены две функции ЧПС ( в некоторых версиях Excel вместо ЧПС используется функция НПЗ) — чистое (нетто) приведенное значение (NPV — net present value) и ВСД ( иногда используется функция ВНДОХ) — внутренняя доходность (IRR. — internal rate of return).

Они имеют синтаксис:

ЧПС(ставка, выплаты),

Пусть R₁— выплата в конце первого периода, R₂— выплата в конце второго периода и т.д. Тогда NPV вычисляется по формуле

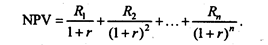
Если имеется выплата в начале первого периода R₀, то она должна добавляться к NPV. Выплаты R_i, могут иметь разные знаки и равняться нулю. Но процентная ставка r и длина периодов неизменны.

Внутренняя доходность вычисляется Ехсеl как решение уравнения

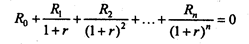
относительно r. Уравнение может иметь несколько решений, поэтому последний аргумент ВСД — начальное приближение. Обратите внимание, что вместо вычисления функции ВСД можно решать уравнение ЧПС(ставка, {R₀, R₁,...,R_n}) относительно ставки. При этом в знаменателе ле­вой части такого уравнения появляется лишний множитель (1+r), но он не оказывает влияния на решение уравнения.

Об их практическом применении можно прочитайте в Справке об этих функциях. Там приведены дополнительная информация и примеры.

Рассмотрим предположения, на которых было основано использование рассмотренных финансовых функций:

• процентная ставка неизменна;

• выплаты происходят равными суммами через одинаковые промежутки времени.

На практике эти предположения часто не выполняются. Поэтому в Ехсеl имеется ряд функций, которые как бы являются обобщением уже рассмотренных функций. Эти функции входят в "Пакет анализа", и с ними можно работать, только если "Пакет анализа" подключен.

Сначала рассмотрим функцию БЗРАСПИС, которая позволяет вычислять будущее значение при плавающей процентной ставке.

Задание 8.1.

Срок ссуды — 5 лет, договорная процентная ставка 12% годовых плюс маржа 0,5% в первые два года и 0,75% — в оставшиеся. Вычислить множитель наращения.

Решение. На рис. 8.1 приведены три варианта решения задачи. Первое решение (в ячейке А1) выполнено на основе функции БС. В ячейке А2 приведено решение, ис­пользующее функцию БЗРАСПИС(современное_значение, массив_ставок).

	A	B
1.	1.8140727	=БС(12.75%,3,0,-БЗ(12.5%,2,0,-1))
2.	1.8140727	=БЗРАСПИС(1,{0.125;0.125;0.1275;0.1275})
3.
4.	12.5% 1&.Э/0	12%+ 0.5%
5.	12.5% 1Л..У/о	12%+ 0.5%
6.	12.75% 1&. (Э /О	12%+ 0.75%
7.	12.75%	12%+ 0.75%
8.	12.75%	12%+ 0.75%
9.	1.8140727	=БЗРАСПИС(1,А4:А8)

Рис. 8.1

Обратите внимание на два момента. Во-первых, современное_значение взято со знаком плюс, и с таким же знаком получен результат. Во-вторых, элементы массива — обычные десятичные дроби, а не проценты. Если в качестве второго аргумента взять массив процентов, это будет воспринято как ошибка.

В ячейке А9 дан третий вариант решения, когда второй аргумент функции БЗРАСПИС — это ссылка на блок, содержащий массив процентных ставок, выраженных в привычном процентном формате.

Дата добавления: 2015-07-02