Операторная функция передачи и ее основные свойства.

Операторной функцией передачи называется отношение операторной реакции цепи к операторному воздействию при нулевых начальных условиях.

Если воздействие и реакция являются напряжениями (рис. 3.8), то операторная функция передачи

(3.24)

Другие возможные варианты:

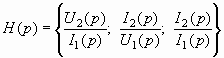
В определении индекс 1 относится к воздействию, а индекс 2 – к реакции. В дальнейшем будем рассматривать (3.24) имея в виду, что полученные результаты будут справедливы и для других вариантов функции передачи. Из определения следует, что передаточная функция связывает реакцию и воздействие:

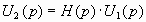
(3.25)

Таким образом, по известной операторной функции может быть определена реакция цепи на заданное воздействие. Причем это может быть сделано в самом общем переходном режиме работы электрической цепи. Поэтому операторная функция передачи содержит полную информацию о цепи, является самой общей функцией цепи и по ней, как будет показано, могут быть определены все другие функции цепи (АЧХ, ФЧХ, переходная, импульсная).

Если рассматривать электрическую цепь с двумя зажимами (двухполюсник), тогда и воздействие и реакция (U₁ (p); I₁ (p)) будут определяться на одной паре зажимов. При этом в качестве операторной функции передачи, как частный случай, рассматривается входная функция: операторное сопротивление или операторная проводимость

В качестве примера рассмотрим определение операторной функции передачи для последовательного RCL – контура, когда реакцией является напряжение на емкости, а воздействием – напряжение на входе цепи (рис. 3.9)

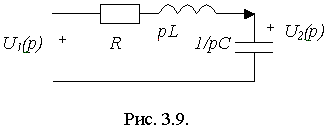
Общий подход к определению функции передачи следующий: считаем, что операторное воздействие U₁ (p) задано и любым известным методом определяем выражение для операторной реакции. При этом получим выражение вида (3.25), из которого легко определить функцию передачи.

Руководствуясь этим подходом, определим:

где p₁ и p₂ корни полинома знаменателя функции передачи.

В данном случае получили функцию передачи с полиномом второго порядка относительно комплексной переменной (оператора) p, в знаменателе. Коэффициенты этого полинома определяются вещественными параметрами цепи.

В общем случае операторная функция передачи является дробно-рациональной (отношение полиномов) функцией с вещественными коэффициентами:

(3.26)

Это утверждение следует из того, что H (p) получается в результате рациональных алгебраических операций с элементами операторной схемы замещения 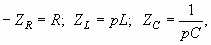которые представляют собой простейшие дробно-рациональные выражения относительно комплексной переменной “ p ”.

Степени полиномов числителя и знаменателя функции передачи зависят от числа реактивных элементов и схемы цепи. Для реальных цепей n ³ m. Если в (3.26) полиномы числителя и знаменателя представить в виде произведения множителей - двучленов, то получим так называемое полюсно – нулевое представление функции передачи

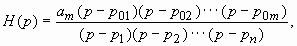
(3.27)

где p_0i (i =1,2… m) - корни полинома числителя, которые называются нулями функции передачи; p_k (k =1,2… n) - корни полинома знаменателя, которые называются полюсами функции передачи. Нуль представляет значение комплексной переменной, при котором функция передачи обращается в нуль, а полюс – значение комплексной переменной, при котором функция передачи обращается в бесконечность. Нули и полюсы функций цепи, имеющих вещественные коэффициенты могут быть вещественными, (p_k=a_k) либо комплексными попарно сопряженными

Рассмотрим взаимосвязь операторной функции передачи и дифференциального уравнения цепи. Для этого перепишем (3.25), используя (3.26), в следующем виде

Согласно свойству об изображении производной преобразования Лапласа при нулевых начальных условиях умножение изображения на p^k соответствует взятию k -той производной от оригинала. Учитывая это и переходя к оригиналам от обеих частей равенства, получим дифференциальное уравнение

(3.28)

Таким образом, функция передачи найденная из операторной схемы замещения, фактически представляет собой символическую запись дифференциального уравнения относительно выбранной переменной. Очевидно, что характеристическое уравнение для дифференциального уравнения (3.28) имеет вид

(3.29)

Таким образом, характеристический полином (3.29) совпадает с полиномом знаменателя функции передачи (3.26). Корни характеристического уравнения совпадают с полюсами операторной функции передачи p_k и определяют свободную (собственную) составляющую реакции:

(3.30)

где A_k – постоянная интегрирования.

Операторные функции передачи устойчивых цепей. Электрическая цепь считается устойчивой, если свободные колебания ограничены u_2св (t) ® 0 при t ®Ґ Свободные колебания определяют переходный процесс и согласно (3.30) зависят от полюсов операторной функции передачи. Для реальных RLC – электрических цепей, полюсы функции передачи можно подразделить на два вида:

1. Вещественные p_k=a_k

2. Комплексные попарно сопряженные

В первом случае соответствующее слагаемое в (3.30)

и для устойчивой цепи должно выполняться условие: a _k < 0, т. к. в противном случае рассматриваемое слагаемое дает неограниченное возрастание колебаний (рис. 3.10)

Во втором случае

где A_k и A_-k комплексные сопряженные числа.

Рассматриваемое слагаемое представляет из себя синусоидальное колебание, амплитуда которого изменяется по экспоненциальному закону с показателем a_k. Если этот показатель будет отрицательным, то колебания будут затухающими (рис. 3.11а), в противном случае – возрастающим (рис. 3.11б).

Таким образом, для устойчивых цепей операторная функция передачи должна иметь полюсы с отрицательными вещественными частями. Для наглядности полюсы изображают на плоскости комплексного переменного p в виде крестиков. На рис. 3.12 изображены полюсы некоторой устойчивой цепи с отрицательными вещественными частями. Как видно полюсы функций передачи устойчивых цепей располагаются в левой полуплоскости комплексного переменного p.

Связь операторной функции передачи с АЧХ и ФЧХ. Как известно, АЧХ и ФЧХ цепи определяются из комплексной функции передачи

где 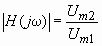- зависимость от частоты отношения амплитуды гармонической реакции U_m2 к амплитуде гармонического воздействия U_m1 (АЧХ); - зависимость от частоты разности начальных фаз реакции и воздействия.

Комплексная схема замещения из которой определяется комплексная функция передачи H (jw), отличается от операторной схемы замещения, из которой определяется операторная функция, тем, что в первой представлены комплексные сопротивления, а во второй – операторные. Таким образом, комплексная передаточная функция формально может рассматриваться как частный случай операторной функции передачи при замене переменной p на комплексную частоту jw, т. е.

(3.31)

Таким образом, АЧХ равна модулю, а ФЧХ – аргументу операторной передаточной функции H (p) при p=jw.

Несмотря на простую связь между операторной и комплексной функциями передачи между ними имеется принципиальные различия.

Первая связывает реакцию и воздействие в наиболее общем случае переходных колебаний, а вторая в частном режиме установившихся гармонических колебаний.

Связь операторной функции передачи с переходной и импульсной характеристиками. Переходная характеристика h (t) численно равна реакции цепи u₂ (t) на воздействие u₁ (t)= 1 (t) единичной ступенчатой функции. Изображение такого воздействия найдем по таблице 3.1 U₁(p)=1/p. Тогда, согласно (3.25), можно найти изображение реакции, т. е. переходной характеристики:

(3.32)

Для того чтобы вычислить переходную характеристику нужно определить операторную функцию передачи, разделить ее на переменную p и от полученного выражения перейти к оригиналу.

Импульсная характеристика численно равна реакции цепи u₂(t) на воздействие u₁(t)=d (t) единичной импульсной функции, которая имеет изображение U₁(p)=1 (см. табл. 3.1).

Используя (3.25) найдем изображение импульсной характеристики

(3.33)

Импульсная характеристика имеет своим изображением операторную функцию передачи.

Часто для вычисления импульсной и переходной характеристик по операторной функции передачи используют формулу разложения (3.23). Предположим, что функция передачи Тогда из (3.33) и (3.32) по формуле разложения получим:

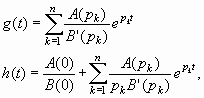
где p_k – полюсы операторной функции передачи.

Дата добавления: 2015-07-02