Передаточное число и передаточное отношение тягового привода

Силы, возникающие при работе тягового привода III класса

Динамика тягового привода II класса с учетом вертикальных перемещений рамы тележки.

Динамика тягового привода II класса без учета вертикального перемещения подрессоренных масс тележки.

Силы, возникающие при работе тягового привода II класса

Динамика привода 1 класса

Силы, возникающие в приводе 1 класса при работе тягового двигателя.

Рассмотрим силы, возникающие в отдельных элементах и узлах привода при движении локомотива с равномерной скоростью по абсолютно ровному пути, при установившемся режиме движения. В этих условиях электромагнитный момент на валу якоря (М_дв = const) и передаточное отношение (µ= ) редуктора остаются постоянными.

На зубцы зубчатого колеса со стороны шестерни будет действовать вертикальная сила Z,направленная вниз. Приведем ее к центру оси колесной пары, приложив здесь две равные и противоположно направленные силы Z.

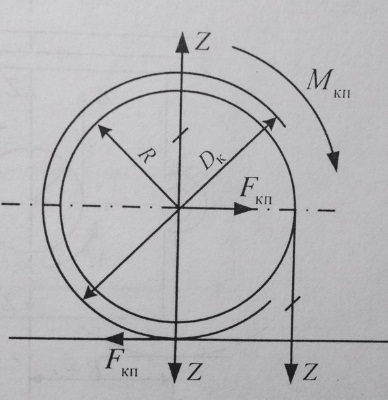
Вращающий момент КП М_кп=Z*R удобно выразить через касательную силу тяги:

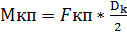, кН*м.

Вертикальная сила Z, приложенная к оси колесной пары в плоскости зубчатого колеса:

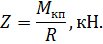
Рассмотрим силы, действующие на корпус тягового двигателя.

Со стороны зубцов зубчатого колеса действует вертикальная реакция, равная по величине силе Z, но направленная вверх.

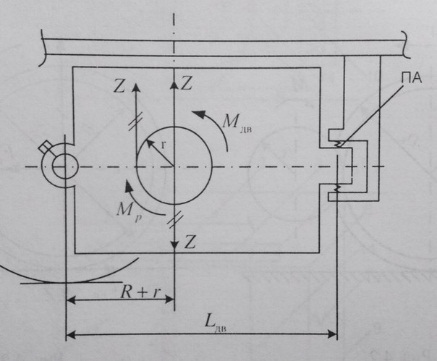
Приведем ее к центру вала якоря, приложив здесь две равные и противоположно направленные силы Z. Получаем пару сил с моментом М_кп=Z*R и вертикальную силу Z, приложенную к валу якоря и передающуюся на корпус двигателя через якорные подшипники. Силу Z можно представить в виде двух составляющих К и Р, соответственно разгружающих колесную пару и подвесной аппарат:

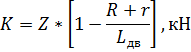
Где 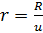– радиус шестерни, м.

Сила К приложена к оси колесной пары в месте установки моторно-осевых подшипников.

Далее находим Р:

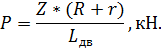
Сила Р приложена к поперечному креплению рамы тележки в месте установки подвесного аппарата.

Вращающий момент 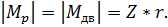Этот момент можно представить в виде пары сил.

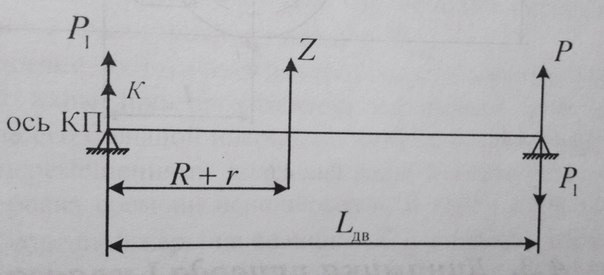
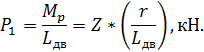
В результате на ось колесной пары действует вертикальная сила:

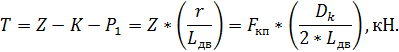
Где 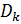– диаметр круга катания движущего колеса. 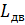- база тягового двигателя. 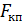- сила тяги, реализуемая одной движущей колесной парой.

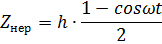
h – глубина неровности.

Угловая частота вертикальных перемещений:

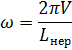
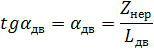
Центр колеса перемещается относительно центра шестерни на величину Z=Zнер-Zдв.

Это ведет к перекатыванию шестерни по зубчатому колесу и повороту якоря на угол: αя=(R+r)*αдв/r=(1+u)*αдв, где u=R/r – передаточное число редуктора.

Полное давление на путь КП: Рполн=Рдин+Рстатич

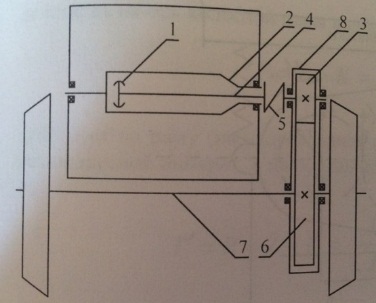
Рассмотрим ТП 2 класса, характеризуемый опорно-рамным подвешиванием ТЭД и опорно-осевым подвешиванием редуктора. Принципиальная схема ТП 2 класса с зубчатой муфтой 1, расположенной внутри полого вала якоря 2. Вращающий момент от якоря к валу малой шестерни 3 тягового редуктора передается посредством торсионного вала 4 и эластичной дисковой резинокордной муфты 5. Зубчатое колесо редуктора 6 жестко закреплено на оси КП 7, корпус редуктора 8 установлен на ось через подшипники качения.

На зубцы зубчатого колеса со стороны шестерни действует вертикальная сила Z, приведем ее к центру оси, приложив здесь равные, но противоположно направленные силы Z. Получаем момент, действ на ось КП: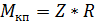

При норм условиях сцепления в точке контакта колеса с рельсом возникает сила тяги, определяемая усл сцепления F_ксц, которая будет приложена к колесу и направлена в сторону движения. Приведя эту силу к оси КП, получаем пару сил с моментом 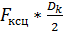, которая будет уравновешивать момент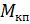

Отсюда следует, что 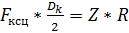и . Такая вертикальная сила будет действовать увеличивая (уменьшая) давление КП на путь в зависимости от направления движения локомотива. Сила, действ на зубцы ЗК, может быть определена в зависимости от скорости движения по тяговой хар-ке и выбранного режима движения.

Приведя силу Z к центру вала шестерни, получим пару сил, уравновешивающую действующий на валу шестерни момент, развив на валу якоря: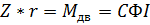

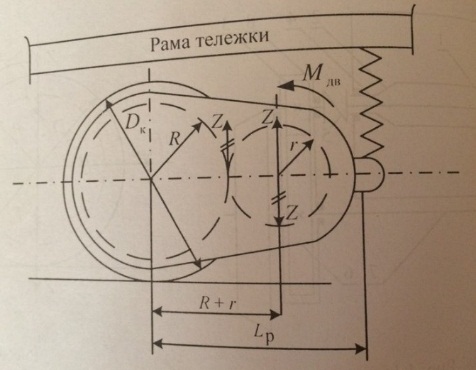
Одновременно на вал шестерни, а от него на редуктор (через подшипники вала шестерни) будет передаваться вертикальная сила Z. Т.к. редуктор опирается на ось и на раму, то сила Z распределяется между осью и КП и подвесным аппаратом

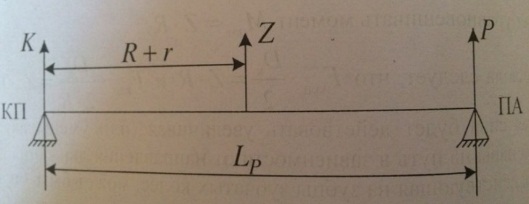
L_p-база редуктора

R+r-централь редуктора

Следовательно, Z=K+P и K*L_p=Z*[L_p-(R+r)]

Из двух этих уравнений видим, что сила:

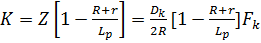- действует на ось колесной пары в направлении вверх, а сила:

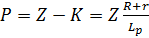(кН)- действует на раму в направлении вверх, через подвесной аппарат, а на ось КП действует вертикальная сила:

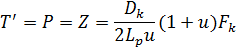
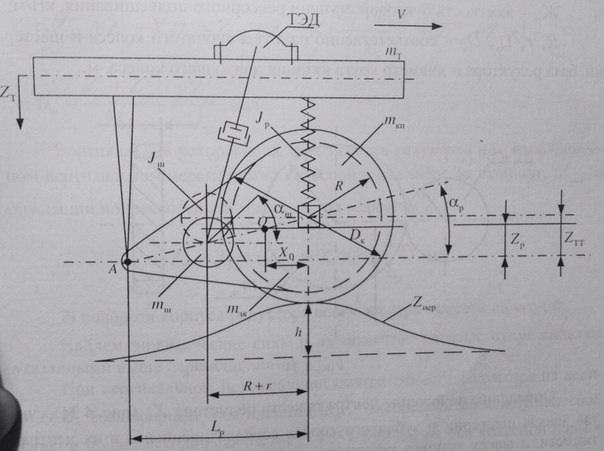
Т.к в приводе II класса присутствует упругая муфта, то нельзя считать, что центр тяжести редуктора совпадает с валом якоря. Расс-м случай, когда редуктор расположен за осью

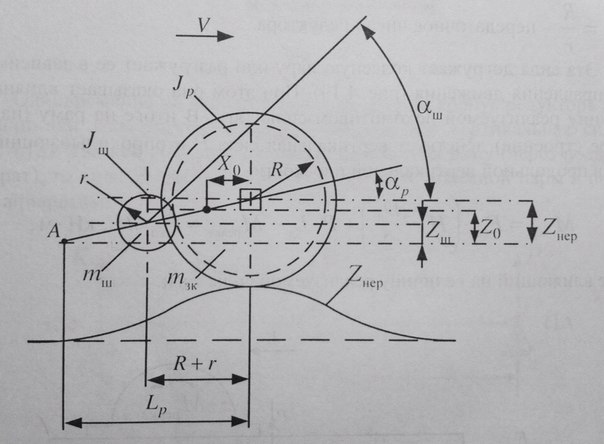
Z_нер - величина неровности.

α _p, α _ш - углы поворота редуктора и вала шестерни, вызванные неровностями.

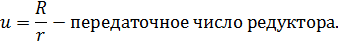
Из схемы следует, что 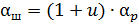, , 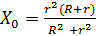- расстояние центра тяжести от оси колесной пары.

Вертикальная координата сила тяжести:

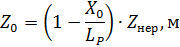
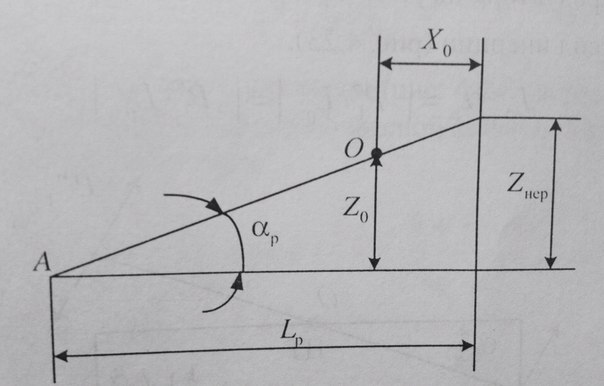
Из рисунка видно, что вертикальные перемещения колесной пары на величину Z_нер можно расс-ть как результат двух движения: верти-го перемещения центра тяжести редуктора и поворота редуктора вокруг центра тяжести на угол α _{p .} Вертикальному перемещению массы редуктора будет противо-ть сила инерции 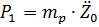. Повороту редуктора на угол α _p препятствует уже пара сил инерции. 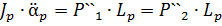, где Р1 – сила, кот догружает КП, Jр – момент инерции редуктора относительно центра тяжести.

Вертикальная сила при этом: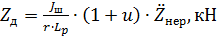

Результирующая вертикальная динамическая нагрузка на ось составит:

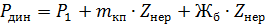(см. рис.)

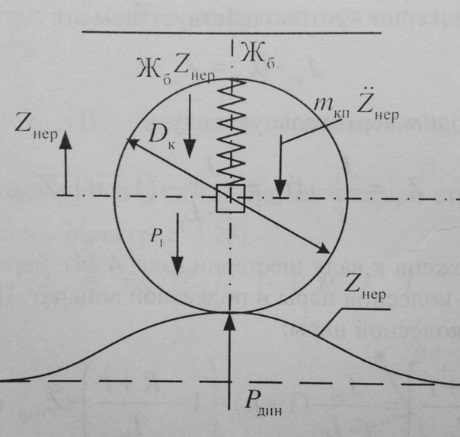
Определим положение центра тяжести редуктора:

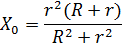
Тогда поворот корпуса редуктора на угол α _p можно представить как результат двух движений:

1) Вертикального перемещения центра его тяжести вверх на величину

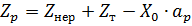гдеZ_т - перемещение центра тяжести.

2) Поворота корпуса редуктора вокруг центра тяжести на угол α _p

При вертикальном перемещении центра тяжести редуктора на величину Z_p, возникающая сила инерции m_pZ_p^.. распределится между колесной парой и подвесным аппаратом, причем на ось колесной пары в плоскости зубчатого колеса будет действовать сила:

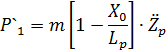
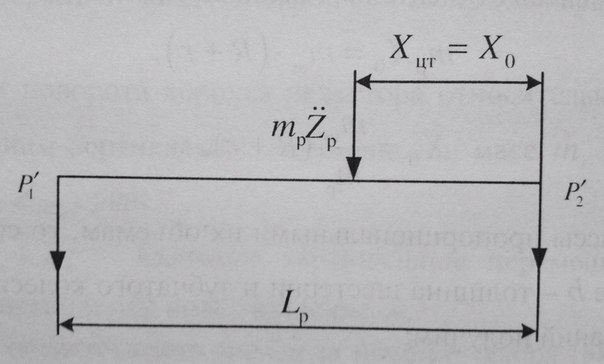
При повороте корпуса редуктора на угол α _p происходит поворот на угол 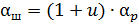под действием вертикальной силы Z_д , возникающий в зацеплении (см. рис.)

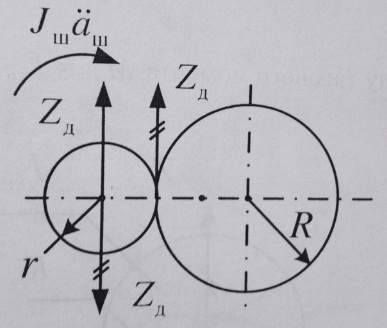
Величина этой силы:

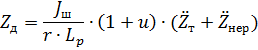
Сила Z_д через зубчатое зацепление действует на зубчатое колесо с динамическим моментом:

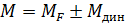
Таким образом можно сделать след-е выводы:

1) Результирующая максимальная вертикальная сила:

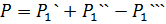
2) На подвесной аппарат действуют результирующая вертикальная сила:

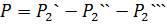
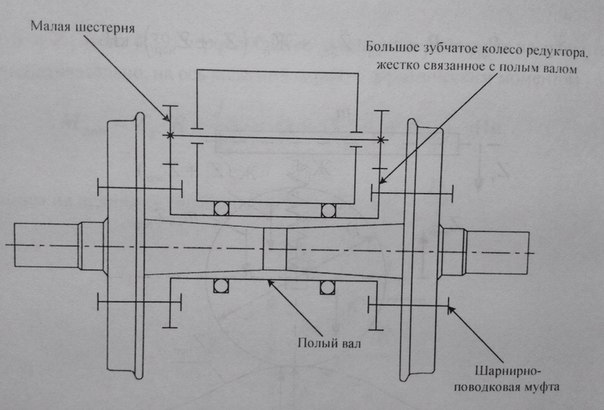
Опорно-рамное подвешивание тягового двигателя и редуктора. Передача момента от вала якоря к КП осуществляется посредством полого вала, охватывающего ось КП и 2ух шарнирно-поводковых муфт. Перемещение рамы тележки относительно оси КП обеспечивается зазором между осью и полым валом.

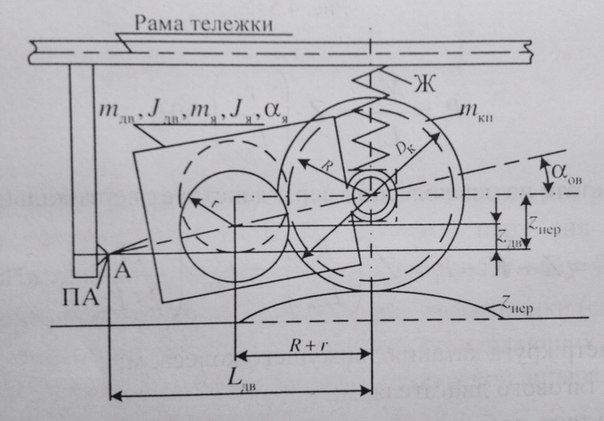
Расчетная схема тяг.привода 3 класса.

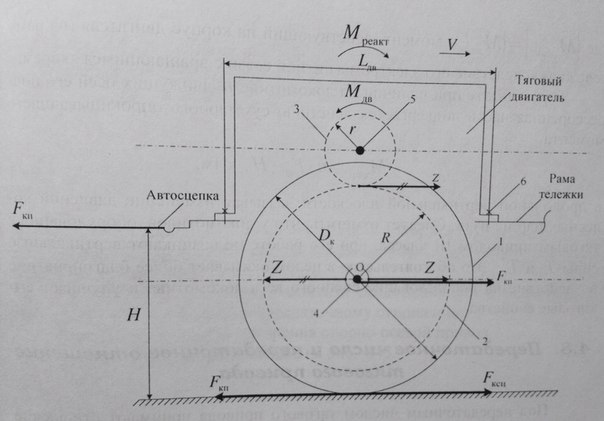
L_дв, D_k,R, r-база двигателя, диаметр круга катания движущего колеса, радиусы зубчатого колеса и шестерни, м

Н- высота оси автосцепки над уровнем головок рельсов, м

О- центр оси КП и зубчатого колеса

1 Движущее колесо 2 Зубчатое колесо, посаженное на вал 3 Шестерня редуктора, посаженная на вал якоря 4 Полый вал, установленный и вращающийся в подшипниках корпуса тяг.двигателя 5 Вал якоря тяг.двигателя 6 Крепление тяг.двиг. к раме тележки

Вращающий момент касательных сил на оси КП.

M_кп=F_кп*D_k/2, где Fкп – касательная сила на ободе движущего колеса

К полому валу приложена сила Z, направленная направо. Нормальное качение колеса по рельсу без проскальзывания: Fкп≤Fксц. Если Fкп>Fксц, возникают условия для боксования. Fкп, приложенная к оси КП, через боксовый узел, раму тележки и автосцепку, передает усилие поезду, обеспечивая его поступательное движение. Надрессорное строение локомотива подвергается действию опрокидывающего момента.

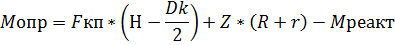
│Мреакт│=│Мдв│- момент, действующий на корпус двигателя из-за его электромагнитной связи с вращ. Якорем. При наличии на локо n движущих осей его подрессоренная часть подвергается- Мопр=n*Fкп*Н, кНм, в продольной вертикальной плоскости, вызывая изм давлений КП на путь.

Передаточное число – отношение диаметра большого зубчатого колеса к диаметру шестерни, на валу якоря ТЭД.

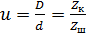
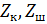-число зубьев большого зубчатого колеса и шестерни

Передаточное отношение-отношение числа оборотов или угловых скоростей вала якоря ТЭД и оси колёсной пары

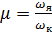
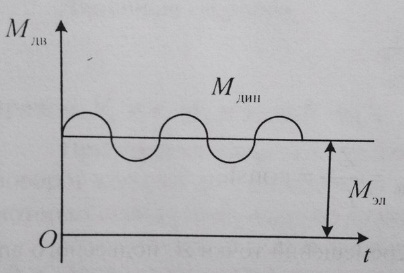
При изменении V, сопровождающейся вертикальными колебаниями подресс массы тележки на валу якоря возникает динамический момент, который созд доп нагрузку на элементы привода и на КП, ухудшая тяговые и динамические хар-ки. Его появление свидетельствует о несовершенстве данного типа привода по передаточному отношению.

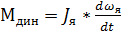
Рассмотрим опорно-осевой привод

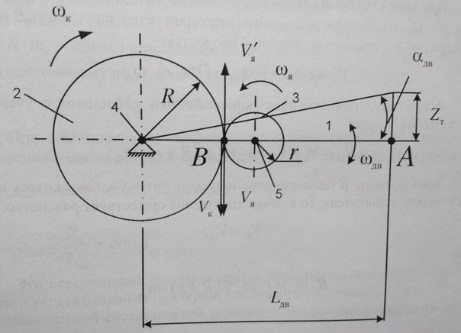
1-корпус ТЭД 2-зубчатое колесо 3-шестерня редуктора 4-ось колёсной пары 5-вал ТЭД А-связь 1 с кронштейном поперечного крепления рамы тележки В-точка зацепления зубчатого колеса и шестерни

Для передаточного отношения тяговой передачи:

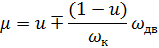
wк wдв – угловые скорости поворота оси КП и корпуса двигателя.

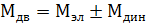
Дата добавления: 2015-07-02