Алгоритм расчета критерия Розенбаума

Задача выявления различий в уровне выраженности исследуемого признака

Для решения задачи выявления различий можно воспользоваться и t-критерием Стьюдента, рассмотренным выше, однако наиболее предпочтительными являются непараметрические критерии Розенбаума (Q) и Манна-Уитни (U).

Примеры гипотез:

H₀: уровни тревожности в группах врачей и психологов достоверно не отличаются.

H₁: уровень тревожности в группе врачей достоверно выше, чем в группе психологов.

1. В каждой из выборок должно быть не менее 11 наблюдений.

Объемы выборок должны примерно совпадать:

· При организации менее 50 наблюдений – разница не более 10;

· От 50 до 100 наблюдений – не больше 20;

· Если организовано более ста наблюдений, то одна из выборок не должна быть больше другой более чем в 1,5 – 2 раза.

2. Упорядочить значения отдельно в каждой выборке по степени возрастания признака.

Считать выборкой 1 ту выборку, значения в которой предположительно выше, а выборкой 2 – ту, где значения предположительно ниже.

3. Определить самое высокое (максимальное) значение в выборке 2.

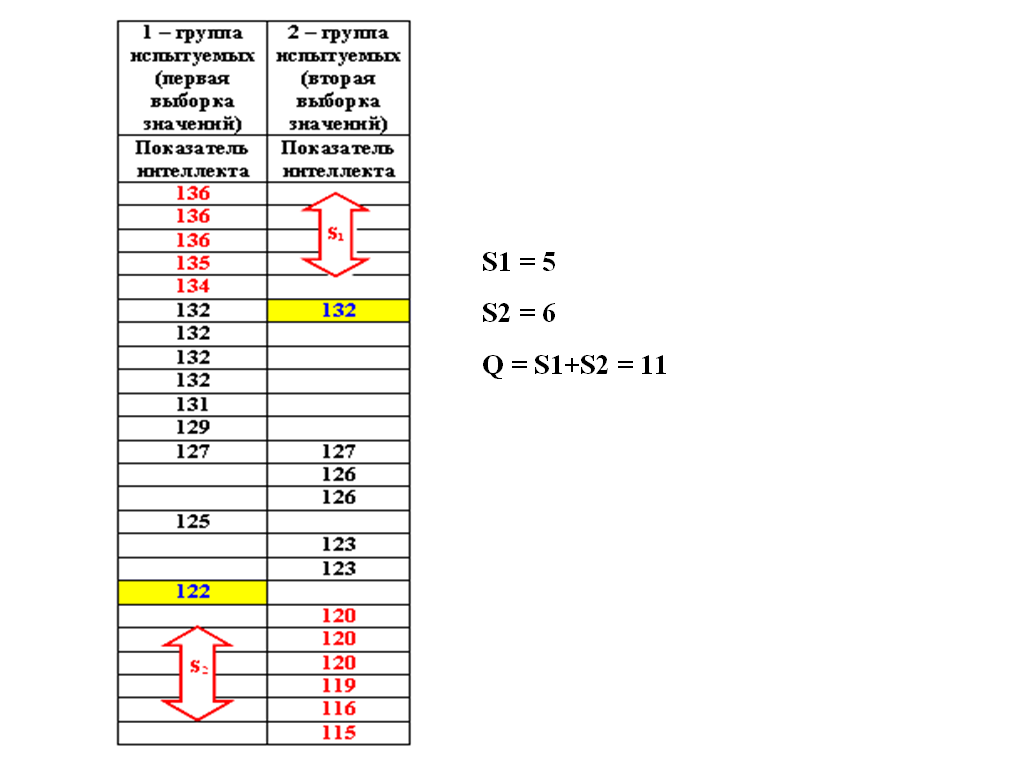
4. Подсчитать количество значений в выборке 1, которые выше максимального значения в выборке 2. Обозначить полученную величину как S1.

5. Определить самое низкое (минимальное) значение в выборке 1.

6. Подсчитать количество значений в выборке 2, которые ниже минимального значения выборки 1. Обозначить полученную величину как S2.

7. Подсчитать эмпирическое значение Q по формуле: Q = S1 + S2.

8. По таблице определить критические значения Q для данных n1 и n2. Если Q_эмп равно Q_0,05 или превышает его, H₀ отвергается.

Пример:

Алгоритм расчета критерия Манна-Уитни

1. Пометить данные испытуемых выборки 1 одним цветом, скажем, красным, а все данные из выборки 2 – другим, например, синим.

2. Расположить все данные в единый ряд по степеням нарастания признака, не считаясь с тем, к какой выборке они относятся, как если бы была одна большая выборка.

3. Проранжировать значения, приписывая меньшему значению меньший ранг.

4. Вновь разделить данные на две группы, ориентируясь на цветные обозначения: красные данные в один ряд, синие – в другой.

5. Подсчитать сумму рангов отдельно по каждой выборке. Проверить, совпадает ли сумма рангов с расчетной.

6. Определить большую из двух ранговых сумм.

7. Определить по формуле значение

,

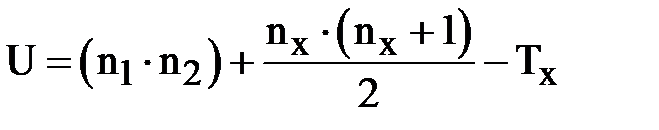где 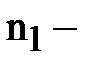количество испытуемых в выборке 1; 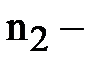количество испытуемых в выборке 2; 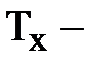большая из двух ранговых сумм; количество испытуемых в группе с большей суммой рангов.

8. Определить критические значения 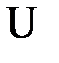. Если 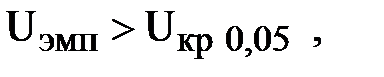то гипотеза 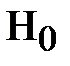принимается. Если 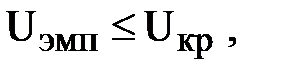то отвергается. Чем меньше значения 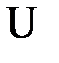, тем достоверность различий выше.

Пример:

Сравнить эффективность двух методов обучения в двух группах. Результаты испытаний представлены в таблице.

1. Перенесем все данные в другую таблицу, выделив данные второй группы подчеркиванием, и делаем ранжирование общей выборки.

Значения		7	8		10	10			14		15	15	16		19	20	29
Ранги	1,5	1,5							9,5	9,5	11,5	11,5
Номер

2. Найдем сумму рангов двух выборок и выберем большую из них: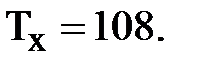

3. Рассчитаем эмпирическое значение критерия по формуле: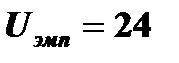

4. Определим критическое значение критерия при уровне значимости p≤0,05 U_0,05=19

Вывод: так как расчетное значение критерия 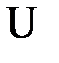больше критического при уровне значимост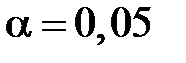и и 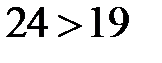, гипотеза о равенстве средних принимается, различия в методиках обучения будут несущественны.

Дата добавления: 2015-07-02