
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Второй замечательный предел
|
|
|
|
.
Если функция имеет предел при, то записывают
.
Или.
Если функция имеет предел справа в точке, то записывают
.
Определение. Число 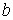 называется пределом функции
называется пределом функции 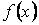 при
при 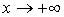 , если для любого положительного числа
, если для любого положительного числа 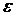 существует положительное число
существует положительное число 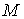 такое, что для всех
такое, что для всех 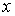 , удовлетворяющих неравенству
, удовлетворяющих неравенству 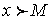 , выполняется неравенство
, выполняется неравенство
Аналогично определяется предел при 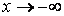 .
.
Определение. Если существуют пределы функции при 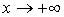 и при
и при 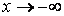 и если эти пределы равны
и если эти пределы равны 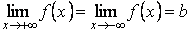 , то говорят, что число
, то говорят, что число 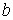 является пределом функции
является пределом функции 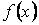 при
при 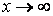 и записывают
и записывают 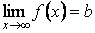
| Признак сходимости последовательности.Если последовательность монотонна и ограничена, то она имеет предел. |
| Этот признак легко иллюстрируется с помощью числовой оси: двигаясь по ней в одну сторону и не имея возможности перейти через поставленный барьер, мы неограниченно приблизимся к некоторой точке числовой оси. |
В примере с корнями 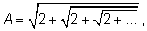 где где 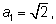 а каждый следующий член последовательности вычисляется по рекуррентной формуле а каждый следующий член последовательности вычисляется по рекуррентной формуле 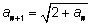 или или 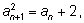 последовательность (an) возрастающая и ограниченная. Действительно, сначала проверим, что an < 2 при всех n.Применим индукцию: последовательность (an) возрастающая и ограниченная. Действительно, сначала проверим, что an < 2 при всех n.Применим индукцию: 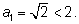 Если an < 2, то an + 2 < 4 и Если an < 2, то an + 2 < 4 и 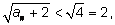 что и утверждалось. Теперь докажем возрастание последовательности. Нам надо доказать, что что и утверждалось. Теперь докажем возрастание последовательности. Нам надо доказать, что  больше, чем an, т. е. проверить неравенство больше, чем an, т. е. проверить неравенство 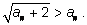 Так как an > 0, то его можно возвести в квадрат и получить для проверки неравенство Так как an > 0, то его можно возвести в квадрат и получить для проверки неравенство 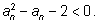 Решая неравенство x2 – x – 2 < 0, получим промежуток (–1; 2), в котором лежат числа последовательности (0 < an < 2). Существование предела полностью доказано. Решая неравенство x2 – x – 2 < 0, получим промежуток (–1; 2), в котором лежат числа последовательности (0 < an < 2). Существование предела полностью доказано.
|
| Принцип сжатой последовательности.Если последовательности (xn) и (zn) сходятся к числу а, а последовательность (yn) такова, что при всех n выполняются неравенства xn ≤ yn ≤ zn то последовательность (yn) сходится к числу а. |
В теории математического анализа доказано, что:
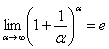
Данный факт носит название второго замечательного предела.
Справка: 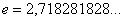 – это иррациональное число.
– это иррациональное число.
В качестве параметра 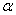 может выступать не только переменная
может выступать не только переменная 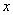 , но и сложная функция. Важно лишь, чтобы она стремилась к бесконечности.
, но и сложная функция. Важно лишь, чтобы она стремилась к бесконечности.
Пример 6
Найти предел 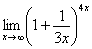
Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.
Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение 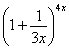 , по какому принципу это делается, разобрано на уроке Пределы. Примеры решений.
, по какому принципу это делается, разобрано на уроке Пределы. Примеры решений.
Нетрудно заметить, что при 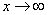 основание степени
основание степени 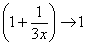 , а показатель –
, а показатель – 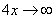 , то есть имеется, неопределенность вида
, то есть имеется, неопределенность вида  :
:
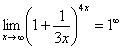
Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр 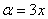 , значит, в показателе нам тоже нужно организовать
, значит, в показателе нам тоже нужно организовать 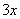 . Для этого возводим основание в степень
. Для этого возводим основание в степень 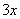 , и, чтобы выражение не изменилось – возводим в степень
, и, чтобы выражение не изменилось – возводим в степень 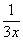 :
:
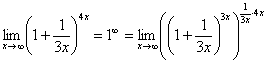
Когда задание оформляется от руки, карандашом помечаем:
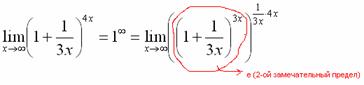
Практически всё готово, страшная степень превратилась в симпатичную букву 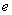 :
:
При этом сам значок предела перемещаем в показатель:
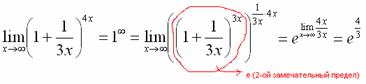
Далее, отметки карандашом я не делаю, принцип оформления, думаю, понятен.
Пример 7
Найти предел 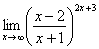
Внимание! Предел подобного типа встречается очень часто, пожалуйста, очень внимательно изучите данный пример.
Пробуем подставить бесконечно большое число в выражение, стоящее под знаком предела:
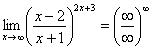
В результате получена неопределенность 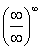 . Но второй замечательный предел применим к неопределенности вида
. Но второй замечательный предел применим к неопределенности вида  . Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас
. Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас 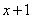 , значит, в числителе тоже нужно организовать
, значит, в числителе тоже нужно организовать 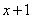 :
:
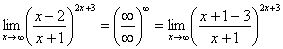
Теперь можно почленно разделить числитель на знаменатель:
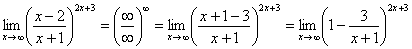
Вроде бы основание стало напоминать 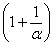 , но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:
, но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:
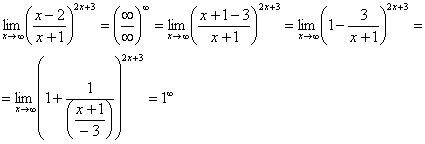
Таким образом, основание приняло вид 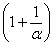 , и, более того, появилась нужная нам неопределенность
, и, более того, появилась нужная нам неопределенность  . Организуем второй замечательный предел
. Организуем второй замечательный предел 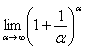 .
.
Легко заметить, что в данном примере 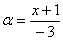 . Снова исполняем наш искусственный прием: возводим основание степени в
. Снова исполняем наш искусственный прием: возводим основание степени в 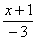 , и, чтобы выражение не изменилось – возводим в обратную дробь
, и, чтобы выражение не изменилось – возводим в обратную дробь 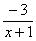 :
:
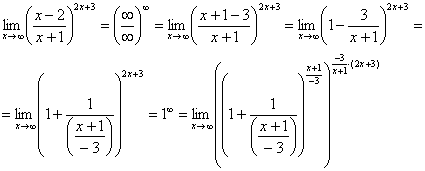
Наконец-то долгожданное 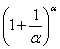 устроено, с чистой совестью превращаем его в букву
устроено, с чистой совестью превращаем его в букву 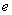 :
:

Но на этом мучения не закончены, в показателе у нас появилась неопределенность вида 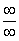 , раскрывать такую неопределенность мы научились на уроке Пределы. Примеры решений. Делим числитель и знаменатель на
, раскрывать такую неопределенность мы научились на уроке Пределы. Примеры решений. Делим числитель и знаменатель на 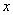 :
:

Готово.
А сейчас мы рассмотрим модификацию второго замечательного предела. Напомню, что второй замечательный предел выглядит следующим образом: 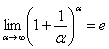 . Однако на практике время от времени можно встретить его «перевёртыш», который в общем виде записывается так:
. Однако на практике время от времени можно встретить его «перевёртыш», который в общем виде записывается так:
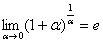
Пример 8
Найти предел 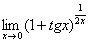
Сначала (мысленно или на черновике) пробуем подставить ноль (бесконечно малое число) в выражение, стоящее под знаком предела:
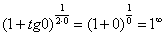
В результате получена знакомая неопределенность  . Очевидно, что в данном примере
. Очевидно, что в данном примере 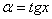 . С помощью знакомого искусственного приема организуем в показателе степени конструкцию
. С помощью знакомого искусственного приема организуем в показателе степени конструкцию 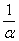 :
:
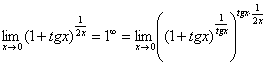
Выражение 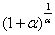 со спокойной душой превращаем в букву
со спокойной душой превращаем в букву 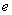 :
:
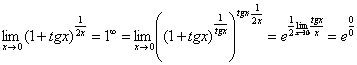
Еще не всё, в показателе у нас появилась неопределенность вида 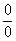 . Раскладываем тангенс на синус и косинус (ничего не напоминает?):
. Раскладываем тангенс на синус и косинус (ничего не напоминает?):
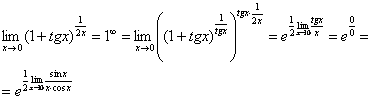
Косинус нуля стремится к единице (не забываем помечать карандашом), поэтому он просто пропадает в произведении:

А что такое 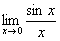 и к чему оно стремится, нужно уже знать, иначе «двойка»!
и к чему оно стремится, нужно уже знать, иначе «двойка»!
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 1773; Нарушение авторских прав?; Мы поможем в написании вашей работы!