
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема об арифмитическом свойстве пределов
|
|
|
|
Если lim (x->a) f(x)=A (+/- oo); lim (x->a) g(x)=B (+/- oo); то
1) lim (x->a) (f(x) +/- g(x)) = A+/- B
2) lim (x->a) f(x)*g(x) = A*B
3) lim (x->a) f(x)/g(x)=A/B (B<>0 g(x)<>0)
Достаточные условия существования конечного предела функции. Теорема (об арифметике). Если для и существуют конечные пределы, то для их суммы и произведения также существуют конечные пределы, причем:;. Если, то существует конечный предел частного:. Док-во. Докажем, например, второе равенство. Пусть существуют конечные пределы и. Докажем, что существует конечный предел. Итак, мы должны доказать, что:. Возьмем произвольное. Найдем из условия, т.е. для этого:. Найдем из условия, т.е. для этого:. Т.к. для по условию существует конечный предел в т., то эта функция будет ограниченной в некоторой окрестности т. (по теореме о локальной ограниченности), т.е. - некоторой константы. Положим. Проверим, что это - искомое. Действительно, В силу произвольности можно считать утверждение доказанным (или можно было искать не по, а по). ▲
5) Теорема о сжатой переменной
Формулировка: Если существуют 3 последовательности, элементы одной из которых начиная с некоторого номера будут между элементами двух других при равных номерах, а также 2 другие последовательности имеют конечные пределы, и эти пределы равны, то наша последовательность тоже будет сходится к конечному пределу,и этот предел будет равен пределам двух других последовательностей.
Доказательство:
аn<bn<cn начиная с некоторого N
предел аn равен d и предел cn равен d
(!) что у последовательности bn тоже есть предел и он равен d
рассмотрим E>0
предел аn равен d, следовательно существует номер N1, начиная с которого |аn-d|<E, то есть E-d<аn<E+d
предел cn равен d, следовательно существует номер N2, начиная с которого |аn-d|<E, то есть E-d<cn<E+d
выберем наибольший из номеров (N)
тогда:
E-d<аn<bn<cn<E+d
то есть E-d<bn<E+d, следовательно последовательность bn имеет конечный предел и он равен d (если последнее не понятно из предыдущей записи, то просто смотрим на теорему №4: предел bn не меньше и не больше d, следовательно равен)
что и требовалась доказать.
2.теорема о сжатой переменной. n>N1 Xn³Zn³Yn $ limXn = lim Yn = a (n®¥) => $ lim Zn=a (n®¥)
Док-во: 1. из того, что $ lim Xn=a (n®¥) => n>N2 |Xn-a|a-E => lim Zn=a (n®¥)
Функция y=f(x) наз-ся ограниченной в данной обл-ти изменения аргумента Х, если сущ-ет положит число М такое, что для всех значений Х, принадлежащих рассматриваемой обл-ти, будет выполн-ся нер-во |f(x)|£M. Если же такого числа М не сущ-ет, то f(x) наз-ся неограниченной в данной обл-ти.
Бесконечно малая величина.
Величина Xn наз-ся бесконечно малой при n®¥, если lim Xn = 0 (n®¥). "E>0, N0, n>N0, |Xn| " E/2 $N1, n>N1 |Xn|" E/2 $N2, n>N2 |Yn|N0, |Xn±Yn|£|Xn|+|Yn| lim(Xn±Yn)=0 (n®¥). Теорема справедлива для любого конечного числа б.м. слагаемых.
2.Произведение ограниченной величины на б.м. величину есть величина б.м.
Док-во:Xn – огр. величина => $ K, |Xn| £ K,
Yn – б.м. => " E/K $N0 n>N0 |Yn| "E $N0 n>N0 |Xn-a| Xn=a+Yn. Справедливо и обратное: если переменную величину можно представить в виде суммы Xn=a+Yn (Yn – б.м.), то lim Xn=a (n®¥).
Бесконечно большая величина
Xn – бесконечно большая n®¥, если "M>0 $N0, n>N0, |Xn|>M => MN1 |Xn|>M
из Yn – б.б. => "M $ N2, n>N2 |Yn|>M
N0=max(N1, N2) => |Xn*Yn|=|Xn||Yn|>MM=M2>M
Lim XnYn=¥ (n®¥).
2.Обратная величина б.м. есть б.б. Обратная величина б.б. есть б.м. lim Xn=¥ (n®¥) – б.б. Yn=1/Xn – б.м. Из lim Xn=¥ => M=1/E $N0, n>N0 |Xn|>M =>n>N0.
|Yn|=1/|Xn|Yn – б.м. => lim Yn=0 (n®¥).
3.Сумма б.б величины и ограниченной есть б.б. величина.
Первый замечательный предел имеет вид: 
На практике чаще встречаются модификации первого замечательного предела в виде

где, k – коэффициент.
Пояснение:

Следствия первого замечательного предела:
1. 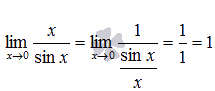
2. 
Эти следствия очень просто доказываются, если использовать правило Лопиталя или заменуэквивалентных бесконечно малых функций.
Разберем несколько примеров нахождения предела по первому замечательному пределу с подробным оприсанием решения.
Пример.
Найти предел не пользуясь правилом Лопиталя 
Решение.
Подставляем значение:
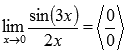
Пришли к неопределенности ноль делить на ноль. Смотрим в таблицу неопределенностей для определения метода решения. Комбинация синуса и его аргумента подсказывает нам о применении первого замечательного предела, но для этого сначала нужно немного преобразовать выражение. Домножим на 3х и числитель и знаменатель дроби.
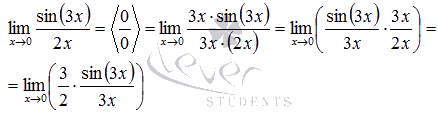
В силу следствия из первого замечательного предела  , поэтому приходим к результату:
, поэтому приходим к результату:

Ответ:

Пример.
Вычислить предел 
Решение.
Подставляем значение:
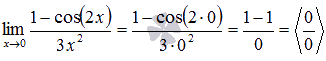
Пришли к неопределенности ноль делить на ноль. Преобразуем числитель, используя формулы тригонометрии.
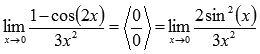
Стало видно, что здесь можно применить первый замечательный предел:

Ответ:
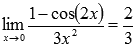
Пример.
Вычислить предел 
Решение.
Подставляем значение:
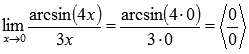
Пришли к неопределенности ноль делить на ноль. Сделаем замену.
Пусть
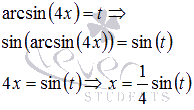
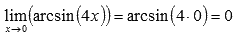 , следовательно,
, следовательно,  при
при  .
.
Тогда предел после замены переменной примет вид:

Ответ:

| Раскрытие неопределенностей |
Неопределенности типа  Пусть заданы две функции f (x) и g (x), такие, что
Пусть заданы две функции f (x) и g (x), такие, что
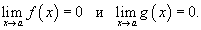 В этом случае говорят, что функция
В этом случае говорят, что функция  имеет неопределенность типа имеет неопределенность типа  в точке x = a. Чтобы найти предел при x = a когда функция в точке x = a. Чтобы найти предел при x = a когда функция  содержит неопределенность содержит неопределенность  , нужно разложить на множители числитель и/или знаменатель и затем сократить члены, стремящиеся к нулю. Примечание: В данном разделе при вычислении пределов не используется правило Лопиталя.
Неопределенности типа , нужно разложить на множители числитель и/или знаменатель и затем сократить члены, стремящиеся к нулю. Примечание: В данном разделе при вычислении пределов не используется правило Лопиталя.
Неопределенности типа  Пусть две функции f (x) и g (x) обладают свойством
Пусть две функции f (x) и g (x) обладают свойством
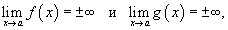 где a является действительным числом, либо стремится к + ∞ или − ∞. Говорят, что в этом случае функция
где a является действительным числом, либо стремится к + ∞ или − ∞. Говорят, что в этом случае функция  имеет в точке a неопределенность типа имеет в точке a неопределенность типа  . Для вычисления предела в этой точке необходимо разделить числитель и знаменатель на x в наивысшей степени.
Неопределенности типа . Для вычисления предела в этой точке необходимо разделить числитель и знаменатель на x в наивысшей степени.
Неопределенности типа  Неопределенности этих типов сводятся к рассмотренным выше неопределенностям типа
Неопределенности этих типов сводятся к рассмотренным выше неопределенностям типа  и и  . .
|
| Пример 1 |
Вычислить предел  .
Решение.
Подставив напрямую значение x = 1, убеждаемся, что данная функция имеет неопределенность .
Решение.
Подставив напрямую значение x = 1, убеждаемся, что данная функция имеет неопределенность  в точке x = 1. Разложив числитель на множители, получаем в точке x = 1. Разложив числитель на множители, получаем
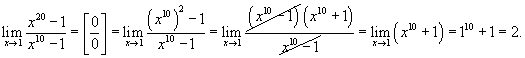
|
| Пример 2 |
Вычислить предел 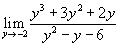 .
Решение.
Функция имеет неопределенность типа .
Решение.
Функция имеет неопределенность типа  в точке y = −2. Разложим числитель и знаменатель на множители. в точке y = −2. Разложим числитель и знаменатель на множители.
 (Мы использовали здесь формулу разложения квадратного трехчлена на множители: ax 2 + bx + c = a (x − x 1)(x − x 2), где x 1 и x 2 - корни квадратного уравнения.) Аналогично,
(Мы использовали здесь формулу разложения квадратного трехчлена на множители: ax 2 + bx + c = a (x − x 1)(x − x 2), где x 1 и x 2 - корни квадратного уравнения.) Аналогично,
 Таким образом, предел равен
Таким образом, предел равен

|
| Пример 3 |
Вычислить предел 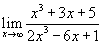 .
Решение.
Подстановка .
Решение.
Подстановка  показывает, что функция имеет неопределенность типа показывает, что функция имеет неопределенность типа  . Разделим числитель и знаменатель на x 3 (x в наивысшей степени знаменателя). В результате получаем . Разделим числитель и знаменатель на x 3 (x в наивысшей степени знаменателя). В результате получаем

|
| Пример 4 |
Вычислить предел 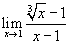 .
Решение.
Перепишем знаменатель в виде .
Решение.
Перепишем знаменатель в виде
 и разложим его как разность кубов:
и разложим его как разность кубов:
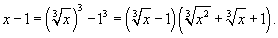 В результате можно найти предел:
В результате можно найти предел:
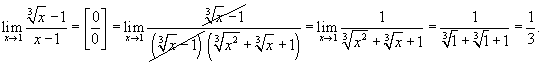
|
| Пример 5 |
Вычислить предел  .
Решение.
Сделаем замену переменной: .
Решение.
Сделаем замену переменной: 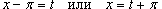 . Тогда . Тогда 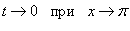 . Получаем . Получаем
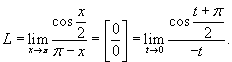 Преобразуем полученное выражение, используя формулу приведения
Преобразуем полученное выражение, используя формулу приведения 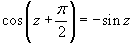 . В результате находим значение предела . В результате находим значение предела

|
| Пример 6 |
Вычислить предел  .
Решение.
Если .
Решение.
Если  , то , то
 Таким образом, здесь мы имеем дело с неопределенностью типа
Таким образом, здесь мы имеем дело с неопределенностью типа  . Умножим и разделим данную иррациональную функцию на сопряженное выражение. . Умножим и разделим данную иррациональную функцию на сопряженное выражение.
 Вычисляя предел каждого члена, получаем ответ:
Вычисляя предел каждого члена, получаем ответ:
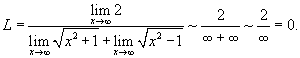
|
| Пример 7 |
Найти предел  .
Решение.
Для вычисления предела избавимся от иррациональностей в числителе и знаменателе, умножив их на соответствующие сопряженные выражения. .
Решение.
Для вычисления предела избавимся от иррациональностей в числителе и знаменателе, умножив их на соответствующие сопряженные выражения.
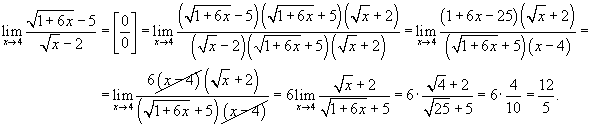
|
| Пример 8 |
Найти предел  .
Решение.
Разделим числитель и знаменатель на x 30 (x в наивысшей степени). Получаем .
Решение.
Разделим числитель и знаменатель на x 30 (x в наивысшей степени). Получаем

|
| Пример 9 |
Найти предел  .
Решение.
Используя формулы .
Решение.
Используя формулы
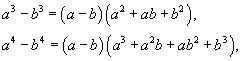 преобразуем предел и найдем его значение:
преобразуем предел и найдем его значение:
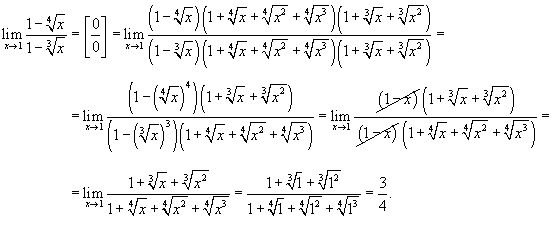
|
| Пример 10 |
Найти предел 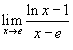 .
Решение.
Пусть .
Решение.
Пусть 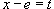 . Тогда . Тогда 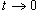 при при  . Следовательно, . Следовательно,
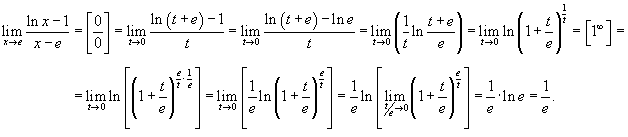
|
| Пример 11 |
Найти предел  .
Решение.
Данная функция определена только при t ≥ 0. Умножим и разделим ее на сопряженное выражение .
Решение.
Данная функция определена только при t ≥ 0. Умножим и разделим ее на сопряженное выражение  . Получаем . Получаем
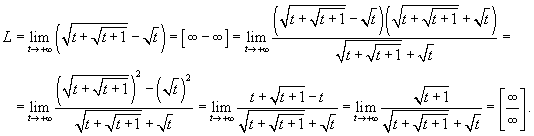 Теперь и числитель, и знаменатель стремятся к ∞ при
Теперь и числитель, и знаменатель стремятся к ∞ при 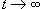 . Следовательно, разделим числитель и знаменатель на . Следовательно, разделим числитель и знаменатель на  - то есть t в наивысшей степени знаменателя. Тогда - то есть t в наивысшей степени знаменателя. Тогда
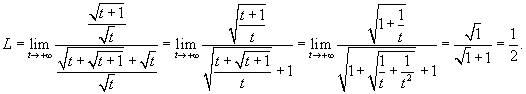
|
| Пример 12 |
Найти предел 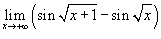 .
Решение.
Используя тригонометричское тождество .
Решение.
Используя тригонометричское тождество 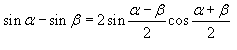 , перепишем предел в следующем виде , перепишем предел в следующем виде
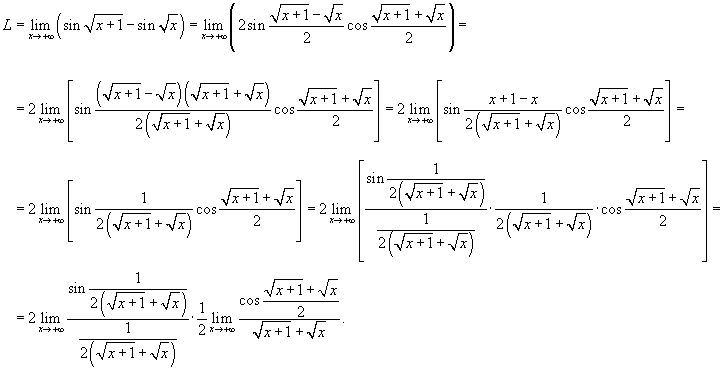 В последнем выражении первый предел, очевидно, равен 1. Во втором пределе функция косинус ограничена в интервале от −1 до 1, а знаменатель стремится к ∞ при
В последнем выражении первый предел, очевидно, равен 1. Во втором пределе функция косинус ограничена в интервале от −1 до 1, а знаменатель стремится к ∞ при  . Поэтому, окончательный ответ равен . Поэтому, окончательный ответ равен

|
Раскрытие неопределённостей вида  ,
, 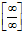
Определение (« на языке последовательностей », или по Гейне)
Число А называется пределом функции y=f (x) в точке х 0 (или при 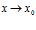 ), если для любой последовательности допустимых значений аргумента xn,
), если для любой последовательности допустимых значений аргумента xn, 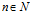 , сходящейся к х 0 (т.е.
, сходящейся к х 0 (т.е.  ), последовательность соответствующих значений функции f (xn),
), последовательность соответствующих значений функции f (xn), 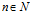 сходится к числу А (т.е.
сходится к числу А (т.е. 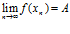 ).
).
Определение (на « языке ε-δ », или по Коши»)
Число А называется пределом функции y=f (x) в точке х 0 (или при 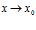 , т.е.
, т.е.  ), если для любого положительно ε найдётся такое положительное число δ, что при всех
), если для любого положительно ε найдётся такое положительное число δ, что при всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 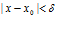 , выполняется неравенство
, выполняется неравенство  .
.
Основные теоремы о пределах
Теорема 1.
Предел суммы (разности) двух функций равен сумме (разности) их пределов:
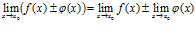
Следствие. Функция может иметь только один предел при 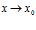 .
.
Теорема 2. Предел произведения двух функций равен произведению их пределов:
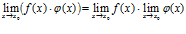
Теоремы 1 и 2 справедливы для любого конечного числа функций.
Следствие. Постоянный множитель можно выносить за знак предела:
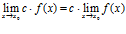
Следствие. Предел степени с натуральным показателем равен той же степени предела:
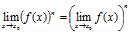
Следствие. 
Теорема. Предел дроби равен пределу числителя, делённому на предел знаменателя, если предел знаменателя не равен нулю:
 , (
, ( )
)
При нахождении пределов применяют соотношения:
 , (k =const);
, (k =const);  ;
;
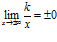 ;
; 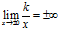 ;
;
 ;
; 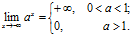
 ;
; 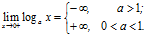
(28).
Постановка задачи. Найти  .
.
План решения. Для того чтобы найти  вычисляем f (х 0), при этом:
вычисляем f (х 0), при этом:
§ если данное выражение имеет смысл, то предел равен этому выражению;
§ если в результате вычислений нет неопределённостей, воспользуемся одним из соотношений (28).
№9. Найти пределы: 1)  ; 2)
; 2)  ;
;
3) 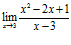 .
.
► 1) Применяя теоремы о пределах, получаем:
 =
= 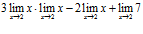 =
=
= 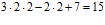 ;
;
2) Пределы числителя и знаменателя существуют и предел знаменателя не равен нулю. Пользуясь теоремой о пределе частного, находим:  =
= 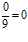 ;
;
3) Непосредственно применять теорему о пределе частного нельзя, так как предел знаменателя равен нулю (в знаменателе есть бесконечно малая величина при  ). В числителе имеем ограниченную величину, отличную от нуля. Таким образом, под знаком предела будет произведение ограниченной величины
). В числителе имеем ограниченную величину, отличную от нуля. Таким образом, под знаком предела будет произведение ограниченной величины  , отличной от нуля, на бесконечно большую величину
, отличной от нуля, на бесконечно большую величину 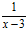 при
при  как величину, обратную бесконечно малой. Поэтому
как величину, обратную бесконечно малой. Поэтому 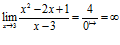 . ◄
. ◄
Постановка задачи. Найти  , где
, где 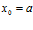 или
или 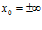 .
.
План решения. Для того чтобы найти  вычисляем f (х 0), если в результате вычислений получилась неопределённость
вычисляем f (х 0), если в результате вычислений получилась неопределённость 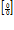 или
или 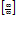 , следует применить соответствующие правила для раскрытия данных неопределённостей.
, следует применить соответствующие правила для раскрытия данных неопределённостей.
Неопределённость вида
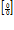
§ Для того чтобы разрешить неопределённость вида 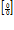 , до вычисления предела средствами алгебры в числителе и знаменателе выделяем множитель
, до вычисления предела средствами алгебры в числителе и знаменателе выделяем множитель  и сокращаем на него, т.к.
и сокращаем на него, т.к.  .
.
§ Чтобы раскрыть неопределённость 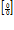 , в которой числитель или знаменатель содержит иррациональность, следует соответствующим образом избавиться от иррациональности.
, в которой числитель или знаменатель содержит иррациональность, следует соответствующим образом избавиться от иррациональности.
Неопределённость вида 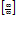
§ Если числитель и знаменатель, сложные степенные функции: необходимо вынести за скобку в числителе и знаменателе дроби неизвестное с наибольшим показателем степени среди всех слагаемых дроби; после сокращения дроби неопределённость устраняется.
Частный случай: предел рационального выражения вида
 при
при 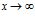 будем рассматривать как предел частного двух многочленов, который равен:
будем рассматривать как предел частного двух многочленов, который равен:
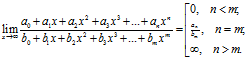
§ Если числитель и знаменатель, сложные показательные функции: за скобку вынести наиболее быстро возрастающее слагаемое среди всех слагаемых дроби; после сокращения дроби неопределённость устраняется.
№10. Найти пределы: 1) 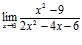 ;2)
;2) 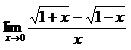 ; 3)
; 3)  .
.
► 1) 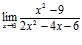 =
= 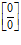 , для раскрытия данной неопределенности средствами алгебры разложим числитель и знаменатель на множители:
, для раскрытия данной неопределенности средствами алгебры разложим числитель и знаменатель на множители:
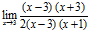 ,
,
сократим множитель (х – 3) имеем:
 =
= 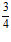 ;
;
2) 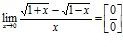 .
.
Данное предельное выражение содержит иррациональность в числителе, следовательно, домножим дробь на сопряженное выражение, т.е. на 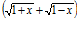 , тогда:
, тогда:
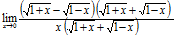 .
.
В числителе последнего выражения получилась формула — разность квадратов, таким образом:
 ;
;
3) 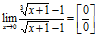 ,
,
для раскрытия данной неопределенности сделаем замену:
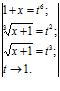
тогда исходное пределное выражение имеетвид:
 ,
,
которое раскрывается по известным правилам, т.е.:
 =
= 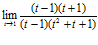 =
= 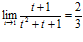 . ◄
. ◄
№11. Найти пределы: 1) 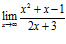 ; 2)
; 2)  ;3)
;3) 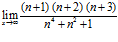 ; 4)
; 4) 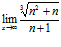 .
.
► 1)  ,
,
для раскрытия данной неопределенности разделим почленно числитель и знаменатель на х 2, тогда:
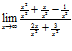 =
=  ;
;
2)  ,
,
для раскрытия данной неопределенности разделим почленно числитель и знаменатель на х 3, тогда:
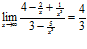 ;
;
3)  ,
,
для раскрытия данной неопределенности разделим почленно числитель и знаменатель на n 4, тогда:
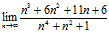 =
= 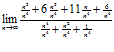 =
=  ;
;
4)  =
= 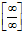 ,
,
для раскрытия данной неопределенности разделим почленно числитель и знаменатель на n, тогда:
 =
=  =0. ◄
=0. ◄
№12. Найти пределы: 1)  ;
;
2) 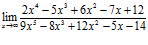 ; 3)
; 3)  .
.
► Данные предельные соотношения можно рссмотреть, как частное двух многочленов, т.е:
1)  =
= 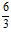 =2;
=2;
2) 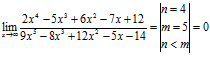 ;
;
3)  .◄
.◄
Постановка задачи. Найти  .
.
План решения. Для того чтобы найти  вычисляем f (х 0), если в результате вычислений получилась одна из неопределённостей
вычисляем f (х 0), если в результате вычислений получилась одна из неопределённостей  ,
,  или др., то данные неопределённости раскрываются путём преобразования и сведения их к неопределённости
или др., то данные неопределённости раскрываются путём преобразования и сведения их к неопределённости 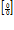 или
или 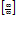 .
.
№13. Найти пределы: 1)  ; 2)
; 2)  .
.
► 1)  ,
,
данное предельное выражение преобразум таким образом:
 =
= 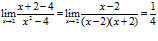 ;
;
2) Рассмотрим два случая:
а) 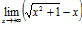 . Перенеся иррациональность из числителя в знаменатель, получим:
. Перенеся иррациональность из числителя в знаменатель, получим:
 =
= 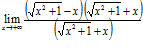 =
= 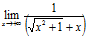 =0;
=0;
б)  .
.
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 1805; Нарушение авторских прав?; Мы поможем в написании вашей работы!