Примеры. Некоторые замечательные пределы

Некоторые замечательные пределы.

Примеры.

1)lim x →1 x 2−4 x 2− x −2=lim x →1(x 2−4)lim x →1(x 2− x −2)=1−41−1−2=32.

2)lim x →2 x 2−4 x 2− x −2

lim x →2(x 2−4)=4−4=0;lim x →2(x 2− x −2)=4−2−2=0.

Таким образом, имеем неопределенность вида 00.

lim x →2 x 2−4 x 2− x −2=[00]=lim x →2(x −2)(x +2)(x −2)(x +1)=lim x →2 x +2 x +1=43.

3)lim x →∞ x 2−4 x 2− x −2=[lim x →∞(x 2−4)=lim x →∞(x 2− x −2)=∞].

Следовательно

lim x →∞ x 2−4 x 2− x −2=[∞∞]=lim x →∞ x 2 x 2−4 x 2 x 2 x 2− xx 2−2 x 2=1.

4)lim x →1 x 2+4 x −5 x 2−1=[00]=lim x →1(x −1)(x +5)(x −1)(x +1)=lim x →1 x +5 x +1=62=3.

5)lim x →∞ x 2+4 x −5 x 2−1=[∞∞]=lim x →∞1−4 x −5 x 21−1 x 2=1.

6)lim x →−1 x 2+4 x −5 x 2−1=1−4−50=∞.

7)lim x →∞(x 3+3 x 2 x 2+1− x)=[∞−∞]=lim x →∞ x 3+3 x 2− x 3− xx 2+1=lim x →∞3 x 2− xx 2+1=lim x →∞3− xx 21+1 x 2=3.

8)lim x →6 x −2−−−−√−2 x −6=[00]=lim x →6(x −2−−−−√−2)(x −2−−−−√+2)(x −6)(x −2−−−−√+2)=

=lim x →6 x −2−4(x −6)(x −2−−−−√+2)=lim x →61 x −2−−−−√+2=14.

9)lim x →∞5 x 6−1 x 12+5 x 5−1−−−−−−−−−−−√=[∞∞]=lim x →∞5−1 x 61+5 x 7−1 x 12−−−−−−−−−−√=5.

10)lim x →∞(x 4+2 x 2−1−−−−−−−−−−√− x 4−2 x 2−1−−−−−−−−−−√)=[∞−∞]=

=lim x →∞(x 4+2 x 2−1−−−−−−−−−−√− x 4−2 x 2−1−−−−−−−−−−√)(x 4+2 x 2−1−−−−−−−−−−√+ x 4−2 x 2−1−−−−−−−−−−√) x 4+2 x 2−1−−−−−−−−−−√+ x 4−2 x 2−1−−−−−−−−−−√=

=lim x →∞ x 4+2 x 2−1− x 4+2 x 2+1 x 4+2 x 2−1−−−−−−−−−−√+ x 4−2 x 2−1−−−−−−−−−−√=

=[∞∞]=lim x →∞4 x 2 x 4+2 x 2−1−−−−−−−−−−√+ x 4−2 x 2−1−−−−−−−−−−√=lim x →∞41+2 x 2−1 x 4−−−−−−−−−√+1−2 x 2−1 x 4−−−−−−−−−√=2.

Вычисление пределов во многих случаях производится с помощью двух
важных формул:

lim x →0sin xx =1;lim x →0(1+ x)1 x = e.

Часто используются следующие формулы, которые являются следствием
вышеприведенных формул.

lim x →∞(1+1 x) x = e.

lim x →0log a (1+ x) x =1ln a, a >0, a ≠1.

Частный случай при a = e:

lim x →0ln(1+ x) x =1.

lim x →0 ax −1 x =ln a, a >0.

В частный случае, когда a = e:

lim x →0 ex −11=1.

Таким образом, можно выписать следующие эквивалентные функции:

sin x ∼ tgx ∼ arctgx ∼ arcsinx ∼ x (x →0);

1−cos x ∼ x 22(x →0);

ex −1∼ln(1+ x)∼ x (x →0);

ax −1∼ x ln a (x →0);

log a (1+ x)∼ x log ae (x →0).

1)lim x →0sin axx =lim x →0 a sin axax = a lim x →0sin axax = a.

Другой способ:

lim x →0sin axx =[sin ax ∼ ax (x →0)]=lim x →0 axx = a.

2)lim x →0 arctgxx =[ y = arctgx; x = tgy ]=lim y →0 ytgy =lim y →0 y sin y cos y =lim y →0cos y sin yy =1.

3)lim x →0 tg 4 x sin x =lim x →0(sin4 x 4 x 4 x cos4 x sin x)=4.

4)lim x →∞(x 2 x +1) x =lim x →∞((2 x 2 x +1)2 x)1212 x =lim x →0⎛⎝(11+12 x)2 x ⎞⎠1212 x =

e −1/2lim x →∞12 x =0.

5)lim x →0 ex 2−cos x sin2 x =lim x →0 ex 2−1+1−cos xx 2=lim x →0 ex 2−1 x 2+lim x →01−cos xx 2=

=[ ex 2−1∼− x 2,(x →0);1−cos x ∼ x 22, x →0]=

=lim x →0− x 2 x 2+lim x →0 x 2/2 x 2=−1+12=12.

6)lim x →0(ln(e + tgαx))1/sin βx =lim x →0(ln(e (1+ tgαxe))1sin βx =

=lim x →0(ln e +ln(1+ tgαxe))1sin βx =lim x →0(1+ln(1+ tgαxe))1sin βx.

При x →0, ln(1+ tgαxe)∼ tgαxe →0. Поэтому

lim x →0(1+ln(1+ tgαxe))1sin βx =

=lim x →0(1+ln(1+ tgαxe))1ln(1+ tgαxe)ln(1+ tgαxe)1sin βx =lim x →0 e ln(1+ tgαxe)sin βx =

= e lim x →0ln(1+ tgαxe)sin βx =[ln(1+ tgαxe)∼ αxe,(x →0);sin βx ∼ βx,(x →0)]=

e lim x →0 αxeβx = eαeβ

7)lim x →0 ctg 2 x (3cos x −3)=lim x →03cos x −3 x 2=lim x →03(3cos x −1−1) x 2=lim x →03(cos x −1)ln3 x 2=

lim x →03ln3(−sin2 x 2) x 2=−6ln3⋅14=−32ln3

Теорема (о локальном повторении функцией свойств предела). Для существования в точке конечного предела необходимо, чтобы в некоторой окрестности этой точки (за исключением самой точки).

Теорема о предельном переходе в неравенствах. Пусть
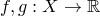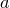, — предельная точка множества 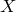, пусть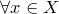 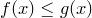. Пусть

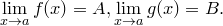
Тогда .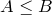

Доказательство. Возьмем , 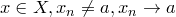. По условию, 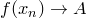, . . 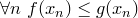Откуда по теореме о предельном переходе в неравенствах для последовательностей вытекает, что .

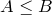Замечание. Из упражнения 2 следует, что в теореме о предельном переходе в неравенствах достаточно предполагать, что неравенство 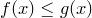справедливо лишь в достаточной близости от точки 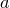, точнее, достаточно предполагать, что найдется такой открытый промежуток 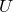, содержащий 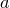, что неравенство 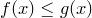выполняется .

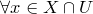Теорема. Пусть 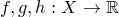, 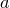— предельная точка множества 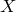. Пусть

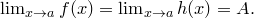
Пусть 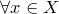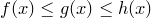. Тогда .

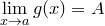Доказательство. Возьмем , .

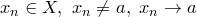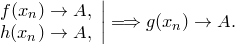
Дата добавления: 2015-07-02