Второй замечательный предел. Первый замечательный предел

Первый замечательный предел

Основные теоремы о пределах

Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов:

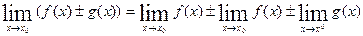
Теорема справедлива для алгебраической суммы любого конечного числа функций.

Теорема 2. Функция может иметь только один предел при .

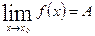
Теорема 3. Предел произведения двух функций равен произведению их пределов:

.

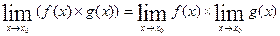Следствие 1. Постоянный множитель можно выносить за знак предела: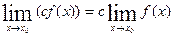

Следствие 2. Предел степени с натуральным показателем равен той же степени предела: .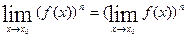

Теорема 4. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю.

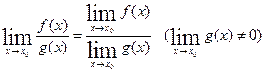
Примеры:

1) = = = =

= = =

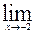
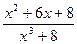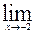
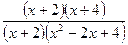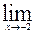
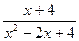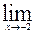
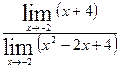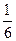
2) =

=

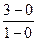
3)

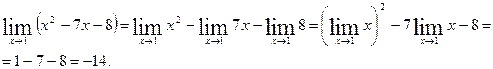
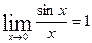
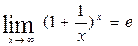или

Постоянное число а называется пределом последовательности {x_n}, если для любого сколь угодно малого положительного числа ε > 0существует номер N, что все значения x_{n ,} у которых n>N, удовлетворяют неравенству

|x_n - a| < ε. (6.1)

Записывают это следующим образом: 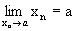или x_n→ a.

Неравенство (6.1) равносильно двойному неравенству

a- ε < x_n < a + ε, (6.2)

которое означает, что точки x _n, начиная с некоторого номера n>N, лежат внутри интервала (a-ε, a+ε), т.е. попадают в какую угодно малую ε-окрестность точки а.

Последовательность, имеющая предел, называется сходящейся, в противном случае - расходящейся.

Понятие предел функции является обобщением понятия предел последовательности, так как предел последовательности можно рассматривать как предел функции x_n = f(n) целочисленного аргумента n.

Пусть дана функция f(x) и пусть a - предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a. Точка a может принадлежать множеству D(f), а может и не принадлежать ему.

Определение 1. Постоянное число А называется предел функции f(x) при x→a, если для всякой последовательности {x_n} значений аргумента, стремящейся к а, соответствующие им последовательности {f(x_n)} имеют один и тот же предел А.

Это определение называют определением предел функции по Гейне, или “ на языке последовательностей ”.

Определение 2. Постоянное число А называется предел функции f(x) при x→a, если, задав произвольное как угодно малое положительное число ε, можно найти такое δ >0 (зависящее от ε), что для всех x, лежащих в ε-окрестности числа а, т.е. для x, удовлетворяющих неравенству
0 < x-a < ε, значения функции f(x) будут лежать в ε-окрестности числа А, т.е. |f(x)-A| < ε.

Это определение называют определением предел функции по Коши, или “на языке ε - δ “.

Определения 1 и 2 равносильны. Если функция f(x) при x → a имеет предел, равный А, это записывается в виде

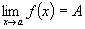. (6.3)

В том случае, если последовательность {f(x_n)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а, то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:

Переменная величина (т.е. последовательность или функция), предел которой равен нулю, называется бесконечно малой величиной.

Переменная величина, предел которой равен бесконечности, называется бесконечно большой величиной.

Чтобы найти предел на практике пользуются следующими теоремами.

Теорема 1. Если существует каждый предел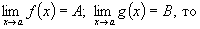

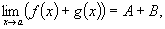(6.4)

(6.5)

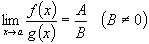(6.6)

Замечание. Выражения вида 0/0, ∞/∞, ∞-∞, 0*∞, - являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и найти предел такого вида носит название “раскрытие неопределенностей”.

Теорема 2. 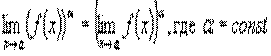(6.7)

т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности, ;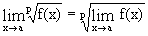

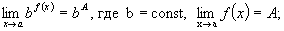(6.8)

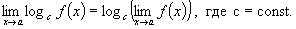(6.9)

Теорема 3.

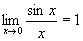(6.10)

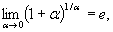(6.11)

где e» 2.7 - основание натурального логарифма. Формулы (6.10) и (6.11) носят название первый замечательного предело и второй замечательный предел.

Используются на практике и следствия формулы (6.11):

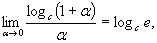(6.12)

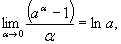(6.13)

(6.14)

в частности предел,

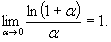
Eсли x→ a и при этом x > a, то пишут x →a + 0. Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x→a и при этом x<a, то пишут x→a-0. Числа 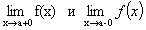и называются соответственно предел справа и предел слева функции f(x) в точке а. Чтобы существовал предел функции f(x) при x→a необходимо и достаточно, чтобы 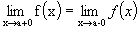. Функция f(x) называется непрерывной в точке x₀, если предел

. (6.15)

Условие (6.15) можно переписать в виде:

,

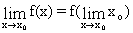то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке.

Если равенство (6.15) нарушено, то говорят, что при x = x_o функция f(x) имеет разрыв. Рассмотрим функцию y = 1/x. Областью определения этой функции является множество R, кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(x_o)= f(0) не определено, поэтому в точке x_o = 0 функция имеет разрыв.

Функция f(x) называется непрерывной справа в точке x_o, если предел

,

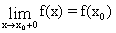и непрерывной слева в точке x_o, если предел

.

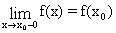Непрерывность функции в точке x_o равносильна ее непрерывности в этой точке одновременно и справа и слева.

Для того, чтобы функция была непрерывна в точке x_o, например, справа, необходимо, во-первых, чтобы существовал конечный предел 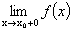, а во-вторых, чтобы этот предел был равен f(x_o). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.

1. Если предел 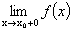существует и не равен f(x_o), то говорят, что функция f(x) в точке x_o имеет разрыв первого рода,или скачок.

2. Если предел 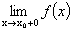равен +∞ или -∞ или не существует, то говорят, что в точке x_o функция имеет разрыв второго рода.

Например, функция y = ctg x при x → +0 имеет предел, равный +∞, значит, в точке x=0 она имеет разрыв второго рода. Функция y = E(x) (целая часть от x) в точках с целыми абсциссами имеет разрывы первого рода, или скачки.

Функция, непрерывная в каждой точке промежутка [a,b], называется непрерывной в [a,b]. Непрерывная функция изображается сплошной кривой.

Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п.

Свойства предела:

1) Если f (x) и g (x) имеют пределы в точке x 0, то функции f (x)± g (x) и f (x) g (x)также имеют пределы в точке x 0, причем

lim x → x 0(f (x)± g (x))=lim x → x 0 f (x)±lim x → x 0 g (x);

lim x → x 0(f (x) g (x))=(lim x → x 0 f (x))(lim x → x 0 g (x))

2) Для любого числа C,lim x → x 0(Cf (x))= C lim x → x 0 f (x)

3) Если функции f (x) и g (x) имеют пределы в точке x 0 и lim x → x 0 g (x)≠0, то функция f (x) g (x) также имеет предел в точке x 0, причем

lim x → x 0 f (x) g (x)=lim x → x 0 f (x)lim x → x 0 g (x).

.

4) Пусть существует lim x → x 0 f (x)= a (f (x)≠ a при x ≠ x 0) и lim y → ag (y); тогда в точке x 0существует предел композиции g (f (x)), причем lim x → x 0 g (f (x))=lim y → ag (y).

Если разность f (x)− g (x) представляет собой неопределенность вида ∞−∞, или частное f (x) g (x) представляет собой при неопрделенность вида ∞∞ или 00, то вычисление пределов называют "раскрытием неопределенностей."

Дата добавления: 2015-07-02