Мажор и минор

Теория гармонии знает важнейшее явление музыки, блестящий период господства которого уже закончился, а исчерпывающего на­учно-теоретического обоснования, с которым были бы согласны все ученые, до сих пор не существует. Это явление — мажор и минор.

Качество, характеризующее специфическую для соотношения мажора и минора противоположную направленность, принято обо­значать как наклонение. Мажор как «твердое» (dur), «большее» (maggiore), минор как «мягкое» (moll), «меньшее» (minore) в их контрастном сопряжении служат мощным средством музыкальной выразительности, средством широкого и многообразного диапазона действия. Мажорность и минорность лежат в основе двух тональных ладов, распространенных в период высшего расцвета европейской музыки начиная с XVIII в. (Бах, Гендель, Гайдн, Моцарт, Бетховен, Шуберт, Шуман, Шопен, Лист, Вагнер, Глинка, Балакирев, Боро­дин, Мусоргский, Чайковский, Римский-Корсаков, Рахманинов, Гла­зунов, Скрябин), ладов, во многом сохраняющих свое значение и для музыки XX в. (Стравинский, Мессиан, особенно Прокофьев, Мясковский, Шостакович, Щедрин и др.). Мажорность и минорность могут играть существенную роль и для экспрессии других ладов, вне мажорно-минорной системы. Например, дорийский и фригийский и некоторые еще — лады минорной основы, миксолидийский, лидий­ский — мажорной основы (открытие Царлино).

Для всех этих противопоставлений основной тип противопо­ложности тот же самый: мажор и минор, dur и moll, «твердое» и «мягкое».

Сами противоположности — «твердое» и «мягкое» — имеют ис­торию много более древнюю, чем мажор и минор как лады или даже как аккорды. Еще в античной Греции встречалось противопоставле­ние «твердой» (или «синтонической», то есть с «острым» натяжени­ем средних струн в тетрахорде) и «мягкой» (со «слабым» натяжени­ем) хромы (у Клавдия Птолемея). А Боэций считал диатон родом «твердым и естественным» (durius et naturalis), хрому — «размяг­ченным» (mollius). Вслед за этим и целый тон (характерный для диатона) противопоставлялся средневековыми теоретиками полуто­ну (характерному для хромы), как интервал «твердый», «совершен­ный», простой — «мягкому», «несовершенному», усложненному. Позднее (в XVI в.) это противопоставление было перенесено и на терции — большую (tertia dura) и малую (tertia mollis; у Й. Коклея).

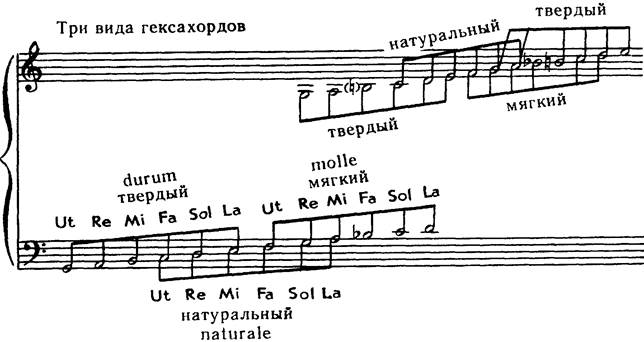
Первыми звукорядами «твердыми» и «мягкими» были истори­чески не наши мажорные и минорные гаммы, а средневековые сольмизационные гексахорды со структурой:

(Их слоги произошли от начальных слогов строк гимна «Ut queant laxis», приспособленного Гвидо Аретинским для практического ос­воения тонов и полутонов звукоряда.)

В системе гексахордов различали три положения гексахорда в зависимости от того, попадает ли в него мягкое b (то есть си-бемоль), или твердое («квадратное») 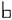(то есть си-бекар), или же не попада­ет ни то ни другое. Соответственно три гексахорда назывались «мяг­ким» (molle), «твердым» (durum) или «натуральным» (naturale) (пример 135).

(Еще Н. П. Дилецкий в 1679-1681 гг. называет музыку в соот­ветствующих звукорядах «дуральной» — без знаков и «бемолярной» — с бемолями.)

В XVII же веке понятия dur и moll стали обозначать ладовое наклонение в зависимости от терции, большой и малой (у Й Кепле­ра genus durum = g-e-d-c-H-G, a genus molle = g-es-d-c-B-G; в конце XVII в., у А. Веркмайстера встречаются обозначения в совре­менном смысле — a-moll, e-moll).

Современная постановка вопроса о мажоре и миноре включает прежде всего три главные проблемы:

1) сущность мажорного и минорного трезвучия;

2) сущность классических мажорного и минорного ладов (тональ­но-функциональной системы);

3) мажорное и минорное наклонения лада в музыке XX в.

Третья из проблем не относится к содержанию настоящей рабо­ты. Вторая решается в основном в главе о тональных функциях. Здесь же пойдет речь о первой проблеме, которая, естественно, свя­зана и с двумя другими.

Первую научную теорию сущности мажора и минора, связи и противоположности двух наклонений предложил знаменитый ита­льянский теоретик музыки Джозеффо Царлино в книге «Основы

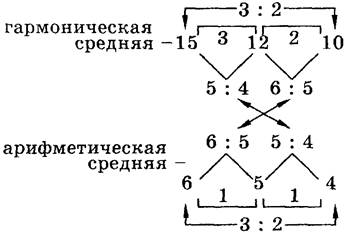
гармонии» (или «Учение о гармонии», букв. «Гармонические на­ставления»; Венеция, 1558). В главе 31 части 3 он дает крайне сжа­то изложенную, но совершенно полно выраженную идею трактовки мажора и минора как эстетических противоположностей на основе древней (еще пифагорейской) эстетической теории пропорций (по изд.: Zarlino G. Le Istitutioni Harmoniche. Venetia, 1573. P. 211). Основные три вида «средних» (арифметическая, гармоническая и геометрическая) или три вида «деления» (те же) Царлино излагает еще в первой части (глава 35 и следующие). Три вида «средних» поясним схемой (ср.: Zarlino G. Le Istitutioni Harmoniche. Venetia, 1573. P. 54; «сверхтретная» пропорция — отношение, когда боль­шее число превышает меньшее на одну треть его):

Таблица 13

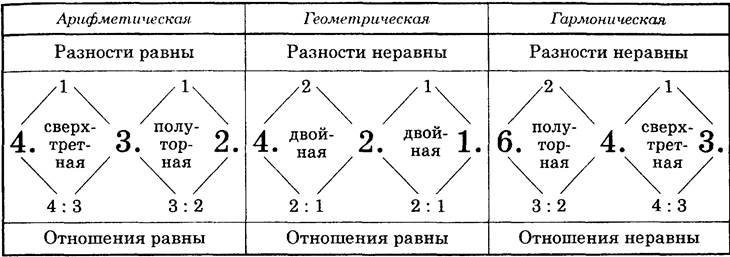
Арифметическая средняя получается при трех числах, где раз­ность первого и второго равна разности второго и третьего. Напри­мер: 4, 3, 2 или 3, 2, 1, или 6, 4, 2, или 7, 4, 1 и т. п.

Геометрическая средняя получается при трех числах, где отноше­ние первого и второго равно отношению второго и третьего. Например: 4, 2, 1 или 9, 3, 1, или 16, 4, 1 и т. п.

Гармоническая средняя получа­ется при трех числах, где отноше­ние разностей первого и второго, вто­рого и третьего равно отношению первого и третьего. Например:

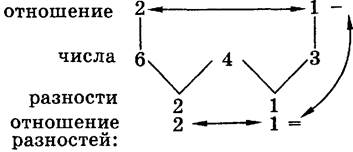
Другие примеры: 6, 3, 2 или 15, 12, 10, или 20, 15, 12, или 28, 7, 4.

Гармоническая средняя — инверсия арифметической:

Арифметическая = 1, ²/₁, ³/₁, ⁴/₁, ⁵/₁, ⁶/₁;

Гармоническая = 1, ^l/₂,¹/₃, ¹/₄, ¹/₅, ¹/₆;

(для пояснения: 1, ¹/₂, ¹/₃ ⁼ 6, 3, 2).

«Все разнообразие и совершенство гармонии» Царлино связыва­ет с действием двух интервалов — квинты и терции или их «репликатов» (то есть производных от них интервалов, например секст). Звуки квинты неизменны, терция же (то есть большая терция) может занимать свое положение внутри квинты, помещаясь либо внизу,

либо вверху, тем самым деля число квинты (3: 2) различным обра­зом. Так как один из звуков терции совпадает либо с нижним, либо с верхним, то к квинте прибавляется еще один звук, соответствую­щий «средней» величине. Отсюда и обоснование мажора и минора теорией «средних». Царлино пишет, что большая терция («la Terza maggiore»), помещаясь в нижней части квинты, делает гармонию «веселой» (allegra), a помещаясь в верхней части — «печальной» (mesta). Имея в виду, что способ обозначения времен Царлино в длинах струн, а не в числах колебаний, мы получаем гармоническую пропорцию как объяснение мажора (мажорного трезвучия) и ариф­метическую — для объяснения минора (если выражать то же самое способом, типичным для нашего времени, — в числах колебаний, то данные будут обратными: гармоническая пропорция — для ми­нора, арифметическая пропорция — для мажора). Та­ким образом, звуки квинты составляют крайние члены:

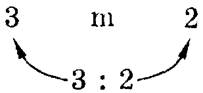
Терция же помещается двояким образом в середине:

В конце главы 31 Царлино делает замечательное заявление: арифмети­ческая пропорциональность немного удаляется от совершенства гармонии, так как ее части не находятся в своем естественном положении; напротив, гармоническая консонирует совершен­но. В этих словах Царлино предчув­ствует ориентацию на «естественный», то есть натуральный порядок звуков (натуральный звукоряд, которого он не знал). По мысли Царлино, мажор и минор равноправны и зако­номерны (так как материализуют в звуках две важнейшие эстетиче­ские закономерности пропорций, которые в принципе равноправны), и вместе с тем мажор близок природе, а минор более от нее удаляет­ся. Отсюда и различие в экспрессии, характере выразительности.

Царлино отметил также, что два эти наклонения — мажор и минор — лежат в основе всех ладов (хотя теоретическая системати­ка ладов у Царлино еще совершенно чужда идее двуладовости систе­мы), и разделил все лады соответственно на две группы:

1) с большой терцией и большой секстой (над финалисом С, F, G);

2) с малой терцией и малой секстой (D, E, А).

Трактовка Николая Дилецкого (1679, 1681) не является глубокой научной теорией, но она очень колоритна по формулировкам и ориги­нальна по обоснованию взаимоотношения мажорного и минорного трезвучий. Формально считая музыку «по смыслу трегубой» (троя­кой, то есть трехладовой) — «веселой, жалостной и смешанной», Дилецкий в действительности базируется на представлении только о двух противоположных ладах, которые он понимает в зависимо­сти от лежащих в их основе трезвучий — ут-ми-соль и ре-фа-ля. Зависимость трактуется однозначно, что свидетельствует о полной осознанности двухладового характера современной Дилецкому си-

стемы: «если будет подавати к пению тон ут, ми, соль, будет веселая мусикия, если тон ре, фа, ля — будет жалостная». Обоснование же того и другого трезвучий Дилецкий получает от Гвидонова гексахор­да (об этом говорят уже сами названия «шести знамений мусикийс­ких» — ут, ре, ми, фа, соль, ля), который совпадает с двумя главны­ми согласиями — «мрачным» и «свет­лым». Гексахорд разделяется «надвое»:

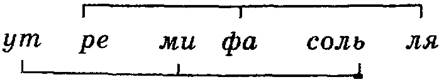
Если Царлино делил различным об­разом квинту, то Дилецкий делит шесть звуков гексахорда, пред­ставляя тем самым своеобразный «модальный» подход.

Немецкий теоретик Мориц Хауптман в книге «Природа гармони­ки и метрики» (1853) для объяснения мажорного и минорного трезву­чий склоняется к так называемой «дуалистической» трактовке, со­гласно которой мажор и минор зеркально противоположны друг дру­гу. Хауптман исходит из того, что существуют только три прямо понимаемых интервала — октава, квинта и (большая) терция. Слива­ясь в монолитное единство, они дают только два аккорда — мажорное и минорное трезвучия. Звуки, от которых строятся эти интервалы и которые тем самым объединяют интервалы в аккорд-монолит, распо­лагаются различно в том и другом аккорде: в мажоре это нижний звук квинты, от которого интервалы направлены вверх (C-G, С-е), в миноре это верхний звук квинты, от которого интервалы направлены вниз. Поэтому звук, объединяющий мажорное созвучие (Klang), име­ет у себя свои квинту и терцию, а звук, объединяющий минорное созвучие, имеется (есть) у своих квинты и терции. Отсюда логиче­ская противоположность между состояниями: действительным (ак­тивным) «иметь» (das Haben) и страдательным (пассивным) «быть» (das Sein). В результате мажорное трезвучие — стремящаяся (вверх) сила,а минорное — опускающаяся (вниз) тяжесть.

Хуго Риман (вместе с другими немецкими теоретиками — А. Эттингеном, Г. Гельмгольцем, 3. Карг-Элертом) развил далее теорию ду­ализма мажора и минора, согласно которой минор понимается как зеркальное отражение (инверсия) мажора. Риман пытался найти для мажора и минора природное, объективное обоснование. Для мажора (мажорного трезвучия) — это, естественно, натуральный звукоряд. Для минора же такового природного обоснования очевидным образом не находится. Риман обратился к теории унтертонов, ряд которых зер­кально симметричен ряду обертонов, отличаясь от него лишь направ­ленностью следования тех же самых интервалов (чисел), пример 136.

Можно найти некоторое подтверждение унтертоновой теории. Так как натуральный ряд (каким является ряд обертоновый и кото­рым Риман хочет представить еще и унтертоны) реализуется в явле­ниях резонанса, то в духе теории Хауптмана начальный тон оберто­нового ряда имеет все прочие, а начальный тон унтертонового име­ется у всех прочих (пример 137).

Однако такое подтверждение не может опровергнуть основного возражения против теории унтертонов как природных явлений: обер­тоновый ряд действительно дан природой звучащего тела, так как обертоны производятся делением звучащего тела на части. Унтерто­ны же, для того чтобы быть равноправными с обертонами природны­ми явлениями, должны бы получаться умножением (?!) массы зву­чащего тела, что абсурдно (умножение означает, что для извлечения звука нижней октавы, например, на струне необходимо длину стру­ны при вибрации увеличивать вдвое, что невозможно физически).

Несмотря на наличие еще ряда теорий мажора и минора (среди которых нужно упомянуть теории А. С. Оголевца и П. Н. Мещани­нова, см. с. 255), трудно назвать такую, которую можно было бы считать отвечающей на все вопросы. Вероятно, теория Царлино (вклю­чающая проблему мажора и минора в общую теорию эстетических пропорций) и теория Хауптмана (наилучшим образом обосновываю­щая смысловое содержание понятий мажора и минора) в их взаимо­дополнении дают наиболее надежную основу для верного понимания этого важнейшего явления музыки.

Дата добавления: 2015-06-27