Общая постановка задачи линейного программирования

ЧАСТЬ 1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Москва

РАБОЧАЯ ТЕТРАДЬ

ЧАСТЬ I

студент__1 курса ___________________________________________

___________________________________________________________

____________________________________________________________

группы №______

Экономико-математическая модель – это математическое описание исследуемого процесса или объекта экономики.

Построение модели включает три этапа:

1. выбор переменных задачи;

2. составление системы ограничений;

3. выбор целевой функции (критерия эффективности).

Переменные задачи – это величины, которые полностью характеризуют исследуемый процесс (объект). Переменные записываются в виде вектора .

Система ограничений – система уравнений или неравенств, которым удовлетворяют переменные задачи и которые следуют из физического или экономического смысла задачи.

Целевая функция – это функция переменных задачи, которая характеризует качество выполнения задачи и максимум или минимум которой требуется найти.

Если целевая функция и система ограничений линейные, то такая задача является задачей линейного программирования.

Общая постановка задачи линейного программирования:

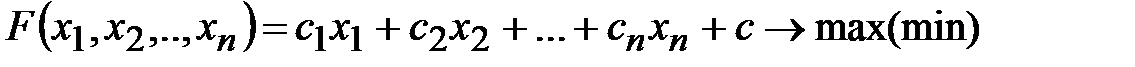
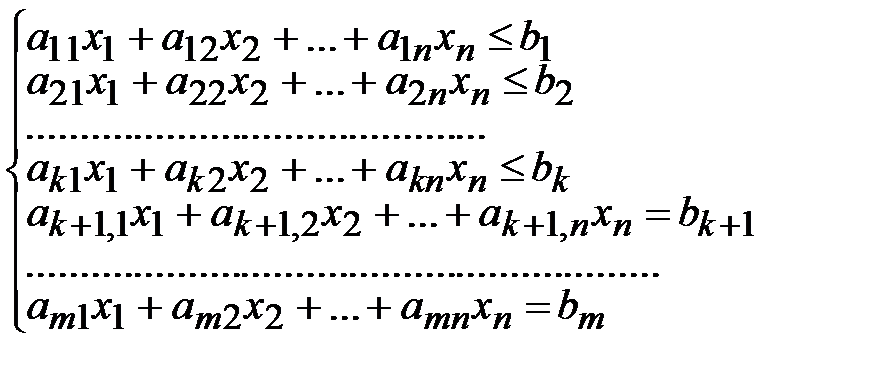
где 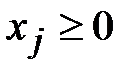, ( меняется от 1 до ).

Пример 1. При производстве двух видов продукции используется три вида сырья. Составить план выпуска продукции, обеспечивающий максимум прибыли. Исходные данные приведены в таблице.

Расход сырья на единицу продукции	Запасы сырья
№1	№2
		Прибыль

Решение. Пусть 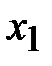и 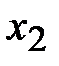- это объемы первой и второй продукции, которые необходимо выпускать.

Тогда 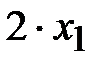- это расход первого сырья на производство первой продукции, - это расход первого сырья на производство второй продукции, - это расход первого сырья на производство первой и второй продукции вместе. Из таблицы видно, что запас первого сырья равен 21 единице. Понятно, что нельзя израсходовать сырья больше, чем есть в запасе, но можно израсходовать меньше сырья, если это выгодно. То есть - первое неравенство из системы ограничений. Аналогично можно составить неравенства для второго и третьего сырья и .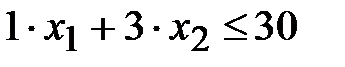

Если за реализацию единицы первой продукции можно получить прибыль , то 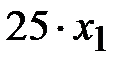- прибыль за реализацию всей первой продукции. Аналогично 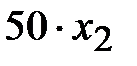- прибыль за реализацию всей второй продукции. Тогда - прибыль от реализации всей первой и второй продукции. Естественно, что любой предприниматель рассчитывает на наибольшую прибыль, то есть .

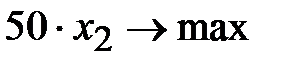Таким образом, экономико-математическую модель задачи можно записать в следующем виде:

.

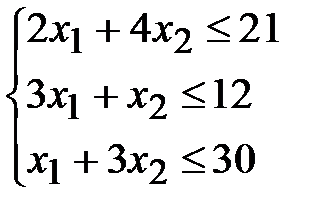
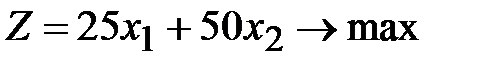Пример 2. В рационе животных используются два вида кормов. Животные должны получать три вида веществ. Составить рацион кормления, обеспечивающий минимальные затраты. Исходные данные приведены в таблице.

Содержание питательного вещества в единице корма	Необходимое количество питательного вещества
№1	№2
		Стоимость единицы корма

Решение. Пусть 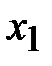и 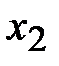- это объемы первого и второго кормов соответственно, которые необходимо использовать.

Тогда - это объем первого питательного вещества в первом корме, 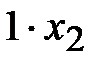- это объем первого питательного вещества во втором корме,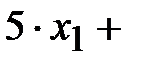 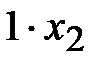- это объем первого питательного вещества в первом и втором корме вместе. Из таблицы видно, что необходимое для нормального развития количество первого питательного вещества равно 15 единицам. Понятно, что животные не должны получать питательных веществ меньше необходимого количества, но большее количество им не повредит. То есть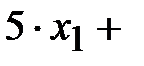 - первое неравенство из системы ограничений. Аналогично можно составить неравенства для второго и третьего питательных веществ 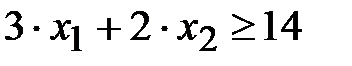и .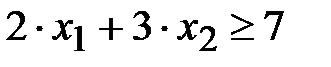

Если единица первого корма обходится в 40, то - затраты на приобретение всего первого корма. Аналогично - затраты на приобретение всего второго корма. Тогда - общие затраты. Естественно, что любой предприниматель рассчитывает на минимальные затраты, то есть .

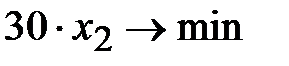Таким образом, экономико-математическую модель задачи можно записать в следующем виде:

.

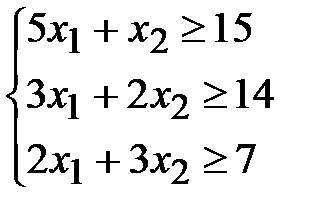
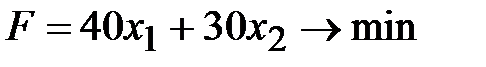Задания для решения в аудитории

1. Для изготовления шкафов и столов отделочный завод использует шесть видов древесины. Исходные данные приведены в таблице. Составить план выпуска продукции так, чтобы липу и ель израсходовать полностью и обеспечить минимум затрат.

Виды древесины	Шкафы	Столы	Запасы
Береза	0,25		6,24
Сосна	0,5	0,75	4,75
Дуб
Кедр	0,4
Липа	0,35	0,21	11,1
Ель	0,5	0,25	8,2
Затраты			-

2. Для изготовления тортов и пирожных используются пять видов кондитерских добавок. Исходные данные приведены в таблице. Составить план выпуска продукции так, чтобы сахарная пудра и разрыхлитель израсходовать полностью и обеспечить максимум прибыли.

Виды добавок	Торты	Пирожные	Запасы
Ванилин
Кокосовая стружка
Какао
Сахарная пудра	0,25	0,25
Разрыхлитель	0,45	0,21
Прибыль			-

Дата добавления: 2015-06-27