КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Переход от канонической формы задачи линейного программирования к стандартной форме
|
|
|
|
Переход от канонической формы к стандартной форме задачи линейного программирования можно выполнить по следующему правилу:
1. Из коэффициентов при неизвестных и свободных членов уравнений системы ограничений и целевой функции составляется матрица. Коэффициенты целевой функции записываются в последнюю строку матрицы, на месте свободного члена записывается ноль.
2. Методом Жордана - Гаусса матрица приводится к разрешенному виду. При вычислениях разрешающий элемент в последней строке выбирать нельзя.
3. Составляется система уравнений из полученной разрешенной матрицы.
4. Базисные переменные в системе ограничений отбрасываются. При этом если переменная входила в уравнение со знаком 
, то в соответствующем уравнении ставится знак 
, если со знаком 
, то ставится знак 
.
5. Если целевая функция на максимум, то в системе ограничений все неравенства со знаком умножить на 
, если на минимум, то умножить неравенства со знаком .
Пример 4. Привести к стандартному виду задачу линейного программирования.
, 
, 
.
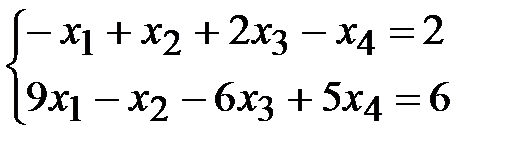
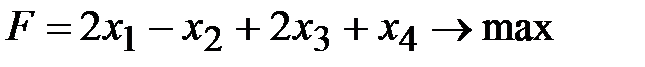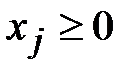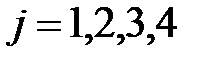Решение. Из системы ограничений и целевой функции составим расширенную матрицу. Для наглядности запишем матрицу в виде таблицы. 
| Строки |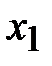 
| 
| 
| 
| 
|
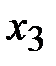
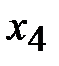
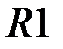
| -1 | -1 | |||
| -1 | -6 | |||
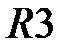
| -1 |
Методом Жордана - Гаусса приведем полученную матрицу к разрешенному виду. Для этого выберем в первой строке разрешающий элемент, например . Выполним действия 
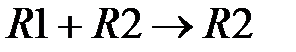и 
.
| Строки |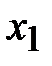
|
|
|
|
|
|
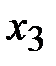
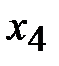
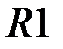
| -1 | -1 | |||
|
| -4 | ||||
|
|
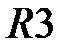
Разделим всю вторую строку на 
.
| Строки |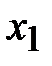
|
|
|
|
|
|
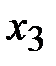
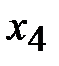
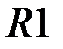
| -1 | -1 | |||
|
| -2 | -1 | -2 | ||
|
|
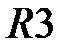
Выберем во второй строке разрешающий элемент, например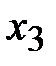 
. Выполним действия 
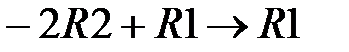и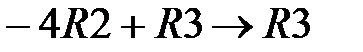 
.
| Строки |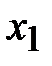
|
|
|
|
|
|
| |||||
|
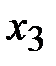
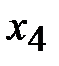
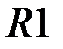
| -2 | -1 | -2 | ||
|
|
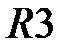
Составим из полученной матрицы систему ограничений и целевую функцию. При этом цифру из правого нижнего угла таблицы записываем с противоположным знаком в целевую функцию.
, , .
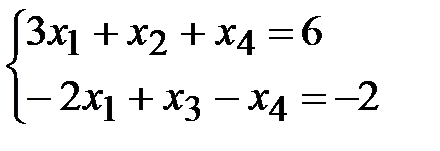
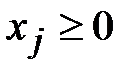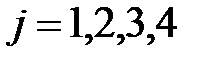Разрешающие переменные входят в систему ограничений со знаком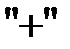 
, значит их можно отбросить, а знак 
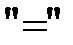заменить на знак 
.
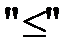Стандартный вид исходной задачи:
, , 
.
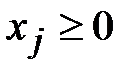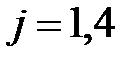Задания для решения в аудитории
1. Привести к стандартному виду задачу линейного программирования.
, , 
.
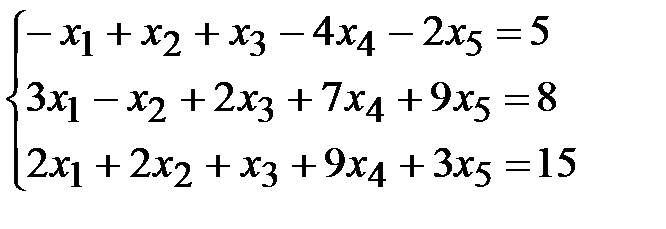
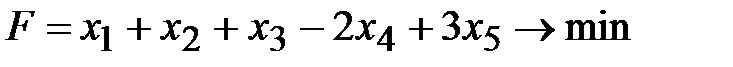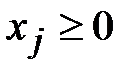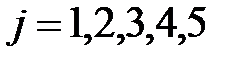Задания для самостоятельной подготовки
1. Привести к каноническому виду задачу линейного программирования.
, , 
.
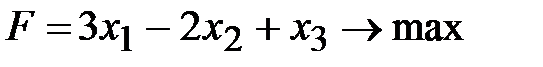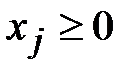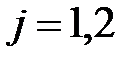2. Привести к стандартному виду задачу линейного программирования.
, , .
|
|
|
|
|
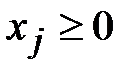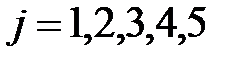Дата добавления: 2015-06-27; Просмотров: 4168; Нарушение авторских прав?; Мы поможем в написании вашей работы!