Метод искусственного базиса

Данный метод применяется, если в задаче линейного программирования сразу не получилось начальное допустимое базисное решение.

Пусть имеется каноническая задача линейного программирования:

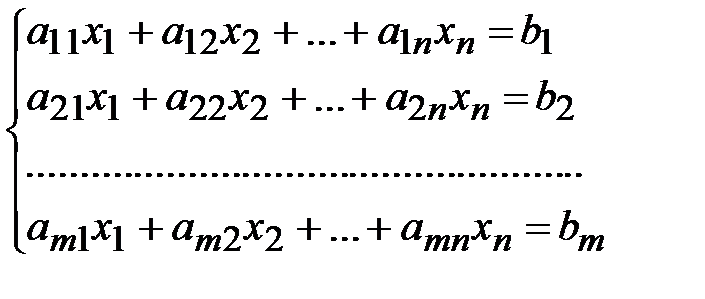
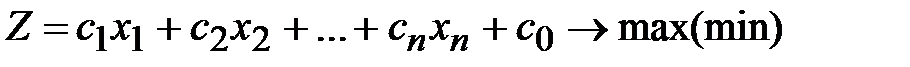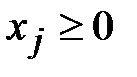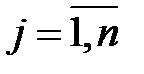, , и , .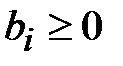

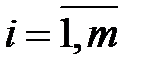Алгоритм метода искусственного базиса:

1. К левым частям уравнений системы ограничений, из которых появляются отрицательные компоненты в базисном решении, прибавляются искусственные переменные 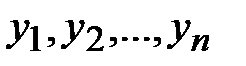, которые выбираются в качестве базисных:

.

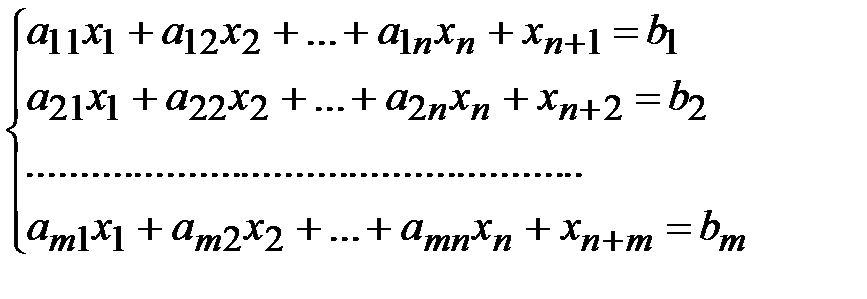Искусственные переменные могут быть введены в одно, несколько или все уравнения системы ограничений.

2. В целевую функцию эти искусственные переменные в задаче на максимум вводятся с коэффициентом 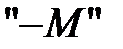, а в задаче на минимум с коэффициентом 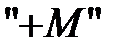, где 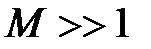- число намного большее единицы.

3. Записывается новая целевая функция:

,

.

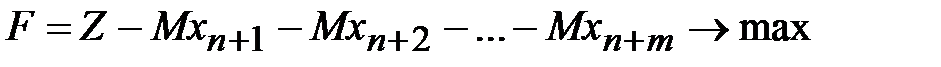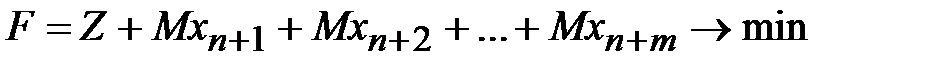После подстановки выражений искусственных переменных из системы ограничений в выражения для 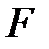и приведения подобных выражения новой целевой функции могут быть записаны в виде:

,

.

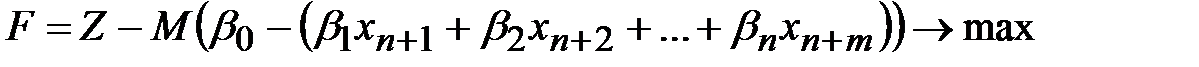4. В симплексную таблицу целевая функция записывается в виде двух строк 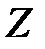и 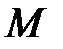. Для задачи на максимум в строку для 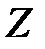записываются коэффициенты , в строку для 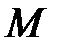коэффициенты .

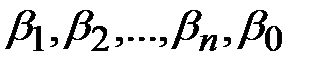5. При переходе искусственных переменных из числа базисных в число свободных столбцы, соответствующие этим искусственным переменным в каждой последующей симплексной таблице вычеркиваются.

6. Чтобы определить разрешающий столбец в задаче на максимум, в строке функции 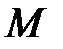выбирается наибольший положительный элемент. Ему соответствует разрешающий столбец.

7. Разрешающая строка определяется как в обычном симплексном методе.

8. После перехода всех искусственных переменных 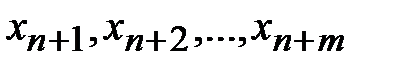из числа базисных в число свободных, будет получено допустимое решение. При этом строка 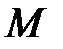должна получиться нулевой.

9. Дальше задача решается обычным симплексным методом.

Пример 9. Решить задачу линейного программирования методом искусственного базиса:

,

, , .

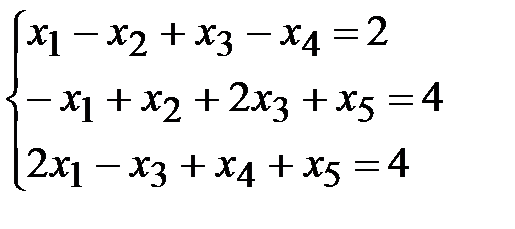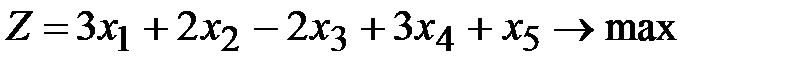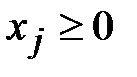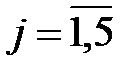Решение.

1. Задача приведена к каноническому виду. Для системы ограничений соответствует матрица: 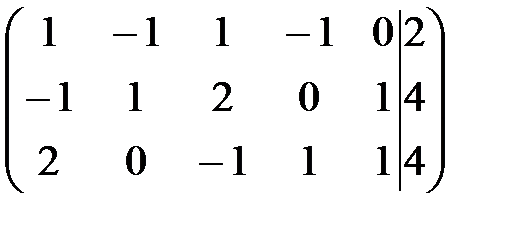. Как видно из матрицы система ограничений не приведена к допустимому виду.

2. Введем искусственные переменные в систему ограничений:

.

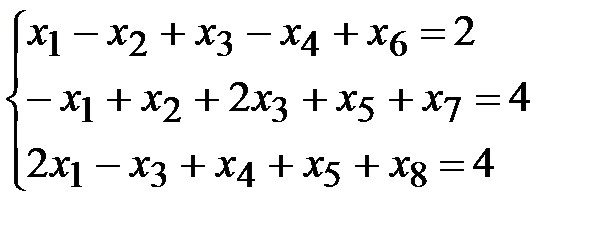3. Запишем новую целевую функцию:

.

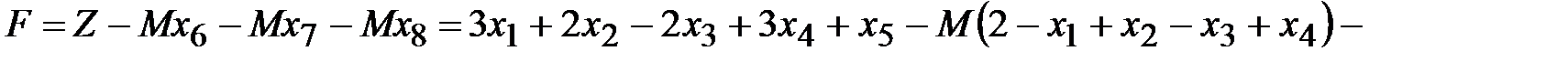
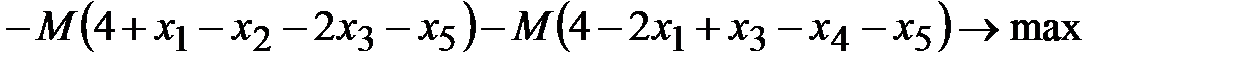Приведем подобные и запишем:

.

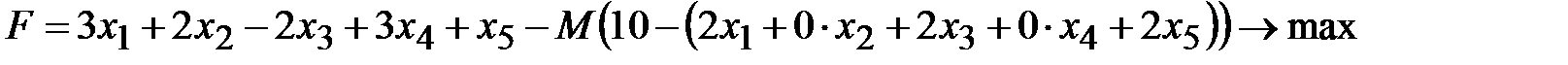4. Составим симплексную таблицу. Так как в последней строке все положительные элементы одинаковые, выберем любой, например, первый. Тогда столбец 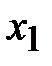разрешающий. Оценки 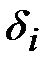для первой и третьей строки одинаковые, поэтому в качестве разрешающей возьмем любую, например, первую. Тогда 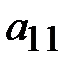- разрешающий элемент.

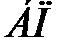
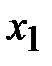
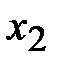
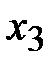
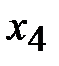
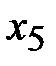
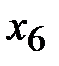
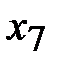
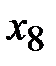
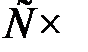
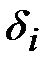
		-1		-1
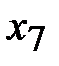
	-1
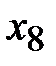
			-1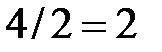
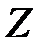
			-2

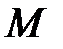
Выполним действия: 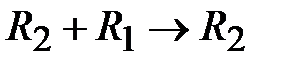, , 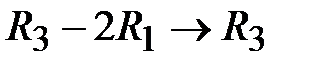, 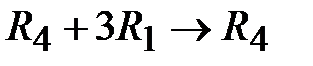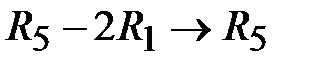. При этом искусственная переменная 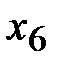становится свободной, а 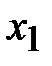- базисной. Столбец искусственной переменной 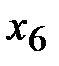в новой таблице можно исключить.

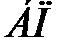
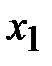
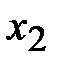
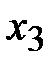
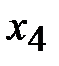
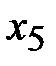
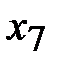
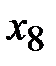
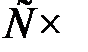
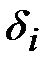
		-1		-1
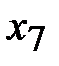
				-1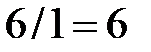
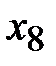
			-3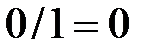
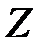
			-5					-6

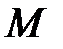
Выполним действия: 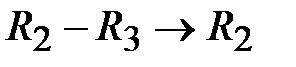, , 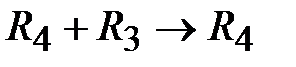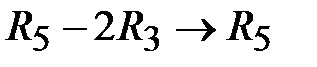. При этом искусственная переменная 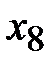становится свободной, а 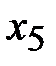- базисной. Столбец искусственной переменной 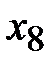в новой таблице можно исключить.

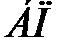
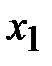
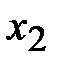
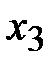
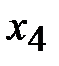
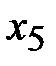
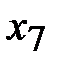
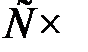
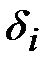
		-1		-1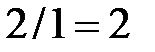
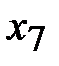
		-2		-4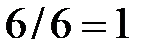
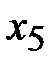
			-3					-
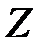
			-2				-6
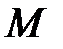
		-2		-4

Разделим вторую строку на 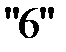, чтобы разрешающий элемент был равен единице. После деления на 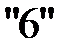выполним действия: 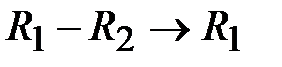, , 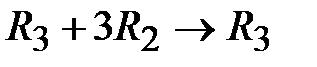, 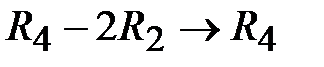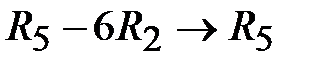. При этом искусственная переменная 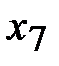становится свободной, а 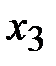- базисной. Столбец искусственной переменной 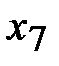в новой таблице можно исключить.

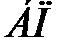
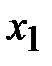
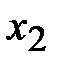
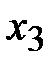
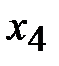
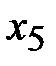
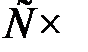
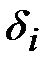
		-2/3		-1/3
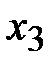
		-1/3		-2/3
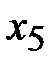
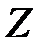
		7/3		5/3		-4

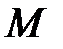
Последнюю строку можно вычеркнуть. Таким образом, получено начальное допустимое решение 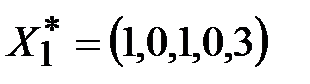, при котором .

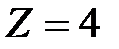4. Дальше применяем обычный симплексный метод. Выполним действия: 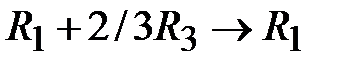, , 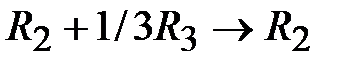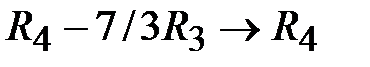. Переменная 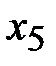становится свободной, а - базисной.

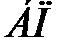
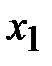
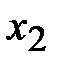
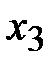
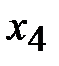
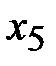
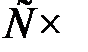
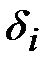
				1/3	2/3
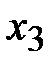
				-1/3	1/3
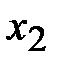
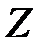
				-2/3	-7/3	-11

В последней строке коэффициенты при свободных переменных 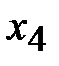и 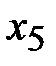отрицательные, следовательно, оптимальное решение найдено: 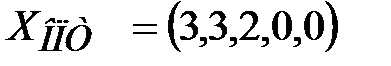и .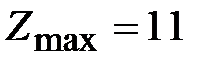

Пример 10. Решить задачу линейного программирования методом искусственного базиса:

, , , .

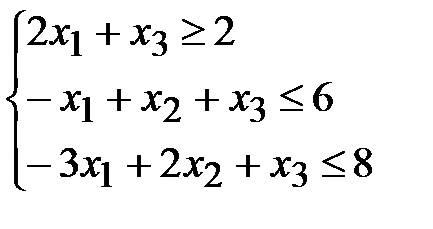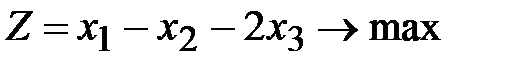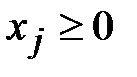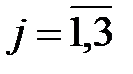Решение.

1. Приведем задачу к каноническому виду. Введем балансовые переменные: .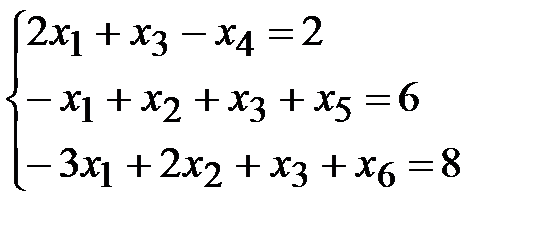

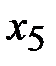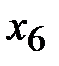2. Балансовые переменные и могут быть выбраны в качестве базисных. Переменная 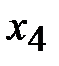не совпадает по знаку со свободным членом.

3. Введем в первое уравнение искусственную переменную:

.

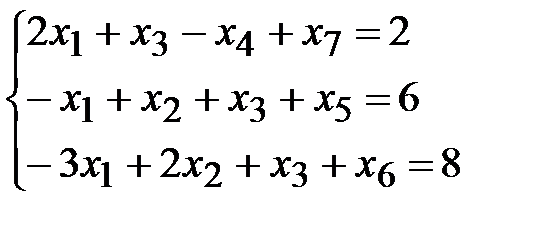4. Запишем новую целевую функцию:

или

.

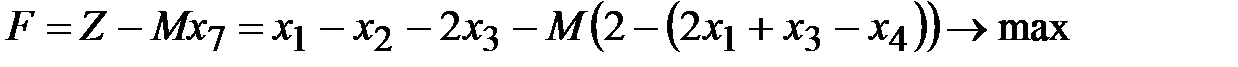5. Составим симплексную таблицу. В последней строке наибольший положительный элемент находится в первом столбце. Столбец 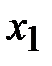разрешающий. В разрешающем столбце положительный элемент есть только в первой строке, поэтому оценки 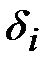находить не надо. Первая строка – разрешающая.

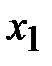
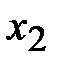
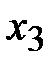
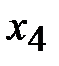
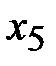
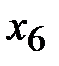
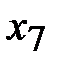
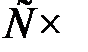
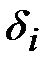
				-1
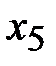
	-1
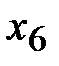
	-3
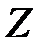
		-1	-2
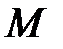
				-1

Разделим первую строку на 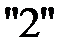, чтобы разрешающий элемент был равен единице. После деления на 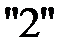выполним действия: 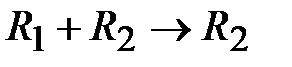, , 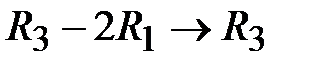, , 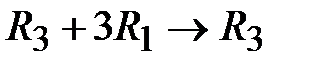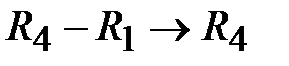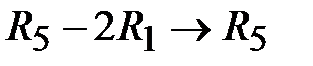. При этом искусственная переменная становится свободной, а 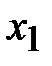- базисной. Столбец искусственной переменной 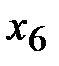в новой таблице можно исключить.

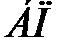
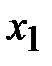
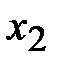
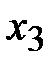
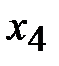
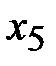
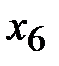
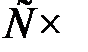
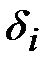
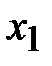
			1/2	-1/2
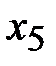
			3/2	-1/2
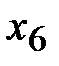
			5/2	-3/2
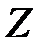
		-1	-5/2	1/2			-1

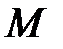
Последнюю строку можно вычеркнуть. Таким образом, получено начальное допустимое решение: , .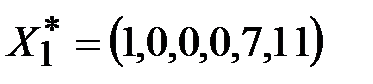

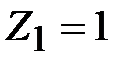6. Дальше применяем обычный симплексный метод. В строке целевой функции 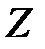положительный элемент есть только в столбце 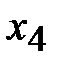. Это разрешающий столбец. При этом в разрешающем столбце нет положительных элементов. Следовательно, задача оптимального решения не имеет и .

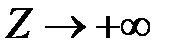Задания для решения в аудитории

Решить методом искусственного базиса задачу линейного программирования:

1. , , , .

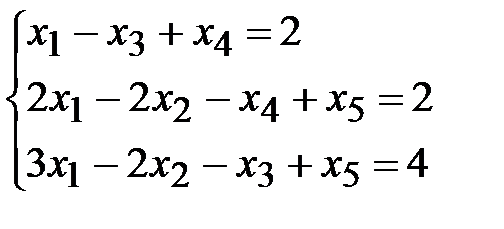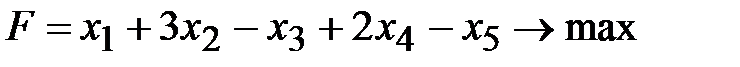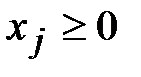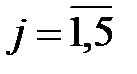2. , , , .

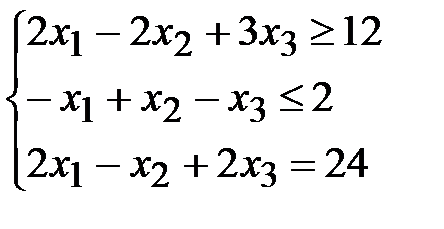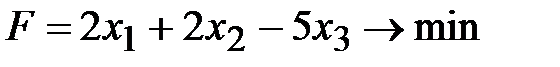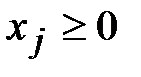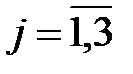Задания для самостоятельной подготовки

1. Решить задачи линейного программирования методом искусственного базиса , :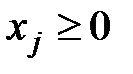

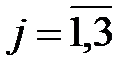1.1. , , , .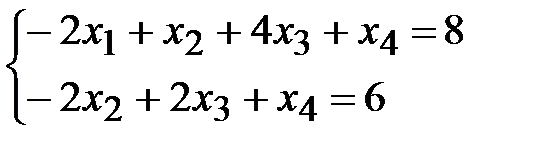

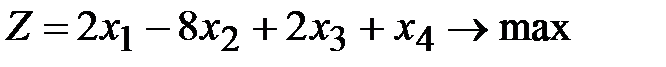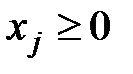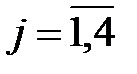1.2. , , , .

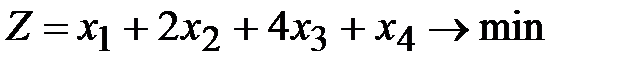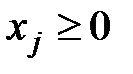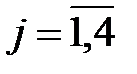1.3. , , , .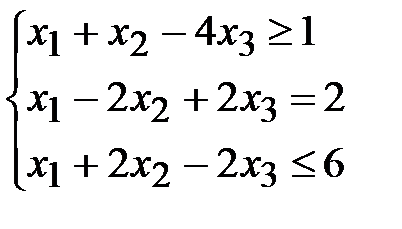

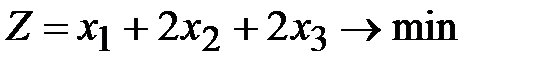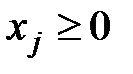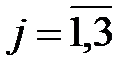1.4. , , , .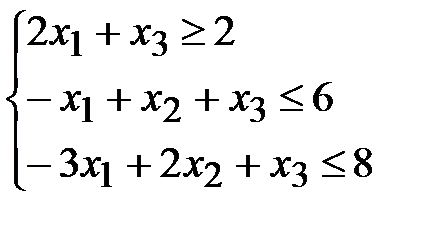

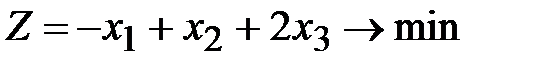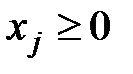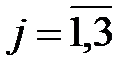Ответы: 1.1. 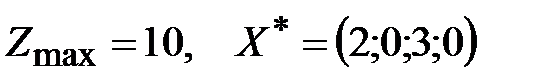. 1.2. Система ограничений несовместна. 1.3. , , 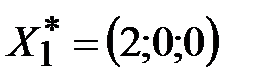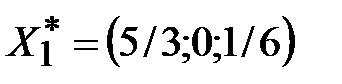. 1.4. Оптимального решения нет, .

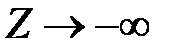Дата добавления: 2015-06-27