Интерполяционные многочлены Лагранжа и Ньютона

Задача интерполяции заключается в следующем. На отрезке [ a, b ] заданы упорядоченные n+ 1 точки и значения функции в этих точках, т. е. задана таблица значений функции :

				…
				…

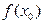
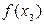
Требуется найти значения этой функции для промежуточных значений аргумента, не совпадающих с приведенными в таблице. Получить аналитическое выражение функции по таблице ее значений в большинстве случаев невозможно. Поэтому вместо нее строят другую функцию , которая легко вычисляется и имеет ту же таблицу значений, что и , т. е. ; Исходная функция называется интерполируемой функцией, а функция – интерполяционной. Значения аргумента в таблице называются узлами интерполяции.

В общем случае полином степени n, принимающий при х = х_i заданные значения y_i (i= 0, 1,…, n), можно представить интерполяционной формулой Лагранжа

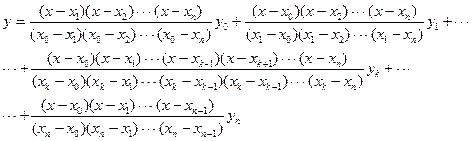
Пусть разности табличных значений аргумента – постоянные (шаг таблицы). Тогда значение функции y для промежуточных значений х приближенно можно найти при помощи интерполяционной формулы Ньютона

где последовательные конечные разности функции y.

Для удобства пользования формулой Ньютона рекомендуется предварительно составить таблицу конечных разностей.

При х = х_i полином Ньютона принимает соответственно табличные значения y_i.

Погрешность интерполяционной формулы Ньютона приближенно можно оценить по формуле

.

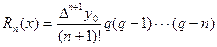Если число n можно взять любым, то его следует выбирать так, чтобы разность 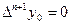в пределах данной точности; иными словами, разности 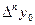должны быть постоянными в заданных десятичных разрядах.

Пример. Найти 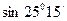, пользуясь табличными данными .

i	xi	yi	∆ yi	∆ ^2yi
	26^0	0,43837		-14
	27^0	0,45399
	28^0	0,46947

Здесь 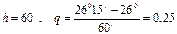. Применяя формулу Ньютона, используя первую горизонтальную строку таблицы, имеем 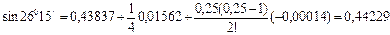. Причем погрешность 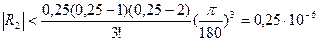. Таким образом, все полученные знаки ─ верные.

Дата добавления: 2015-06-27