IЧастичная O

A(контрарность) E

П П

о о

д д

ч ч

и Противо- речие и

н н

е е

н н

и и

е е

совместимость

(субконтрарность, перекрещивание)

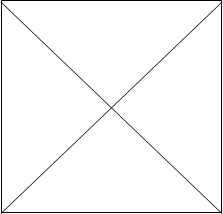
Верхняя сторона есть отношение между А и Е - противоположность (контрарность); нижняя сторона - отношение между I и O - частичная совместимость (субконтрарность); две вертикальные стороны - отношения между А и I (левая), Е и О (правая) - подчинение; диагонали - отношение между А и О, Е и I - противоречие (контрадикторность). На изображении “логического квадрата” совместимые отношения обозначены непрерывной линией, несовместимые - прерывистой.

§3. Операции с простыми категорическими суждениями (непосредственные умозаключения)

Логические операции с простыми категорическими суждениями - это такие их преобразования, в результате которых из исходного суждения определенного типа (A, E, I, O) получаются суждения других типов. При этом, зная значение истинности исходного суждения, мы можем делать определенные выводы о значении истинности результирующего. Поэтому такие преобразования часто относят к дедуктивным умозаключениям (непосредственные заключения из одной посылки). С их помощью мы уточняем и выражаем яснее свои мысли, находим новые оттенки последних, делаем неявное знание явным.

В качестве простейших преобразований простого категорического суждения можно рассматривать изменение его качественной и количественной характеристик и получение из суждения одного из типов суждений всех остальных типов с теми же терминами. При этом все они связаны только что рассмотренными соотношениями “логического квадрата” и значения истинности результарующих суждений в большинстве случаев однозначно определяются значением истинности исходных, что отражено в табл. 1 (“?” означает неопределенность истинности). Это так называемые “умозаключения по логическому квадрату”.

Таблица 1.

Вид посылки	Вид заключения и его значения, полученного из отношения
и ее значение	а) противоречия	б) противопо-ложности	в) перекрещива-ния	г) подчинения
Аи Ал Еи Ел Iи Iл Ои Ол	Ол Ои Iл Iи Ел Еи Ал Аи	Ел Е? Ал А? - - - -	- - - - О? Ои I? Iи	Iи I? Ои О? А? Ал Е? Ел

Более сложными операциями являются обращение, превращение и противопоставление.

Обращение - это смена ролей терминов исходного суждения (субъект S исходного становится предикатом результирующего, а предикат Р исходного - субъектом результирующего) без изменения качества.

Различают обращение с ограничением, когда из общего суждения выведено частное, и обращение без ограничения (или прямое) без потери количества. В частном случае выделяющих утвердительных суждений обращение дает не только из общего общее, но и общеутвердительное из частноутвердительного. Такой характер обращения связан с нераспределенностью предиката утвердительных суждений в общем случае и его распределенностью в выделяющих суждениях (см. примеры).

Превращение - логическая операция изменения качества исходного суждения и замены его предиката на противоречащий, количественная характеристика не меняется.

3. Противопоставление - логическая операция, состоящая в последовательном осуществлении двух рассмотренных. Различают противопоставление субъекту, которое получается превращением результата обращения исходного суждения, и противопоставление предикату - обращение результата превращения исходного. Это вполне самостоятельная и оригинальная по результату операция, хотя она и является комбинацией двух других.

Характер результатов проведения всех этих четырех операций в зависимости от типа преобразуемого суждения (посылки непосредственного умозаключения) отражежен в табл. 2.

Таблица 2.

Вид	результата (заключения), полученного путем
посылки	обращения	превращения	противопоставления субъекту	противопоставления предикату
Аесли Р(-) если P(+)	I (PS) А (PS)	E (S ~P) E (S ~P)	O (P ~S) E (P ~S)	E (~PS) Е (~ РS)
E	E (PS)	А (S ~P)	A (P ~S)	I(~PS)
I если P(-) если P(+)	I (PS) A (PS)	O (S ~P) O (S ~P)	O (P ~S) E (P ~S)	не противопоставляется
О	не обращается	I (S ~P)	не противопоставляется	I (~PS)

Символы в скобках указывают местоположение терминов посылки в заключении (РS). Знак отрицания перед термином указывает на то, что берется его дополнение (Р - “смертный”, ~ Р - “бессмертный”). Знаки “+” и “-” обозначают соответственно распределенность и нераспределенность термина.

Примеры. Проделаем операции обращения, превращения и противопоставления для общего и частных случаев утвердительных суждений.

Исходное суждение: “Все металлы (S) электропроводны (P)”. Тип A, все операции возможны. Обращение: “Некоторые электропроводные (вещества) – металлы” (I); Превращение: “Ни один металл не является неэлектропроводным” (E); Противопоставление субъекту: “Некоторые электропроводные (вещества) не является неметаллами” (O); Противопоставление предикату: “Ни одно неэлектропроводное (вещество) не является металлом” (E)

Круговая диаграмма P S   ~P

Исходное суждение: “Все квадраты (S) - прямоугольные ромбы (P)”. Тип A - общеутвердительное выделяющее суждение, все операции возможны. Обращение: “Все прямоугольные ромбы - квадраты” (A) Превращение: “Ни один квадрат не является непрямоугольным ромбом” (E) Противопоставление субъекту: “Ни один прямоугольный ромб не является неквадратом” (E) Противопоставление предикату: “Ни один непрямоугольный ромб не является квадратом” (E)

Круговая диаграмма B S, P   где B - ромб

Исходное суждение: “Некоторые учащиеся (S) - студенты (P)”. Тип I, выделяющее суждение. Обращение: “Все студенты - учащиеся” (A) Превращение: “Некоторые учащиеся не являются нестудентами” (O) Противопоставление субъекту: “Ни один студент не является неучащимся” (E) Противопоставление предикату: “Некоторые нестуденты не являются учащимися” (O).

Круговая диаграмма S   P

Отметим, что неосуществимость обращения суждений типа O связана с неопределенностью соотношения субъекта и предиката в общей форме такого суждения. Соответственно и операции противопоставления считаются неосуществимыми в обозначенных в таблице случаях, поскольку связаны с необходимостью проводить обращение таких суждений. Однако в частном случае исходного выделяющего частноутвердительного суждения определенности вполне достаточно для его противопоставления предикату и полученный в последнем примере результат вполне правомерен.

Литература

1. Кобзарь В.И. Основы логических знаний: Учеб. для студ. гум. фак-тов. Гл.3. СПб.: Изд-во СПб ун-та, 1994. С. 39 - 47, 54 - 59.

2. Логика: Учеб. пособие / Под ред. Б.В.Ахлибининского / ГЭТУ. Гл.II. СПб, 1995. С. 21 - 31.

3. Основные законы и формы мышления: Логический практикум / Под ред. М.Ю.Казаринова / ГЭТУ. Гл. II. СПб, 1997. С. 18 - 27.

Лекция 6. Суждение (продолжение)

Дата добавления: 2015-06-27