Нечеткие знания

Наиболее нормальным свойством человеческого интеллекта является способность принимать правильные решения в области неполной и нечеткой информации. Существует целый класс описаний, оперирующих качественными характеристиками объекта, к примеру:

¾ Красивая прическа

¾ Очень сильный и т.д.

Эти характеристики обычно размыты и не могут быть однозначно интерпретированы однако содержат важную информацию. Кроме того, в задачах, решаемы[ интеллектуальными системами, приходится пользоваться неточными знаниями, которые не могут быть интерпретированы, как полностью истинные или ложные. Существуют знания, достоверность которых выражается, некоторой,промежуточный цифрой, например 0,7.

Как не разрушая свойств различности таких знаний представить их формально?:

Для решения таких проблем американский математик Лотфи Заде предложил формальный аппарат нечетко (fuzzy) алгебры и нечеткой логики. Позднее это направление получило широкое распространение. (Орловский 1981 г.; Оверкин 1986 г.; Яшин 1990 г.) и положило начало одной из ветвей искусственного интеллекта под названием мягкие вычисления soft cjmputing Лотфи Заде ввел одно из главных определений нечеткой логики:

Лингвистическая переменная - это переменная, значение которой определяется набором вербальных, т.е. словесных характеристик некоторого свойства.

Пример: лингвистическая переменная (рост) определяется через набор значений:

¾ Карликовый

¾ Низкий

¾ Средний

¾ Высокий

¾ Очень высокий

Лотфи Заде отмечал, что изменение стремление к точности в современных системах управления привело к тому, что эти системы становятся слишком сложными и неработоспособными, в виду снижения динамической устойчивости. Для решения проблемы,мы должны отказаться от таких проблем, которые являются нечеткими и размытыми.

Нечеткое множество - пусть Е - универсальное множество

Х – элемент Е

R- некоторое свойство

Обычно четкое подмножество А универсального множества У элементы которого удовлетворяю свойству R определяется, как множество упорядоченных пар:(/- не деление)

A={µ_a(x)/x}, где

µ_а(x)- характеристическая функция или функция принадлежности, принимающее значение 1, если х удовлетворяет свойству R и 0 в противном случае.

Нечеткое подмножество отличается тем, что функция принадлежности µ_а(x) может принимать значения не только {0;1} но и некоторое промежуточное µ=[0,1], где µ называют множеством принадлежности, если µ={0,1} (можем взять либо 0,либо 1)

Примеры записей нечеткого множества:

E={x₁, x₂, x₃, x₄, x₅}

А-нечеткое множество для которого

µ_а(x₁)=3

µ_а(x₂)=0

µ_а(x₃)=1

µ_а(x₄)=0,5

µ_а(x₅)=0,9

Тогда А можно представить в виде А=0,3/х₁+0/x₂+1/х₃+0,5/х₄+0,9/х₅

Здесь знак + знак объединения.

Или А={0,3/х₁ ;0/x₂;1/х₃;0,5/х₄;0,9/х₅}

Основные характеристики нечетких множеств:

µ=[0,1]

sup µ_а(x)- высота нечеткого множества А и означает четкую верхнюю границу.

x принадлежит E

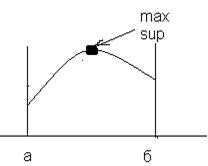
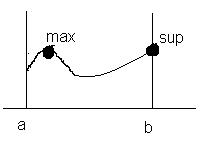
Нечеткое множество нормально, если его высота равна 1.

Если sup µ_а(x)<1, х принадлежит Е множество субнормально.

Если для любого х принадлежащего E, µ_а(x)=0? То нечеткое множество пусто.

Не пустое и sup-нормальное множество можно нормализовать по формуле:

µ_а(x)= µ_а(x)/ sup µ_а(x), x принадлежит E

Нечеткое унимодально, если µ_а(x)=1, только для одного х из E.

Точка перехода- это элементы x, принадлежащие E для которых µ_а(x)=0,5.

Примеры нечетких множеств:

1 пример). Пусть Е={0,1,2,3…..10}; µ=[0,1], при этом множество принадлежности непрерывно от 0 до1. Нечеткое множество “несколько” можно определить следующим образом:

“ несколько”=0,5/3+0,8/4+1/5+1/6+0,8/7+0,5/8

Характеристики:

Высота-1

Точки перехода-3,8

Носитель нечеткого множества (тех для которых µ_а(x)>0: называют сами 3,4,5,6,7,8)

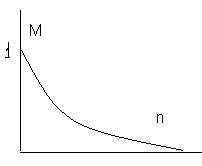
2 пример). Пусть Е={0,1,2,…n₁….};

Нечеткое множество “малый” можно определить следующем образом

µ“малый”(n)=1/(1+(n/10)²)=1(приблизительно)

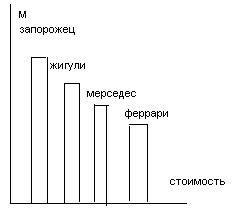
3 пример).Пусть Е={Запорожец, Жигули, Мерседес, Феррари…..};

E^/=[0,¥]- универсальное множество (стоимость). Тогда на E^/ мы можем определить нечеткие множество типа “ для бедных”;” для среднего класса”;

“престижность” с функциями принадлежности, показанными на рисунке:

Имея эти функции и зная стоимость автомобилей из E^/ большое мы тем самым определим на E^/ нечеткие множества с этими же названиями. Так, например нечеткое множество “для бедных” заданное на множестве марок автомобилей выглядит так, как показано на рисунке.

Дата добавления: 2015-06-27