Методы построения функции принадлежности нечетких множеств

Методы можно разделить на прямые и косвенные: в прямых методах эксперт либо просто задает для каждого x принадлежащее E- значения m_а(x), либо определяет функции совместимости.

Прямые методы используют обычно для измеримых понятий (скорость, время, расстояние) или когда выделяются полярные значения.

Для многих практических задач можно выделить набор признаков и для каждого определить полярные значения функции принадлежности: 0 и 1.

Например: в задаче распознавания лиц можно выделить шкалы, приведенные в таблице:

Признаки
X1	Высота лба	Низкий лоб	Широкий
X2	Длина носа	Короткий	Длинный
X3	Цвет лица	темный	светлый

Для конкретного лица А эксперт из приведенной шкалы задает m_а(x) принадлежащее {0,1}, формируя векторную функцию принадлежности:{ m_а(x₁),m_а(x₂), m_а(x₃)} Результаты экспертов усредняются и формируются в функции принадлежности со значениями от 0 до 1 m_а(x) принадлежащее [0,1]. При прямых методах – групповые прямые методы используются достаточно часто.

Косвенные методы - определение функции принадлежности в случаях, когда нет элементарных измеримых свойств.

Если бы значение функции принадлежности были бы известны, например m_а(x)=W_i, i=1…n, то используя метод попарных сравнений можно получить матрицу отношений:

А={a_i,j}, где a_i,j=w_i/w_j

На практике эксперт сам формирует матрицу А, при этом диагональные элементы равны 1, а элементы симметричны относительно диагоналям.

a_i,j= 1/a_i,j

_®

В общем случае задача сводится к поиску вектора W, получаем уравнение вида:

_{® ®}

A* W=l_max*W, где

l_max- наибольшее собственное значение матрицы A. Собственное число находится решением уравнения:

/A-l*E/=0

Можно выделить еще два подхода:

1) Использование относительных частот по данным эксперимента в качестве значений функций принадлежности, то есть на основе обработке статистических данных.

2) Использования типовых форм функции принадлежности с уточнением их параметров по результатам экспериментов.

Часто используются так называемые функции принадлежности в форме (L-R) типа, где L- левая, R-правая.

Указывает крутизну 1 и 2 шага.

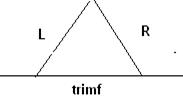
Операции над нечеткими множествами:

1. Пересечение- AÇB- наиболее нечеткое подмножество, содержащееся одновременно в A и B

m_аÇb(x)= min (m_a(x),m_b(x))

2. Объединение- AÈB- наименьшее нечеткое подмножество, включающее, как A так и B с функцией принадлежности

m_аÈb(x)= max (m_a(x),m_b(x))

Дата добавления: 2015-06-27