Алгоритм TsuKamoto

Алгоритм Mamdani.

Данный алгоритм соответствует примеру и рисунку 1. В рассматриваемой ситуации он может быть математически описан следующим образом:

1. нечеткость: находятся в степени истинности для предпосылок каждого правила: A1(x₀),A2(x₀),B1(y₀),B2(y₀₎)

2. нечеткий вывод: находятся уровни отсечения для предпосылок

каждого из правил с использованием операции min-мум.

α₁=А1(x₀)۸ B1(y₀),

α₂=А2(x₀)۸ B2(y₀),

Затем находятся усеченные функции принадлежности:

С₁′(z)= α₁۸C₁(z)

С₂′(z)= α₂۸C₂(z)

3. Композиция с использованием операции max-мум происходит объединение найденных усеченных функций, что приводит к получению четкого вывода с функцией принадлежности.

µ_∑(z)=C(z)= С₁′(z)٧ С₂′(z)

4.дефазикация, например центроидным методом для получения z₀.

Исходники, как и у предыдущего алгоритма, но функции С₁ и С₂ являются монотонными.

1-й этап: как и в алгоритме Mamdani уровни отсечения α₁ и α₂, а затем посредством решения уравнений

α₁= С₁(z)

α₂= С₂(z)

Определяются четкие значения z₁ и z₂ для каждого из исходных правил определяется четкое значение переменной вывода по формуле:

Z₀=(α₁*z₁+ α₂*z₂)/ (α₁+ α₂)

Что представляет собой дискретный вариант центроидного метода:

Z₀=(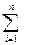 α_i*z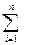_i)/ α_i

Пример:

Пусть имеем:

A1(x₀)=0,7; A2(x0)=0,6

B1(y₀)=0,3; B2(y₀)=0,8

α₁=min(A1(x₀)=0,7,B1(y₀))=min(0,7;0,3)=0,3

α₂=min(A2(x₀)=0,7,B2(y₀))=min(0,6;0,8)=0,6

и значения z1=8 и z2=4, найденных в результате решения уравнений С1(z1)=0,3; С2(z2)=0,6

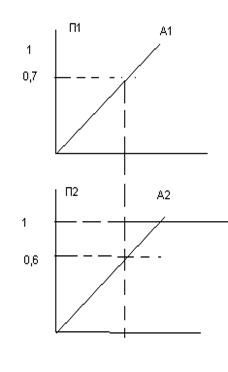Смотри рисунок 2.

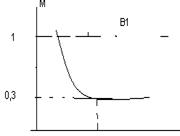
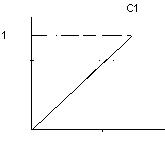
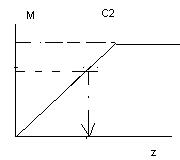
Рисунок 2.

Четкое значение переменной вывода:

Z₀=(8*0,3+4*0,6)/(0,3+0,6)

Z₀=5,3

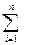W_i/N=1

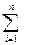W_i=1

Wi=1/K_i

K- ваши предположения.

Дата добавления: 2015-06-27