Операции над нечеткими отношениями

1. Объединение двух отношений R1 и R2 обозначается R1ÈR2 и определяется выражением µ R1ÈR2(х,у)= m_R1(x,у) È m_R2(x,у)

2. Пересечение двух отношений R1 и R2 обозначается R1ÇR2 и определяется выражением µ R1ÇR2(х,у)= m_R1(x,у) Ç m_R2(x,у), т.е. операция “взятия” минимума

3. Алгебраическое произведение 2х отношений R1 и R2 обозначается R1·R2 и определяется выражением µ R1·R2(х,у)= m_R1(x,у) · m_R2(x,у)

4. Дополнение отношения

m_R(x,у)= 1- m_R (x,у)

5. Композиция (свертка) двух нечетких отношений.

Пусть R1 нечеткое отношение из х и у между х и у R1:(х´у) [0,1] и R2 нечеткое отношение из y,z между y и z R2:(у´z) [0,1]

Нечеткое отношение между X и Z, обозначаемое R1○R2, определяемое через R1 и R2 выражением µ R1○R2(х,z)= Vy[m_R1(x,у)Λ m_R2(y,z)] называется max-min композицией или max-min сверткой отношений R1,R2

Пример

Пусть

R1	Y1	Y2	Y3
X1	0,1	0,7	0,4
X2		0,5

R2	Z1	Z2	Z3	Z4
Y1	0,9			0,2
Y2	0,3	0,6		0,9
Y3	0,1		0,6	0,5

Тогда свертка будет иметь вид

R1○R2	Z1	Z2	Z3	Z4
X1	0,3	0,6	0,1	0,7
X2	0,9	0,5		0,5

При этом:

µ R1○R2(х1,z1)= [m_R1(x1,у1)Λm_R2(y2,z2)]v[m_R1(x1,у2)Λm_R2(y2,z1)]v

v[m_R1(x1,у3)Λ m_R2(y3,z1)] = (0,1Λ0,3)v(0,7Λ0,3)v(0,4Λ0,1)=0,1v0,3v0,1=0,3

µ R1○R2(х1,z2)=(0,1Λ0,0)v(0,7Λ0,6)v(0,4Λ1)=0,1v0,6v0,4=0,6

p	q	p→q

Нечеткая импликацияПусть р - “x есть A”, q-“y есть B”, тогда импликацией х в четкой логике назовем предложение: “Если p, то q”, которое ложно тогда и только тогда, когда р истинно, а q ложно. Такое отношение обозначается p→q и называется “р влечет за собой q” и имеет таблицу истинности следующего вида:

Нечеткая импликация имеет тот же смысл, только степень истинности может принимать любые значения от 0 до 1.

Будем считать, что заданы универсальные множества X и Y. Под способом определения нечеткой импликации “если А, то В”, где А и В – нечеткие множества на X и Y соответственно, будем понимать способ задания нечеткого отношения R на X*Y, соответствующее данному высказыванию. Такое отношение можно задавать по-разному, поэтому для математического представления нечеткой импликации предложено большое количество формул, ассоциируемых с фамилиями авторов. Например, Larsen- - m_R(x,у)= µ_A(x)*µ_B(y); Lukasiewicz -m_R(x,у)=min{1,1-µ_A(x)1+µ _B(y)}; Mamdan - -m_R(x,у)=min{µ_A(x),µ _B(y)}.

В общем случае преимущества у какой-либо формулы нет.

Нечеткие выводы

В обычной логике выводы делаются в следующей последовательности: предпосылка: у=у0, факт х=х0 и следствие: y0=f(x0). Аналогично проводятся и операции с нечеткими понятиями, используемыми в разных экспертных системах, имеющих в своей основе базу знаний, формируемую экспертами в виде совокупности нечетких правил, вида: П1: если х есть А1, тогда у есть В1

П2: если х есть А2, тогда у есть В2, где х – входная переменная, у – переменная вывода. Аi,Bi – нечеткие множества, определенные соответственно на Х и У. Механизм нечеткого вывода можно представить в виде аналогичном, приведенному для четкой логики. Предпосылка: П1: если х есть А1, тогда у есть В1

П2: если х есть А2, тогда у есть В2,

факт х=А и следствие: y=В.

Рассмотрим более детально нечеткие выводы. Знания эксперта А→В отражают нечеткое причинное отношение предпосылки заключения, поэтому его можно назвать нечетким отношением и обозначить через R (R=A→В). Отношение R можно рассмотреть как нечеткое подмножество прямого произведения Х*У полного множества предпочтений Х и заключений У. Т.о., процесс получения нечеткого результата вывода В’ с использованием данного наблюдения А’ и знания А→В можно представить в виде:

B’ = A’○R=A’○(А→В)

Операция логического вывода для нечетких знаний осуществляется за 4 этапа:

1 Этап: Введение нечеткости (фазификация). Функции принадлежности, определенные на входных переменных применяются к их фактическим значениям для определения степени истинности каждой предпосылки каждого правила.

2 Этап: Нечеткая импликация. Вычисленное значение истинности предпосылок для каждого правила применяется к заключениям каждого правила. Это приводит к 1-му нечеткому подмножеству, которое будет назначено каждой переменной вывода для каждого правила.

3 Этап: Композиция. Все нечеткие подмножества, назначенные каждой переменной вывода (во всех правилах) объединяются вместе, чтобы формировать одно нечеткое подмножество для каждой переменной вывода. При этом используются операции V и Λ (max и min).

4 Этап: приведение к четкости (дефазификация). Он используется когда необходимо преобразовать нечеткий набор выводов в четкое число.

Пример. Пусть некоторая система описывается нечеткими правилами:

П1: если х есть А, тогда w есть D

П2: если y есть B, тогда w есть E

П3: если z есть C, тогда w есть F

Где X,Y,Z -имена входных переменных, w- имя переменной вывода, A,B,C,D,E,F – заданные функции принадлежности.

Правило:

Где w0- центр тяжести

Рисунок 1.

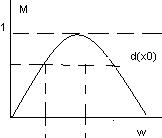
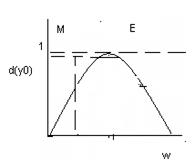
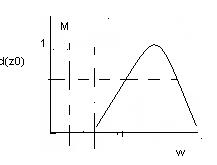
Процедура логического вывода показана на рисунке 1 предполагается, что входные переменные приняли некоторые логические знания x₀,y₀,z₀.

На первом этапе для данных x₀,y_0,z₀ исходя из функций принадлежности A.B,C находятся степенями истинности, для предпосылок каждого правила. На этапе два происходит “отсекание” функции принадлежности заключения правил D,E,F на уровнях α(x₀), α(y₀), α(z₀) соответственно.

На этапе три рассматриваются усеченные на втором этапе функции принадлежности и производится их объединение с использованием операции max-мум.

В результате получается комбинированное нечеткое подмножество с функцией принадлежности µ_∑, соответствующее логическому выводу для переменной w.

На четвертом этапе находится значение переменной w, например, с использованием цинтроидного метода четкое значение выходной переменной определяется, как центр тяжести для кривой µ_∑(w), то есть

W₀=(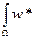 µ_∑(w)αw)/ ( µ_∑(w)αw)

Где

Ω- фигура ограниченности линий µ_∑ и осью w.

Рассмотрим модификации нечеткого вывода:

П1: если x есть A1 и y есть B1, тогда z есть С1

П1: если y есть А2 и y есть B2, тогда z есть С2

Где

X,Y-входные переменные

z- переменные выводы

A1,A2,B1,B2,C1,C2- некоторые заданные функции принадлежности.

Необходимо четкое значение Z₀ на основе четких значений x₀ и y₀.

Дата добавления: 2015-06-27