Уравнение Бернулли для стационарного течения несжимаемой жидкости

Для стационарного течения идеальной несжимаемой жидкости из основного уравнения динамики движения частицы вдоль трубки тока легко получить более простое и важное уравнение. В этом случае плотность и удельный вес жидкости остаются постоянными, и поэтому уравнение (101.5) может быть переписано так:

(102.1)

Обозначим через h высоту того места, где находится частица с ко­ординатой s; тогда смещение частицы на ds связано с изменением высоты на dh следующим образом (см. рис. 286):

(102.2)

поэтому заменим в (102.1) cosa на - dh/ds и получим

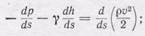(102.3)

здесь все члены представляют производные по координате s, сле­довательно,

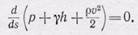(102.4)

Равенство нулю производной означает, что сумма трех величин остается постоянной вдоль трубки тока, или

(102.5)

Это и есть известное уравнение Бернулли для стацио­нарного течения несжимаемой жидкости. Оно играет фундаменталь­ную роль во всех гидродинамических исследованиях. В уравнении Бернулли р — «статическое» давление, давление, сжимающее ча­стицу жидкости; g h — изменение давления при изменении высоты

на величину h; rv ²/2 называется «динамическим давлением» (см. § 106).

При помощи уравнения Бернулли (102.5) просто решается много сложных задач. Действительно, если мы можем разбить поле текущей жидкости на трубки тока и определить по каким-то соображениям значения давления р ₀и скорости v ₀в какой-то точке, высота которой h ₀ нам известна, то, как бы ни изменялись по трубке и скорость, и давление, и высота, величина, вычислен­ная по формуле (102.5), останется неизменной. Это условие по­могает находить неизвестные величины в других местах течения. Как это делается, увидим при анализе различных примеров и задач.

Уравнение Бернулли представляет собой следствие закона сохранения энергии для частицы жидкости, движущейся вдоль трубки тока. Оно следует из того, что работа сил давления должна равняться увеличению суммы кинетической и потенциальной энергий частицы, ведь силы давления представляют внешние силы по отношению к рассматриваемой частице.

Рассмотрим изменение энергии и работу сил давления за время dt при перемещении частицы жидкости, которая в момент занимает участок трубки дли­ной ds (см. рис. 286). Пусть за это время задний (по потоку) фронт частицы переместился на отрезок ds ₁, который, вообще говоря, не равен длине частицы ds (на рисунке он показан более коротким). Тогда изменения, которые прои­зошли при перемещении частицы, сводятся к тому, что верхняя косо заштрихо­ванная часть объемом dQ=Sds ₁ перешла на место нижней косо заштрихован­ной части, имеющей тот же самый объем dQ;средняя, заштрихованная в клетку, часть не изменила своего состояния за время dt, хотя она через время dt состоит уже из других материальных частиц. Поэтому приращение (уменьшение) потен­циальной энергии частицы запишется в виде

(102.6)

если учтем равенство (102.2).

Приращение кинетической энергии равно

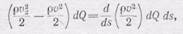(102.7)

где v ₂ — скорость на переднем фронте частицы длиной ds. Работа сил давле­ния при перемещении заднего фронта равна pSds ₁ =pdQ, при перемещении переднего фронта — (р + dp)dQ, и работа всех сил давления равна

(102.8)

Приравнивая работу сил давления изменению кинетической и потенциальной энергий частицы, получаем

(102.9)

Сокращая на dQds, получаем (102.4); интегрируя его вдоль линии тока, при­ходим к уравнению Бернулли (102.5).

Дата добавления: 2015-06-28