Давление в критической точке обтекаемого тела

Наиболее распространенным прибором, определяющим скорость потока, является трубка Пито; при помощи этой трубки измеря­ется и скорость движения тела относительно воздуха, например скорость самолета. В этом приборе используется связь между давлением в «критической» точке обтекаемого тела и скоростью потока.

Если в потоке жидкости и газа находится какое-то тело, ко­торое жидкость обтекает со всех сторон, то трубки тока как-то расходятся вдоль поверхности тела, примерно так, как показано на рис. 293. Поэтому на стороне тела, обращенной к потоку, есть такая точка А, называемая критической точкой, в которой трубки тока расходятся в различные стороны, охватывая тело. Так как поток в критической точке расходится, то очевидно, что скорость его в этой точке должна быть равна нулю и в силу непрерывности вблизи нее будет очень малой. Представим себе трубку тока, «упи­рающуюся», если можно так выразиться, в критическую точку; эта трубка заштрихована на рис. 293.

Тело находится в однородном потоке идеальной несжимаемой жидкости, поэтому на некотором достаточно удаленном расстоянии от тела всюду и давление р ₀,и плотностьr₀, и скорость v ₀

одинаковы; следовательно, константа Бернулли равна¹) р ₀+r₀ v ²₀/2

для всех трубок тока, или для всех точек потока. Так как в кри­тической точке скорость потока равна нулю, то, следовательно,

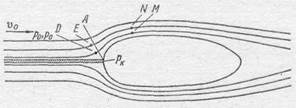
Рис. 293.

давление в этой точке р_к по уравнению Бернулли (102.5) равно

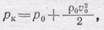(106.1)

или

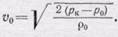(106.2)

Заметим, что давление в критической точке так же связано со ско­ростью потока вдали от тела, как и скорость и давление в сжатой жидкости, вытекающей из сосуда (см. (105.1)). Только картина по­тока в одном из этих случаев зеркально отображает другой.

Давление в критической точке тела, находящегося в потоке, которое в технике часто называют «давлением полного напора», можно измерить манометром. Обычно достаточно длинной трубкой соединяют отверстие, сделанное вблизи критической точки, ко­торую правильнее было бы называть критической областью, с ма­нометром. Давление в критической точке тела, находящегося в потоке, дает нам константу Бернулли для этого потока, назы­ваемую «полным напором». Зная полный напор, можно определить скорость потока в любой точке, если известно статическое давле­ние р ₀в потоке и плотность жидкости r₀.

Проще всего взять в качестве обтекаемого тела трубку, откры­тое отверстие которой направлено к потоку. Другой конец трубки соединен с манометром, измеряющим давление в трубке. Иногда вместо трубки берут цилиндрическое тело с закругленным концом

¹) В этой задаче полагаем, что членом g h можно пренебречь, ибо изменение высоты очень мало. Если нужно, то этот член всегда можно учесть.

(рис. 294), по оси которого сделано отверстие А, соединенное тру­бочкой с манометром. Этот цилиндр, укрепленный на соответствую­щей державке, направляют отверстием А к потоку так, что крити­ческая область лежит в зоне отверстия.

Для определения скорости потока v ₀,кроме полного напора р_к, нужно знать и статическое давление в потоке р ₀.Статическое давление в потоке определяют примерно так, как измеряют дав­ление в трубке с текущей жидкостью (см. рис. 291). Там в стенке

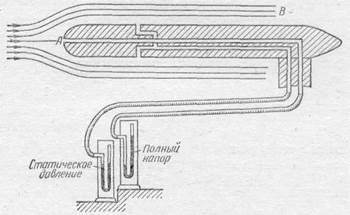
Рис. 294.

трубки делались отверстия, к которым и присоединялись маноме­трические трубки. Здесь для измерения давления в потоке уста­навливают цилиндрическое тело так, что его образующая направ­лена вдоль линий тока в невозмущенном потоке ¹),и измеряют дав­ление в некотором небольшом отверстии на стенке этого тела. Если сечение трубки тока, проходящей вблизи отверстия, будет таким же, как и сечение этой трубки вдали от тела, то давление у отверстия будет равно давлению вдали от тела ²). Отверстие посредством трубки соединяют с манометром, который и показы­вает статическое давление р ₀.

Отверстия для определения статического давления в потоке часто делают на поверхности того же цилиндрического тела, по­средством которого измеряется давление полного напора. В трубке Прандтля, сечение которой схематически показано на рис. 294, отверстия для измерения статического давления находятся на

¹)Это требование всегда выполняется, если ось цилиндра направлена по потоку и диаметр его ничтожно мал по сравнению с поперечными размерами струи потока.

²) Строго говоря, давление будет одинаково, если и температура в этих точ­ках одинакова.

некотором расстоянии от переднего конца цилиндра (примерно на расстоянии 3—5 диаметров), там, где трубки тока выравнива­ются. Эти отверстия посредством специальной резиновой трубки соединены с манометром, измеряющим статическое давление р ₀ в потоке.

Зная давление полного напора р_к и статическое давление р ₀, можно по уравнению (106.1) определить скорость набегающего потока.

Величину р _с=r₀ v ²₀/2 называют динамическим или «скоростным»

напором. Ее можно непосредственно измерить, если к манометру подвести с одной стороны полный напор р_к, а с другой — стати­ческое давление р ₀,тогда манометр покажет разность р _с,или ди­намический напор. По величине динамического напора опреде­ляют скорость.

Заметим, что для определения скорости воздуха приближенно можно пользоваться формулой

(106.3)

где скорость v измеряется в м/с, а разность давлений, или скорост­ной напор, р_с=h — в миллиметрах водяного столба. Эта формула следует из (106.2), если считать, как это принято в инженерной прак­тике, плотность воздуха

Для определения скорости сжимаемого газа (например, воз­духа) при значительной скорости ¹) необходимо уже учитывать изме­нение плотности и рассчитывать связь между давлением и ско­ростью в трубке тока так же, как это было сделано в § 105. Фор­мулами (105.5) и (105.7) можно пользоваться для вычисления скорости по давлению, если вместо р _нпоставить р_к — давление в критической точке. Но при очень большой скорости потока, близкой к скорости звука в газе, и эти соотношения неверны, так как при этих значениях скорости потока возникает новое явление — «скачок скорости и давления» перед телом, о котором будет сказано ниже, в § 120.

Дата добавления: 2015-06-28