Истечение жидкости или газа, находящихся под давлением в сосуде

Если жидкость или газ находятся в сосуде под давлением, много большим, чем давление, создаваемое весом жидкости, то изменениями давления по высоте столба жидкости можно прене­бречь и считать, что истечение подчиняется тем же законам, что и истечение жидкости, находящейся в замкнутом сосуде под давле­нием p _н.Поэтому можно просто определить скорость истечения воды из котла, в котором вода находится под постоянным давлением

пара в несколько десятков атмосфер, или скорость истечения газа из баллона (рис. 292), в котором давление поддерживается постоян­ным при помощи компрессора. В этих случаях можно считать кон­станту в уравнении Бернулли постоянной по всему объему теку­щего газа или жидкости и равной р _н,давлению в сосуде, так как скоростью течения в сосуде можно пренебречь вследствие того, что сечение сосуда S много больше сечения отвер­стия s.

Скорость истечения воды из котла будет равна

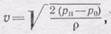(105.1)

как легко вычислить из урав­нения (102.5).

Для газа уже нельзя опре­делить скорость по формуле (102.5), ибо плотность газа r будет изменяться при движении ча­стицы газа к отверстию. Изменение давления вдоль трубки тока можно при стационарном течении записать по (101.5) так:

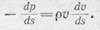(105.2)

Но плотность r теперь уже зависит от величины давления р. При подходе частиц к отверстию давление должно падать: ведь частицы ускоряются в направлении движения. И величина скорости будет зависеть от того, по какому закону изменяется плотность с изме­нением давления.

Вообще зависимость между давлением и плотностью довольно сложная, так как она связана еще и с изменением температуры вдоль трубки тока. Однако во многих случаях, когда частица движется достаточно быстро, можно считать, как показывает опыт, что дав­ление и плотность связаны законом адиабаты

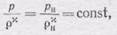(105.3)

где c— показатель адиабаты, зависящий от природы газа (для воздуха он равен 1,4), а r_н — плотность газа в сосуде. Закон адиабаты (105.3) следует из того, что во время расширения частицы не происходит обмена теплом с окружающими частицами.

Подставим зависимость плотности от давления в (105.2) и, преобразуя, получим

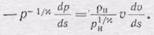(105.4)

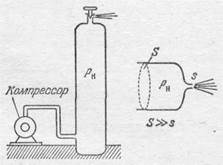
Рис. 292.

Это выражение можно проинтегрировать вдоль линии трубки тока. Если давление в баллоне р _н,а давление в пространстве, куда вытекает газ, равно р ₀,то интегрировать по давлению нужно от р _ндо р ₀, а по скорости — от нуля до v ₀— скорости на выходе:

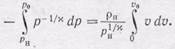
Выполняя интегрирование и преобразуя, получаем скорость исте­чения:

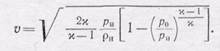(105.5)

Если бы мы полагали газ несжимаемым, то из (105.1) получили бы

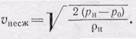(105.6)

Скорость истечения газа из баллона под давлением можно записать так:

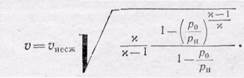(105.7)

Теперь легко оценить ошибку, какую допускают при расчетах, в которых газ полагают несжимаемым; для этого нужно только оценить величину корня в (105.7) при данной разности давлений. Можно убедиться непосредственным расчетом, что при очень ма­ленькой разнице в давлениях р _ни р ₀,равной, например, нескольким процентам, величина корня будет очень мало отличаться от еди­ницы. Тогда можно рассчитывать скорость и течение газа, как для несжимаемой жидкости.

Определим точнее величину ошибки, которую мы делаем, принимая воздух несжимаемым при давлении, близком к атмосферному. Допустим, что разность давлений в сосуде и вне его составляет 10% от атмосферного, и положим, что дав­ление в сосуде р _н равно 1 атм, а вне его р ₀=0,9 атм. Какова была бы скорость истечения, если бы воздух был несжимаемой жидкостью? Подставляя в (105.6) значение плотности воздуха

и величину атмосферного давления

,

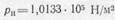получим

Вычислим теперь значение радикала в (105.7). Обозначим и

(c-1)/c =а, тогда радикал будет иметь такой вид:

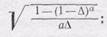
разлагаем (1-D) ^а в ряд Тейлора около единицы и получаем

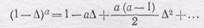
Подставляя это выражение в радикал и преобразуя, получаем

Подставляя сюда D=0,1 и c=1,4, находим, что ошибка в определении ско­рости составляет примерно 2%. Следовательно, в тех случаях, когда не нужно высокой точности при определении скорости при разностях давлений, меньших 10% атмосферного, можно пренебречь сжимаемостью воздуха и считать течение воздуха течением несжимаемой жидкости.

Очевидно, что при такой малой разности давлений вдоль трубки тока плот­ность будет изменяться так же мало; процентное отношение изменений давления и плотности будет примерно тем же. Действительно, при адиабатическом расши­рении газа на незначительную величину относительное изменение давления будет в c раз больше относительного изменения плотности: ведь из (105.3) получаем dp/p =c d r/r. Небольшое изменение плотности вдоль трубки тока не оказывает влияния на величину скорости, а следовательно, и на характер течения.

Дата добавления: 2015-06-28