Сила реакции текущей воды

Применим закон изменения количества движения для опре­деления реакции протекающей жидкости на трубу, по которой она течет. Всякий наблюдал, как резко разворачивается гибкий шланг для поливки улиц, когда в изогнутый шланг пускают струю воды. Изогнутый шланг должен был бы изменить направление количества движения воды (рис. 298), но силы, приложенные к объему теку­щей воды со стороны изогнутого шланга, очень малы, поэтому шланг выпрямляется, так что количество движения выходящей жид­кости совпадает по направлению с количеством движения входящей.

Определим реакцию воды на кран, показанный на рис. 299. Выделим объем жидкости так, как указано на рис. 299 пунктиром; поверхность его совпадает с внутренней поверхностью крана и двумя его поперечными сечениями А и В. Поперечное сечение трубы

крана не меняется, поэтому и скорость v в каждом сечении одина­кова по абсолютной величине. Тогда количество движения жидко­сти, ежесекундно входящей в дан­ный объем, равно

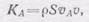(110.1)

где, как обычно, r — плотность воды, v _A — скорость и S — пло­щадь поперечного сечения крана. Вектор количества движения К _A направлен перпендикулярно к се­чению А. Количество движения ежесекундно выходящей из вы­деленного объема жидкости К _B численно равно модулю К _A, но направлено к нему под углом 90°. Поэтому вектор изменения количества движения направлен так, как показано на рис. 299, и равен в данном случае силе

(110.2)

а величина его

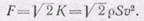
Теперь рассмотрим силы, действующие на выделенный объем. Действием силы тяготения можно пренебречь ¹), поэтому остаются только силы давления по поверхности выделенного объема. Рас­смотрим их последовательно. Силы давления в сечениях входа А и выхода В жидкости одинаковы, если пренебрежем вязкостью воды. В самом деле, из уравнения Бернулли следует, что вдоль трубки тока при одинаковых скоростях будут и одинаковые дав­ления. Давление на выходе струи равно атмосферному. Силы атмосферного давления на входе и выходе струи уравновеши­ваются давлением на кран извне, и поэтому их результирующая сила на кран равна нулю, так же как атмосферное давление на пустой кран не дает результирующей, если пренебречь подъемной силой воздуха.

Остается только действие сил давления крана на воду по ос­тальной части поверхности выделенного объема. Сумма этих сил, или результирующая сила давления крана на вытекающую жид­кость, равна F — ежесекундному изменению количества движения, величину и направление которого мы знаем из (110.2). Поэтому реакция вытекающей жидкости на кран равна и противоположна

¹)Эта сила тяжести жидкости, находящейся в объеме, практически очень мала по сравнению с искомой силой. Очевидно, что учет этой силы не представ­ляет особого труда.

Рис. 298.

вектору изменения количества движения F, она проходит через точку О (см. рис. 299), точку пересечения линий направления количества движения входящей и выходящей жидкости.

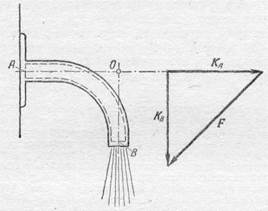
Рис. 299.

Определим силу действия на сосуд струи жидкости, вытека­ющей из него (рис. 300). По уравнению Бернулли (102.5) скорость истечения равна

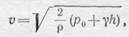(110.3)

где р ₀— давление над жидкостью в сосуде ¹), h — высота уровня над отверстием. Выделим объем жидкости, как показано на рис. 300. Ради простоты вычис­лений положим, что сосуд имеет прямоугольное горизонтальное сечение, и потому рассмотрим силы давления и изменения ко­личества движения жидкости только на поверхностях, нор­мальных к струе; во всех осталь­ных направлениях изменение ко­личества движения жидкости равно нулю. Поэтому будем рассчитывать и силы и приращение количества движения в направлении скорости струи.

Если поперечное сечение струи S ₀, то изменение количества движения за секунду по направлению струи равно

(110.4)

¹) Точнее, р ₀ — величина, на которую давление в сосуде превышает атмо­сферное.

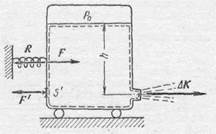
Рис. 300.

где Q — массовый ежесекундный расход. Сосуд действует на жид­кость с силой F =D K, а реакция R жидкости на сосуд равна ве­личине F и противоположно направлена. Силу R называют реак­тивной силой, она в точности равна реактивной силе, определенной по формуле Мещерского (§ 27).

Реактивную силу вытекающей струи можно определить опыт­ным путем, если измерить силу, действующую на сосуд, при по­мощи динамометра, как это схематически показано на рис. 300. Примерно таким же способом измеряют силу тяги реактивных двигателей и ракет.

Интересно проследить, как реактивная сила передается на стенки сосуда. Реактивная сила создается вследствие разности давлений на стенки сосуда, разности, возникающей при вытекании струи. Давление на задней стенке (рис. 300) можно считать равным р ₀плюс гидростатическое давление g h (g — удельный вес жидкости, а h — глубина точки), ибо скорость течения у этой стенки очень мала, ничтожно мала по сравнению со скоростью в струе вытекающей жидкости. Давление на передней стенке сосуда (см. рис. 300), на той стенке, в которой на­ходится отверстие, не будет равным давлению на задней стенке. Если бы это было не так и давления на передней и задней стенках были бы одинаковы, то они урав­новешивались бы во всех противолежащих площадках, за исключением площадки S' = S ₀,расположенной на задней стенке против отверстия площадью S ₀.Поэто­му общая сила давления жидкости на заднюю стенку, как и следовало ожидать, будет больше. Определим величину силы давления на площадку S', полагая размеры ее очень малыми по сравнению с h. Эта сила F ', очевидно, будет равна

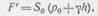(110.5)

Учтем формулу (110.3) и запишем:

сравнивая это с (110.4), видим, что сила F' ровно в два раза меньше реактивной силы R. Поэтому считать давление на противоположных стенках сосуда одина­ковым неправильно, т. е. нельзя пренебрегать скоростью течения у передней стенки вблизи отверстия, вследствие которой давление в этой области будет пони­жено. Для точного определения изменений распределения давления на стенки сосуда нам нужно было бы рассчитать все течение в сосуде, что представляет очень сложную задачу, а по закону изменения количества движения задача об определении силы реакции решается просто без такого расчета.

Из этих рассуждений видно, что падение давления у передней стенки вблизи отверстия дает силу, равную половине реактивной силы R. Заметим, что этот вывод справедлив только тогда, когда наименьшее сечение струи S ₀равно пло­щади отверстия, а это не всегда имеет место.

До сих пор мы предполагали, что струя выходит из «насадка» с довольно плавными переходами от вертикальной стенки, в этом случае струя выходит из отверстия параллельными трубками тока, заполняя все отверстие примерно так, как показано на рис. 301, а. Если не сделать плавных переходов к «насадку» от стенок, то струя будет сжиматься (рис. 301, б). Такое сжатие струи легко объяс­нить. Крайние струйки жидкости, подходящие к отверстию вдоль стенки, далее вследствие своей инерции стремятся к центру струи, и только под давлением частиц, идущих ближе к центру струи, крайние линии тока выпрямляются. В этом случае минимальное сечение струи, сечение в том месте, где трубки тока практически выпрямляются, меньше сечения отверстия. Величина отношения площади минимального сечения струи к площади отверстия зависит от формы краев отверстия и определяется опытным путем.

В случае острого края отверстия площадь сечения струи много меньше пло­щади отверстия, но больше половины этой площади. Если струя выходит из трубочки с острыми краями, направленной внутрь сосуда (рис. 301, в),то пло­щадь минимального сечения струи в точности равна половине площади отверстия.

Рис. 301.

Здесь скоростью течения вдоль вертикальной стенки сосуда, в которую вделана трубка, можно вполне пренебречь, так как вертикальная стенка сосуда удалена от отверстия. Тогда давление на противоположных участках стенок сосуда одина­ково и сила реакции по (110.5) должна быть равна

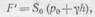(110.6)

где S ₀ — площадь отверстия трубки. А из закона изменения количества движения сила реакции должна быть равна

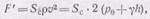(110.7)

где S _c — площадь поперечного сечения струи в самом узком месте (рис. 301, в). Сравнивая (110.6) и (110.7), заключаем, что

(110.8)

или сужение струи (отношение площади струи к площади отверстия) равно ¹/₂. Это соотношение хорошо подтверждается опытами.

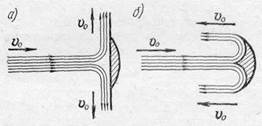
Рис. 302.

Применение закона изменения количества движения особенно полезно там, где легко определить направление и скорость струи. Например, при паде­нии струи на лопатку колеса турбины с желобками такого вида, как показано на рис. 302, б, сила давления будет в два раза больше, чем при падении струи

такой же скорости и сечения на плоскую лопатку, показанную на рис. 302, а. Конечно, при таких условиях приближенно можно считать, что скорость струи при ударе о лопатку с желобками остается неизменной по величине, и скорости движения лопаток и в том и в другом случае одинаковы и достаточно малы по сравнению со скоростью движения частиц в струе.

Дата добавления: 2015-06-28