Распределение давления во вращающейся жидкости

Размешивая чай в стакане, можно наблюдать поверхность вращающейся жидкости — она принимает параболическую форму. Представим себе стакан или другой цилиндрический сосуд на диске центробежной машины (рис. 296).

Если диск вращается с угловой скоростью со, то через некото­рое время все частицы жидкости будут двигаться по окружности так, что жидкость останется неподвижной относительно стенок стакана. Так как частицы по трубке тока движутся по кругу ра­диуса r, то давление в горизонтальной плоскости будет возрастать по мере удаления от оси вращения. Градиент давления вдоль ра­диуса r по (107.3) будет равен ¹)

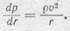(108.1)

Заменим в (108.1) окружную скорость частицы v через w r и получим

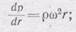(108.2)

это уравнение можно проинтегрировать по r:

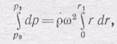
или

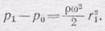(108.3)

¹) Так как движение стационарное, то давление р в горизонтальной пло­скости можно считать функцией только от r.

Отсюда видно, что давление в горизонтальном сечении сосуда возрастает пропорционально квадрату расстояния от оси враще­ния. Как известно, давление в каждой точке жидкости должно быть одинаково по всем направлениям, поэтому и уровень жид­кости должен повышаться с расстоянием от оси. Действительно, изменение давления в вертикальном направлении возникает только за счет веса жидкости; поэтому для того, чтобы частица жидкости покоилась относительно стакана, необходимо, чтобы уровень жид­кости над кольцевой пло­щадкой радиуса r ₁был выше уровня жидкости в центре на величину h. Давление, создаваемое весом жидкости на го­ризонтали, проходящей через нижнюю точку свободной поверхности (точку О на рис. 296), равно hg, и оно дол­жно равняться давлению

rw² r ²₁/2 где r ₁ — расстоя­ние рассматриваемой точки до оси. Поэтому

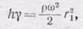
или

так как g=r g, где g — ускорение силы тяго­тения. Высота уровня жидкости растет пропорционально квадрату расстояния от оси вращения, т. е. свободная поверхность предста­вляет собой параболоид вращения, как и наблюдается в опытах.

Форма свободной поверхности показывает изменение давления вдоль радиуса. Но можно это проверить еще и таким образом: бросить в стакан с водой, вращающийся на центробежной машине, небольшие кусочки вещества тяжелее воды, все они через некоторое время расположатся внизу у стенки стакана. Кусочки вещества, плавающего на поверхности воды, будут собираться вблизи точки О.

Интересно проследить, как будут вести себя в стакане кусочек свинца и шарик воска, связанные ниткой, (воск легче воды). По­пробуйте в качестве упражнения сами проанализировать резуль­тат такого опыта. Каково будет распределение давления во вращаю-

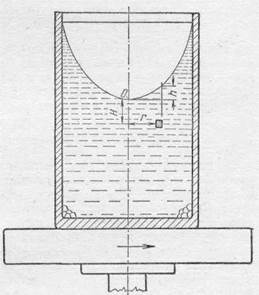
Рис. 296.

щемся сосуде, если он закрыт со всех сторон? Каковы будут распре­деление давления и форма поверхности, если центр стакана с водой расположен не на оси машины?

Отметим, что в рассмотренном случае движения частиц жид­кости при вращении сосуда постоянная Бернулли сохраняет свою величину только для одной трубки тока и различна для разных линий тока. Вспоминая (102.5) и учитывая (108.3), можно записать для трубки тока

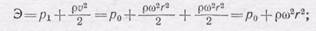
так как трубки тока горизонтальны, то член, в который входит h, можно не принимать во внимание. Величина р ₀ — давление на оси — зависит только от глубины и равна g Н (см. рис. 296). Сле­довательно, постоянная Бернулли (Э) изменяется и с глубиной, и с расстоянием от оси вращения.

Дата добавления: 2015-06-28