Течение вязкой жидкости в трубе

Во многих случаях допустимо пренебречь силами вязкости и приближенно анализировать явление так, как если бы силы вяз­кости отсутствовали. Это желательно делать не только потому, что еще не известны общие методы анализа течения при учете сил вязкости, но главным образом потому, что в ряде практически важных примеров результаты опытов с обычной жидкостью в пределах известной точности согласуются с результатами теоре­тического анализа течения «идеальной» жидкости. Важно только знать, когда пренебрежение вязкостью не ведет кпринципиальным и большим ошибкам.

Как известно, силы вязкости пропорциональны изменению скорости потока в направлении, перпендикулярном к скорости, и, следовательно, они будут сказываться особенно резко там, где эти изменения скорости велики. При обтекании вязкой жид­костью твердых тел частицы жидкости, непосредственно приле­гающие к телу, как бы «прилипают» к нему и имеют нулевую ско­рость относительно тела. Поэтому в непосредственной близости от поверхности твердого тела скорость потока нарастает от нулевого значения до некоторой величины. Дальше от тела изменения ско­рости потока сравнительно малы, и там совершенно ничтожно влияние вязкости.

Слой окружающей тело жидкости, в котором нарастает скорость и в котором влияние вязкости существенно, называется погранич­ным слоем. В некоторых случаях этот слой очень тонок и влиянием его можно пренебречь: течение вязкой жидкости или газа близко к тому течению, которое имело бы место при обтекании этого тела идеальной жидкостью, лишенной вязкости. В других случаях погра­ничный слой не будет тонким, и тогда уже нельзя пренебрегать вяз­костью. Так, например, при течении' вязкой жидкости в узкой трубе такой слой может заполнить весь объем текущей жидкостью, и при анализе этого течения необходимо учитывать силы вязкости.

Произведем опыты с измерением распределения давления мано­метрическими трубками в жидкости, текущей по горизонтальной трубе постоянного сечения (рис. 303). Если жидкость достаточно вязкая, например глицерин или какой-нибудь сироп, или труба достаточно тонкая, то давление будет падать равномерно вдоль трубы. Это можно видеть по тому, что уровни во всех равноотстоя­щих друг от друга манометрических трубках лежат на наклон­ной прямой (см. рис. 303). Если.бы жидкость была невязкой, то

уровни во всех трубках были бы одинаковы, давление вдоль трубки было бы постоянным.

Действительно, жидкость можно считать вполне несжимаемой, поэтому скорость течения в каждом сечении трубки одинакова, — ведь трубка имеет постоянное сечение, а по уравнению Бернулли и давление должно было быть одинаковым. В данном случае в вязкой жидкости на частицу, кроме сил давления, действуют еще и силы вязкости, поэтому при стационарном течении с постоянной скоростью давление падает вдоль трубки тока.

Течение происходит вдоль трубы прямолинейно, скорости всех частиц направлены вдоль оси трубы, следовательно, силы вяз-

Рис. 303.

кости будут действовать только в направлении оси трубы. Падение давления вдоль трубки тока уравновешивается силами вязкости, и поэтому скорость течения жидкости остается постоянной вдоль трубки.

Рассмотрим подробнее стационарное течение вязкой жидкости в прямой горизонтальной трубе постоянного сечения. Давление в каждом поперечном сечении можно считать одинаковым. Если этого не было бы, то линии тока изгибались бы или возникали бы течения поперек трубы. Все частицы жидкости, прилегающие к стенке круглой трубы, прилипли к ней и имеют скорость, равную нулю, кольцевой слой, прилегающий к ним, из условия симметрии должен иметь по всей окружности одинаковую скорость. Если представим себе жидкость разделенной на достаточно тонкие концентрические кольцевые слои, то скорость в каждом таком слое одинакова; поэтому величину скорости течения можно полагать только функцией расстояния r данной частицы от оси трубы.

Выделим из объема текущей жидкости цилиндр радиуса r, длиной dl (рис. 304) и напишем условия движения цилиндра.

Жидкость движется равномерно, следовательно, сумма всех сил, приложенных к выделенному цилиндру, равна нулю. Разность сил давлений на концах цилиндра

должна быть уравновешена силами вязкости, приложенными на поверхности цилиндра. Сумма сил вязкости равна площади боковой поверхности цилиндра 2 prdl, умноженной на напряжение сил

вязкости t. Равенство нулю всех внешних сил, действую­щих на цилиндр, теперь можно записать так:

или

(111.1)

По закону Ньютона (см. (39.1)) напряжение сил вязкости

пропорционально производной от скорости в перпендикулярном

направлении, в направлении радиуса,

(111.2)

где m — коэффициент вязкости жидкости и знак минус стоит потому, что скорость убывает с увеличением радиуса. Подставляя (111.2) в равенство (111.1), получаем

(111.3)

Величина градиента давления вдоль оси трубы dp/dl не зависит от радиуса, так как давление р в любом поперечном сечении одина­ково. Поэтому из уравнения (111.3) можно найти зависимость ско­рости течения от радиуса, проинтегрировав это уравнение по радиусу, учитывая при этом, что у стенки скорость v (R)=0,

(111.4)

где R — радиус трубы. После вычислений получаем

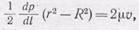
или

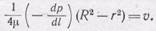(111.5)

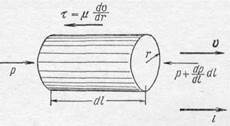
Рис. 304.

Давление равномерно падает в направлении скорости, и поэтому величина — dp/dl положительна и постоянна. Скорость будет макси­мальна на оси трубы, и распределение вели­чины скорости по диаметру трубы происхо­дит по параболическому закону (рис. 305). Максимальная скорость равна

Распределение скоростей течения вязкой жид­кости в трубе можно наблюдать по движению границы раздела двух различно окрашенных жидкостей. В вертикальной трубке налит окрашен­ный сахарный сироп (рис. 306, а), а сверху нужно аккуратно налить тот же сироп, но без краски. В состоянии покоя граница раздела горизонтальна. После открытия крана внизу трубки начинается медленное движение вязкой жидкости, и граница раздела начинает изменять с течением времени свою форму, все вытягиваясь по оси (см. рис. 306, а).

Зная распределение скорости, можно подсчитать объемный расход жид­кости Q через поперечное сечение трубы. Через кольцо радиуса r и площадью

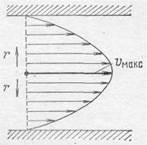
Рис. 305.

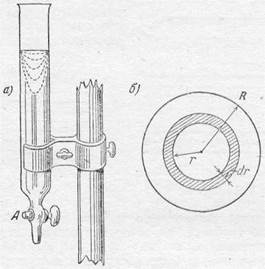
Рис. 306.

2 prdr за секунду пройдет объем жидкости dQ=v 2 prdr (рис. 306, б), а через все сечение

(111.6)

Здесь мы приняли во внимание формулу (111.5).

Пользуясь этим законом, можно построить простой прибор для измерения коэффициента вязкости mжидкости, схема которого дана на рис. 303. Величину dp/dl можно вычислить на основании результатов измерения давления в раз­личных точках трубы. Так как давление падает пропорционально длине, то

(111.7)

где р _н — давление в начале, а р _к — в конце отрезка трубы длиной l.

Величину расхода Q можно измерить непосредственно, измерив количество жидкости, прошедшей за определенное время через трубу. Зная радиус трубы R, можно на основании этих данных определить коэффициент вязкости mжидкости.

Течение жидкости в цилиндрической трубе, при котором ско­рости частиц всюду направлены вдоль оси, называется ламинар­ным или слоистым. Такое течение наблюдается при небольшом

значении скорости потока вязкой жидкости. С увеличением ско­рости потока, с увеличением перепада давления на концах трубы, течение принципиально изменяет свой характер: вместо спокойного слоистого течения наблюдается турбулентное, или завихренное, течение.

Рис. 307.

Рис. 308.

Возникновение завихренного течения легко наблюдать, если в стеклянную трубочку, по которой протекает вода из сосуда, пустить подкрашенную струйку (рис. 307, а).При небольшой скорости потока течение будет слоистым и подкрашенная струйка в виде почти прямой линии будет идти параллельно оси трубки (рис. 307, б). Затем, при постепенном увеличении скорости потока, внезапно начинается завихренное движение и струйка размывается в широкую ленту с неровными краями, как показано на рис. 307, в.

При стационарном турбулентном движении скорость в данном месте не остается постоянной по величине и направлению, а совер­шает быстрые беспорядочные колебания как по величине, так и по направлению. Но среднее значение скорости будет постоянной

определенной величиной, направленной вдоль оси трубки. Поэтому в завихренном потоке чаще всего определяют среднее значение скорости.

Чем определяется возникновение турбулентности, мы скажем ниже, в § 113, а здесь отметим, что распределение средней скорости при турбулентном потоке по диаметру трубы совсем иное (рис. 308), отличное от того, что мы видели при ламинарном движении (см. рис. 305). При завихренном движении средняя скорость почти по всему сечению трубы остается почти постоянной и только вблизи стенок быстро спадает до нуля; пограничный слой вблизи стенок занимает сравнительно небольшую долю потока, а' в центре поле скоростей почти однородно и более похоже на то, которое должно быть в трубе при отсутствии вязкости жидкости. При слоистом движении (см. рис. 305) нет четкого пограничного слоя, во всех частях трубы поле скоростей изменяется из-за сил вязкости так же, как вблизи стенок; можно даже сказать, что в этом случае погра­ничный слой занимает весь поток жидкости.

Дата добавления: 2015-06-28