Истечение жидкости из сосуда

Пользуясь уравнением Бернулли (102.5), легко определить скорость весомой жидкости, вытекающей из сосуда. Пусть жид­кость вытекает из сосуда, имеющего сбоку отверстие (рис. 288). Отверстие снабжено специальным «насадком», который направ­ляет струю. При истечении вся жидкость в сосуде придет в движе­ние, и ее можно разбить на трубки тока. Точное разбиение жидко­сти на трубки тока представляет довольно сложную задачу даже

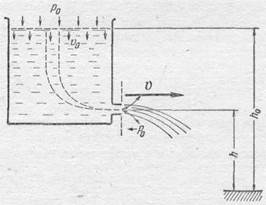
Рис. 288.

при простой форме сосуда. Но нам нет необходимости знать, как идут трубки тока по всему объему текущей в сосуде жидкости, нам достаточно знать, что все трубки тока начинаются на свободной поверхности жидкости и обязательно проходят через отверстие «насадка».

На свободной поверхности жидкости все трубки тока имеют одинаковую скорость v ₀,одинаковое давление р ₀и одинаковую высоту h ₀, так как поверхность жидкости при истечении опускается вниз, оставаясь горизонтальной, если она значительно выше уровня отверстия. Следовательно, постоянная в уравнении Бернулли (102.5) имеет одинаковую величину для всех трубок тока, равную

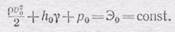(103.1)

Заметим, что так будет всегда, когда течение всех частиц иде­альной жидкости начинается из одинакового состояния, и тогда постоянная уравнения Бернулли имеет одинаковое значение не только для данной трубки тока, как мы вывели ранее, а для всего пространства текущей жидкости, занятого частицами, вытекаю­щими при одинаковых условиях. Это еще более упрощает анализ течения.

Так как диаметр отверстия мал по сравнению с высотой жид­кости в сосуде, то будем считать давление во всем поперечном сечении струи одинаковым и равным окружающему давлению р ₀. Также и скорость течения в струе для всех трубок тока можно считать одинаковой и равной v. Следовательно, по уравнению Бернулли (102.5)

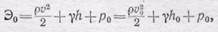(103.2)

или

(103.3)

где h — высота отверстия, a h ₀ — высота свободной поверхности в сосуде.

Если площадь отверстия составляет ничтожную долю от пло­щади поперечного сечения сосуда, то скорость v ₀будет ничтожно мала по сравнению со скоростью v и членом с v ²₀ в формуле (103.3) можно пренебречь. Поэтому скорость вытекающей жидкости равна

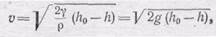(103.4)

так как g/r= g — ускорению силы тяжести.

Это так называемая формула Торричелли. Скорость истечения весомой жидкости из отверстия в сосуде равна той скорости, которую получит тело, падая с высоты, равной разности высот отверстия и свободной поверхности h ₀- h. Отметим, что величина скорости совершенно не зависит от направления к горизонту вы­текающей струи. Она будет одинакова, под каким бы углом струя ни вытекала. Поэтому, если направить струю вертикально вверх, то частицы жидкости, как и всякое тело, должны подняться на высоту уровня свободной поверхности жидкости¹). Однако из-за трения в жидкости, а главным образом из-за трения о частицы жидкости, падающие вниз, и трения в воздухе струя не достигнет

¹) Силы трения (вязкости) при течении воды по резиновой трубке, соединяю­щей «насадок», из которого вытекает струя, с сосудом, не окажут значительного влияния, если диаметр трубки будет велик по сравнению с диаметром выте­кающей струи.

уровня жидкости в сосуде (рис. 289, а). Но если направить струю под небольшим углом к вертикали (рис. 289, б), то она поднимется почти до уровня поверхности жидкости.

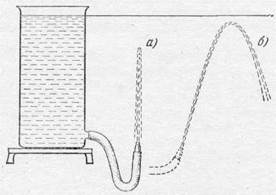
Рис. 289.

Справедливость формулы Торричелли можно проверить раз­личными способами. Например, можно наблюдать точку пересе­чения двух струй, вытекающих в горизонтальном направлении из

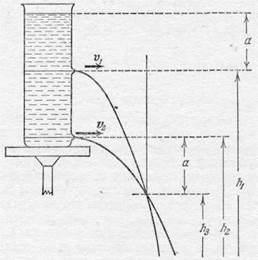
Рис. 290.

отверстий, находящихся на разной высоте (рис. 290). Если пре­небречь вязкостью, то легко показать расчетом, что струи пере­секутся на некоторой горизонтали, лежащей ниже нижнего от-

верстия на некотором расстоянии, равном расстоянию между уровнем жидкости в сосуде и верхним отверстием. Опыт под­тверждает это. Особенно наглядны изменения точки пересечения струй при подливании в сосуд значительного количества воды, при котором уровень воды меняется.

Расчет прост. Если скорость вытекающей жидкости определяется по закону Торричелли, то

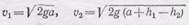
(смысл обозначений можно видеть на рис. 290). Время падения частицы до точки пересечения в каждой струе определяется по формулам

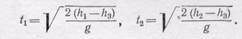
В точке пересечения струй удаление от сосуда обеих струй одинаково. При па­дении частиц горизонтальная компонента скорости не меняется, следовательно, v ₁ t ₁= v ₂ t ₂;отсюда

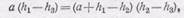
или

Дата добавления: 2015-06-28