Стационарное течение жидкости

ТЕЧЕНИЕ ЖИДКИХ И ГАЗООБРАЗНЫХ ТЕЛ

При движении жидкости и газа между отдельными частицами возникают силы внутреннего трения, или силы вязкости. Коэф­фициент вязкости таких веществ, как, например, воздух, вода, относительно невелик, поэтому при определенных условиях (при каких — это выясним подробнее далее) можно приближенно рас­сматривать течение жидкости (или газа) как течение «идеальной» жидкости, т. е. жидкости, лишенной вязкости. Такой жидкости и такого газа, разумеется, нет. Однако течение жидкости и газа во многих практически очень важных случаях можно прибли­женно рассматривать как течение идеальной жидкости.

Зная законы течения идеальной жидкости, можно уже в них внести поправки, учитывающие влияние вязкости. Такой путь последовательного изучения закономерностей движения жидкости и газа позволяет относительно простыми способами выяснить слож­ные законы движения вязкой жидкости.

Картину текущей жидкости (газа) можно представить себе при помощи поля вектора скоростей частиц. Каждой точке пространства r соответствует в момент времени t вектор v ( r, t) — вектор ско­рости частицы, проходящей через точку r, он зависит от положения точки r и времени t.

Течение жидкости (или газа) называют стационарным, если все величины: скорость, давление, плотность, температура и т. д. — остаются постоянными все время в каждом месте пространства, занятого текущей жидкостью. В противном случае движение назы­вается неустановившимся (или нестационарным), и законы течения будут еще сложнее.

Стационарное течение газа по трубам или стационарное течение воды по трубам, каналам и рекам представляет довольно сложную картину, даже и с кинематической точки зрения. Вообще говоря, во всех точках пространства, занятого движущейся жидкостью, скорости частиц различны по величине и по направлению. Дав-

ление, под которым находятся движущиеся частицы, также раз­лично, хотя оно закономерно связано с движением частиц. В дви­жущемся газе меняется от места к месту его плотность, поскольку изменяется давление и изменяется температура и т. д.

Рис. 282.

Анализ картины стационарного течения значительно упростится, если мы разобьем текущую жидкость ¹) на достаточно тонкие трубки тока. Представим себе в некотором месте жидкости твердое ко­лечко А из тончайшей нити (рис. 282), стоящее поперек потока; проведем траектории всех тех частиц, которые коснулись колечка с внешней стороны. Совокупность этих траекторий и образует трубку. Такую трубку можно продолжить вдоль по тече­нию, стенки ее образованы частицами, которые когда-то прошли вблизи нити кольца; и также вверх по течению ее стенки образованы теми части­цами, которые пройдут около нити колечка в свое время.

Жидкость непрерывна, следовательно, и стенку труб­ки можно мыслить как сплош­ную, непроницаемую. Ско­рость частиц на стенках труб­ки касательна к поверхности трубки. Можно все простран­ство текущей жидкости раз­бить на такие трубки тока. Для наблюдения картины течения некоторые трубки тока можно отметить, сделать видимыми. Так, например, в поток воздуха можно выпускать струйки дыма или какого-либо окрашенного газа, а в поток воды — в определенных местах краску, как это сделано в демонстрационном приборе для наблюдения картины обтекания тел, показанном на рис. 283. Частицы жидкости, прошедшие вблизи отверстия, из которого

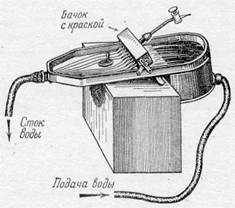
Рис. 283.

¹) Далее мы будем подразумевать под потоком жидкости и поток газа, не оговаривая это специально, за исключением тех случаев, когда различие между жидкостью и газом будет существенным.

выпущена краска (или дым), отмечают трубки тока в потоке, которые можно наблюдать глазом или фотографировать.

Очевидно, что стенки трубки тока в данном случае образованы траекториями частиц. Частица жидкости, находящаяся в какой-то трубке, так и будет в ней оставаться в течение всего времени дви­жения. Так как сечение трубки мы можем взять сколь угодно малым, то всегда можно считать, что скорость частиц жидкости одинакова в поперечном сечении трубки и направлена перпендику­лярно к нормальному сечению трубки.

Течение в трубке тока будет таким же, как и течение без тре­ния в трубке с жесткими стенками, сечение которой достаточно плавно изменяется.

. При неустановившемся течении можно представить себе трубки тока, но они уже не будут образованы траекториями частиц. Дей­ствительно, представим векторное поле скоростей v ( r, t) частиц в момент времени t. В этом поле можно мысленно провести линии тока — такие кривые, касательная к которым всюду совпадает по направлению с вектором скорости v. Эти кривые, проходящие через «колечко», образуют трубку тока. Ясно, что трубка тока, образованная линиями, проходящими через данное «колечко», зависит от времени. Кроме того, следует отметить, что линия тока, вообще говоря, совсем не совпадает с траекторией частицы, потому что, когда частица перейдет в соседнюю точку r + d r, вектор ско­рости в этой точке за время dt уже изменится на какую-то величину, и т. д. А при построении линий тока принимаются во внимание только скорости в данный момент во всех точках пространства. Ли­нии тока образованы смещениями различных частиц, а траектория — движением одной частицы.

Рассмотрим условие постоянства потока массы при течении по трубке. При стационарном течении масса жидкости или газа, прошедшая за единицу времени через любое поперечное сечение трубки, одинакова для всех сечений.

Представим себе трубку с площадью сечения S. Скорость в этом сечении равна v;тогда масса жидкости, прошедшая за секунду через это сечение, равна

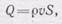(100.1)

где r — плотность жидкости или газа в данном сечении. Тогда в другом сечении трубки площадью S ₁ количество (масса) жидкости, прошедшей за секунду, должно быть также равно

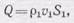(100.2)

где v ₁и r₁ — скорость и плотность жидкости во втором сечении трубки. В противном случае количество жидкости между этими двумя сечениями начало бы возрастать и убывать и течение пере¹-стало бы быть стационарным.

Следовательно, закон постоянства потока массы может быть записан так:

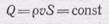(100.3)

вдоль любой трубки тока.

Если жидкость несжимаема, какой является, например, при обычных опытах вода, то плотность жидкости r остается посто­янной, и поэтому на основании закона постоянства потока массы (100.3) скорость в любом сечении трубки обратно пропорциональна

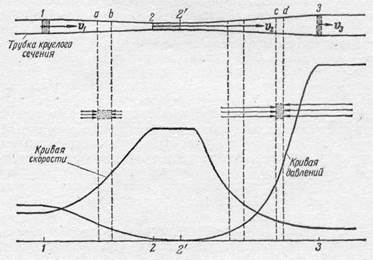
Рис. 284.

площади поперечного сечения. Таким образом, форма трубки опре­деляет и скорость течения: скорость возрастает там, где трубки тока сужаются, и, наоборот, падает там, где они расширяются (рис. 284).

Такая же картина будет и при течении по широкой трубе, у ко­торой сечение довольно плавно изменяется, так что на расстоя­нии, примерно равном длине диаметра трубы, ее можно считать с достаточной степенью точности цилиндрической. Если плотность газа или жидкости в такой трубе не изменяется, то при стационар­ном течении скорость в каждом поперечном сечении обратно про­порциональна площади этого сечения.

Найдем связь между изменением скорости и изменением дав­ления вдоль трубки тока. Проследим частицу жидкости, занимаю­щую некоторый отрезок трубки тока (см. рис. 284). Можно пред­ставлять себе течение так, что эта частица движется вдоль трубки, деформируясь и занимая все сечение трубки.

Что можно сказать о давлении вдоль трубки тока, если мы бу­дем следить за движением частицы? Совершенно очевидно, что если поперечное сечение трубки тока на данном участке постоянно, то и скорость частицы несжимаемой жидкости остается постоянной. Следовательно, частица на этом участке не имеет ускорения. Если трубка сужается вдоль потока (участок 1 — 2), то частица жидкости здесь ускоряется, скорость ее возрастает. Если же трубка расши­ряется (участок 2'— 3), то частица жидкости замедляется, скорость ее падает на этом участке.

Какие силы сообщают частице ускорение, если трубка гори­зонтальна? Только силы давления со стороны соседних частиц; следовательно, в сужающейся трубке тока (участок 1 — 2) давле­ние должно падать в направлении течения, т. е. давление сзади частицы (ab)должно быть больше, чем спереди, чтобы сообщить частице ускорение и обеспечить нарастание скорости. В расши­ряющейся трубке (участок 2'— 3),где скорость частицы умень­шается по течению, давление возрастает, частица (cd) имеет отри­цательное ускорение, поэтому давление впереди каждой частицы должно быть больше, чем сзади. Таким образом, зная изменение

сечения трубки тока несжимаемой жид­кости, можно качественно определить, как будет меняться давление вдоль труб­ки. График распределения давления ¹) вдоль трубки показан на рис. 284.

Дата добавления: 2015-06-28