Лекція №8. Переміщення при прямому згинанні. Розрахунки на жорскість при згинанні

Одержимо диференціальне рівняння вигнутої осі при прямому згинанні (площина дії навантажень збігається з однією з головних осей інерції). Прямолінійна вісь балки під дією зовнішніх навантажень (рис.8.1) перетворюється в плоску гладку криву і називається пружною лінією (зігнутою віссю балки).

Рис.8.1.

Прогин балки 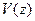- це переміщення центра ваги перерізу по нормалі до початкової осі. Максимальний прогин називається стрілою прогину і позначається f. Кут повороту 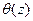перерізу - це поворот перерізу щодо початкового положення.

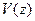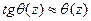Тангенс кута нахилу дотичної до вигнутої осі є перша похідна від функції : . Для малих кутів () рівняння кутів повороту можна записати у вигляді: .

Диференціальне рівняння вигнутої осі балки одержимо за допомогою рівняння Навье, у якому кривизна нейтральної осі при згинанні визначається, як: 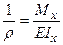. З іншого боку, з курсу аналітичної геометрії відомо, що кривизна плоскої кривої визначається як: 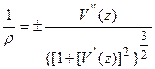. Дорівнявши праві частини цих двох залежностей, одержимо нелінійне диференціальне рівняння відносно прогину :

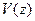. (8.1)

Для малих переміщень (у межах пружних деформацій), коли, наприклад, , квадратом першої похідної в порівнянні з одиницею можна зневажити. З обліком того, що знаки другої похідної і згинаючого моменту 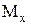збігаються, одержимо диференціальне рівняння другого порядку, що і називається диференціальним рівнянням вигнутої осі балки для малих переміщень:

. (8.1а)

Послідовно інтегруємо двічі й одержуємо рівняння для кутів повороту та прогинів:

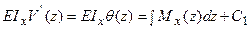, (8.2)

, (8.3)

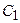де і 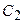- довільні постійні інтегрування, що визначаються з граничних умов.

Приклад 1. Розглянемо консольну балку, навантажену на вільному торці зосередженою силою (рис.8.2).

Рис. 8.2.

Згинальний момент у перерізі 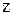: . Запишемо диференціальне рівняння пружної лінії балки: . Інтегруючи двічі це рівняння, одержимо відповідно до (8.2), (8.3):

; .

Запишемо та виконаємо граничні умови. При 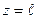кут повороту ,тобто , відкіля: 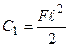. При 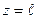прогин 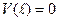,тобто: 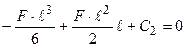, відкіля: .

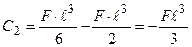З урахуванням значень 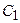і 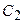рівняння пружної лінії та кутів повороту запишуться як:

; .

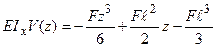Найбільші прогин та кут повороту виникають на початку координат при :

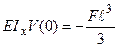, відкіля: ;

, відкіля: .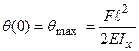

При розрахунках на жорсткість максимальні прогини балок повинні зіставлятися з прогином , що допускається. Тоді умова жорсткості при згинанні консольної балки прийме вигляд:

. (8.4)

Звідси визначається осьовий момент інерції 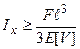, на підставі чого проектуємо переріз. Прогин, що допускається, вибирається в залежності від відповідальності конструкції з діапазону 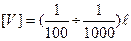, де 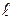- проліт балки.

Безпосереднє інтегрування диференціального рівняння пружної лінії виявляється громіздким навіть у простих випадках. Тому для визначення переміщень у балках більш прийняті енергетичні методи, що приводять до простих залежностей.

Енергетичні методи визначення переміщень.

Введемо позначення й основні поняття.

Згинальний момент від зовнішнього навантаження позначимо як 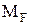. Згинальний момент від одиничної сили (моменту) - чи . Переміщення (прогин, кут повороту) від зовнішнього навантаження позначається , де перший індекс i зв'язаний з точкою чи напрямком переміщення; другий індекс j зв'язаний з причиною, що викликала переміщення. Лінійне переміщення (прогин) від одиничної сили та кутове переміщення від одиничного моменту позначаємо 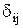, де індекс i – точка балки і напрямок переміщення; індекс j - причина, що викликала одиничне переміщення.

Інтеграл Максвелла-Мора. Розглянемо балку довжиною 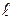, навантажену в точці 1 силою (рис.8.3). Визначимо переміщення 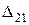(у точці 2 від сили, прикладеної в точці 1).

1. Перший стан. У точці 1 прикладемо зосереджену силу F. Прогин у точці 1 дорівнює 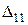, у точці 2 - 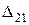. У перерізах балки виникає згинальний момент від зовнішнього навантаження 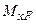. Сила F прикладається статично і виконує роботу 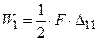на шляху 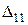(див. графік на рис.8.3.1). Визначаємо потенційну енергію деформації, виражену через згинальний момент 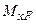, за формулою (7.12): . Але потенційна енергія деформації чисельно дорівнює роботі зовнішніх сил 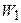, тобто: .

2. Другий стан. У точці 2 статично прикладемо одиничну силу, що, згинаючи балку, виконує роботу (див. графік на рис.8.3.2) на переміщенні . У перерізах балки виникає згинальний момент від одиничної сили. Робота одиничної сили . Потенційна енергія деформації 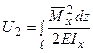. Як і в попередньому випадку .

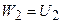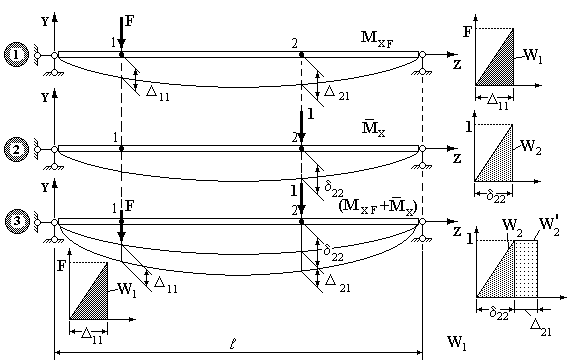
Рис.8.3.

3. Третій стан. У точці 2 статично прикладемо одиничну силу, що, деформуючи балку, виконує роботу на переміщенні (див. графік на мал.8.3.3). До деформованої балки статично у точці 1 прикладемо зосереджену силу , що, деформуючи балку з уже прикладеною одиничною силою, виконує роботу (див. графік) на переміщенні 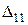. Точка 2 одержить ще переміщення 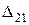, а одинична сила виконає роботу (див. графік) на переміщенні 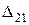. Від дії сили й одиничного навантаження в перерізах балки виникає сумарний згинальний момент . Робота двох сил визначиться як:

,

а потенційна енергія пружної деформації виразиться через сумарний згинальний момент як:

.

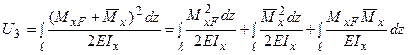Порівнюючи вирази для , після нескладних перетворень одержимо:

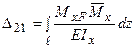. (8.5)

Дата добавления: 2015-06-28