Лекція №9.Зсув (зріз)

Деформація зсуву виникає в тому випадку, коли на площадках виділеного елемента діють дотичні напруження. Такий напружений стан називається чистим зсувом (рис.9.1).

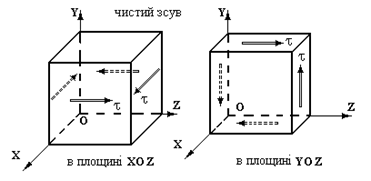
Рис.9.1.

Деформація зсуву може бути отримана (приблизно), коли на стержень діють дві рівні по величині і протилежно спрямовані сили, перпендикулярні до осі стержня. Прикладом такої дії сил на брус може бути різання ножицями металевих прутків (рис.9.2а).

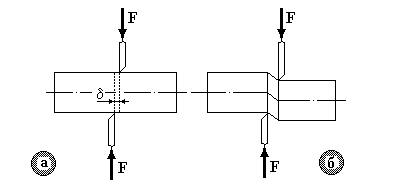
Рис.9.2.

Через те, що між діючими силами існує деяка відстань, то, звичайно, деформація зсуву супроводжується іншими видами деформацій, найчастіше деформацією згинання (рис.9.2б). Розглянемо короткий прямокутний елемент, затиснений одним кінцем, під дією сили 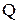(рис.9.3).

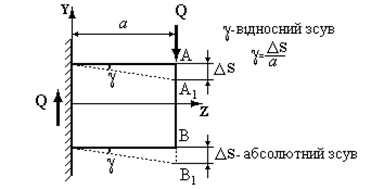
Рис.9.3.

Дія сили 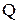викликає зсув елемента. Так як відстань між площинами, що зсуваються, мала, то виникаючим згинальним моментом зневажаємо. З рис.9.3 неважко переконатися, що 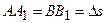. Величина 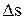називається абсолютним зсувом.

При деформації прямокутного елемента прямі кути змінюються на величину 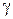, тангенс якого 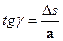. Через малість кута 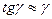, тоді 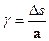– називають відносним зсувом (кут зсуву, зрушення), що являє собою відношення абсолютного зсуву 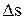до відстані 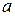між площинами.

Одержимо формулу для розрахунку напружень при зсуві. Використовуючи метод перерізів (рис.9.4а), визначимо напруження, що виникають при зсуві.

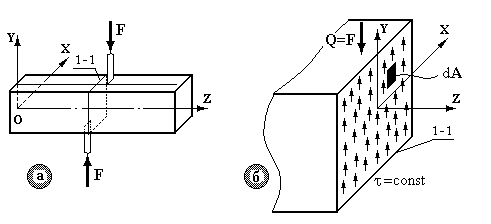
Рис.9.4.

Візьмемо переріз I-I і розглянемо рівновагу відсіченої частини (рис.9.4б), для чого складемо рівняння 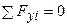: 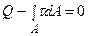. Це рівняння не може бути вирішене без геометричного аналізу деформування (невідомі величина та закон зміни 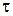). При розрахунках на зсув умовно приймається рівномірний закон розподілу 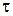по перерізу, тобто 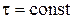. Тоді:

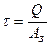, (9.1)

тут 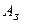– площа зрізу. Як і при будь-якому розрахунку опору матеріалів напруження в матеріалі повинні зіставлятися з напруженням, що допускається (допустиме напруження), тобто умова міцності на зріз має вигляд:

. (9.2)

Допустиме напруження приймається рівним: .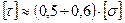

Досвідчене вивчення зсуву в матеріалах проводиться на спеціальних тонкостінних трубках, що навантажуються крутильним моментом до руйнування. У результаті цього одержують діаграму зсуву, що для пластичного матеріалу має вид (рис.9.5). По діаграмі можна визначити характеристики міцності матеріалу при зсуві (зрізі). Межа (границя) пропорційності t_пц матеріалу при зсуві – це найбільше напруження, до якого виконується закон Гука (точка 1). Межа (границя) текучості t_т – це найменше напруження, при якому відносний зсув зростає при практично постійному навантаженні (точка 2). Межа (границя) міцності t_в при зсуві – це максимальне напруження в матеріалі, при якому не настає руйнування (точка3).

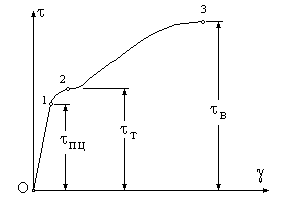
Рис.9.5.

Закон Гука при зсуві. При центральному розтяганні-стисканні між нормальним напруженням 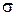, відносною деформацією 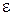та модулем подовжньої пружності Е існує залежність 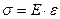, що називається законом Гука при розтяганні-стисканні. Аналогічна залежність, як показують експерименти, також існує між дотичним напруженням 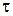, відносним зсувом 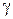та модулем зсуву 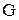, тобто закон Гука при зсуві: 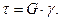(9.3)

Зв'язок трьох пружних постійних для ізотропного матеріалу (модуля подовжньої пружності 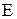, модуля зсуву 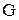і коефіцієнта Пуассона m) визначається залежністю: 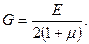(9.4)

Таким чином, модуль подовжньої пружності 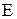, модуль зсуву 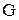і коефіцієнт Пуассона 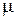характеризують пружні властивості матеріалу.

Дата добавления: 2015-06-28