Потенційна енергія деформації при крученні

Кручення стержня спостерігається в тому випадку, коли він навантажений моментами, площина дії яких перпендикулярна його осі. У цьому випадку в перерізі стержня виникає єдиний силовий фактор, що називається крутильним моментом Мк.

Розповсюдженим стержневим елементом конструкцій машин, що працюють на кручення, є вал. Відзначимо, що найбільш частіше зовнішній крутильний момент виникає у валах, що обертаються з кутовою швидкістю n (об/хв) та передають потужність K(квт) (розподільні, передавальні вали зубчатих, пасових передач). У цьому випадку на валу в місцях посадки зубчатих коліс, шківів виникає зосереджений крутильний момент:

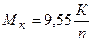[кНм]. (10.1)

Побудова епюр крутильних моментів ґрунтується на наступному: крутильний момент Мк(z) у даному перерізі чисельно дорівнює алгебраїчній сумі моментів щодо осі стержня усіх сил, розташованих по одну сторону від перерізу. Правило знаків: крутильний момент вважається позитивним, якщо обертає розглянуту область (відсічену частину) проти годинникової стрілки і навпаки. Сформулюємо правила для побудови і перевірки правильності епюр крутильних моментів.

1. При побудові епюр варто перевіряти рівновагу вала, тобто SМ_zi = 0.

2. На ділянці з інтенсивністю розподіленого моменту m = const епюра M_к лінійна, а якщо m = 0, то епюра М_к по довжині вала є кусочно-постійною по ділянках вала, тобто M_кi = const.

3. У точці прикладення зосередженого моменту на епюрі M_к спостерігається стрибок на величину зовнішнього моменту.

Експериментально встановлено, що при дії на вал двох протилежно спрямованих крутильних моментів Мк, прикладених по його кінцях (рис.10.1), вал буде закручуватися, тобто одні перерізи вала будуть повертатися щодо інших навколо осі, у той час як довжина вала залишається незмінною.

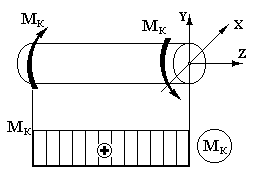
Рис.10.1. Рис.10.2.

Якщо закручувати вал аж до руйнування і представити графічно залежність крутильного моменту від кута закручування то одержимо діаграму кручення, що у випадку пластичного матеріалу має вид діаграми, показаної на рис.10.2.

На цій діаграмі також, як і на діаграмі розтягання, можна відзначити ряд характерних точок, що відповідають характеристикам матеріалу при крученні: точка 1 відповідає максимальному значенню моменту M_пц, до якого зберігається лінійна залежність між навантаженням M_к і кутом закручування j; у точці 2 спостерігається явище текучості матеріалу при крученні, коли при практично постійному моменті M_т збільшується кут закручування; точка 3 відповідає максимальному значенню моменту M_max, при якому відбувається руйнування зразка.

Дотичні напруження при крученні для стержня круглого чи кільцевого перерізу.

Попередньо розглянемо експериментальні результати кручення стержнів круглого перерізу. На валу (рис.10.3а) відзначимо утворюючі (меридіани) та поперечні перерізи (паралелі).

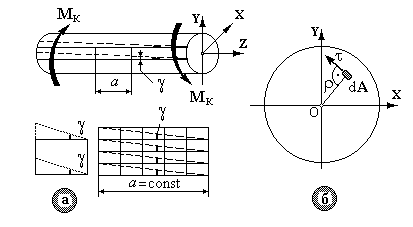
Рис.10.3.

1.При крученні поперечні перерізи стержня повертаються навколо його осі і відносно один одного.

2.Утворюючі повертаються на один і той же кут g. Квадрати перетворюються в ромби, прямі кути змінюються, як і у випадку чистого зсуву (рис.10.3а). Це свідчить про те, що виділений елементарний обсяг будь-якого шару вала знаходиться в умовах чистого зсуву.

3. Поперечні лінії після деформації не скривлюються, тобто при крученні стержня круглого перерізу дотримується гіпотеза плоских перерізів: переріз плоский і нормальний до осі до деформації залишається плоским і нормальним до осі в процесі деформації.

4.Відстані між перерізами в процесі деформації не змінюються (a = const), це підтверджує відсутність у перерізі нормальних напружень.

5.Довжина і прямолінійність радіусів перерізів не порушується, тобто дотичні напруження t у будь-якій точці перерізу перпендикулярні радіусу r (рис.10.3б).

Розглянемо стержень діаметром d, довжиною 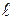, що навантажений моментом М (рис.10.4а). На відстані z виділимо елемент довжиною dz і розглянемо його рівновагу (рис.10.4б). У лівому перерізі прикладемо діючий у ньому крутильний момент Мк, а в правому перерізі замінимо Мк напруженням, що діє на елементарній площадці dA з координатами x,y, як показано на рис. 10.4б.

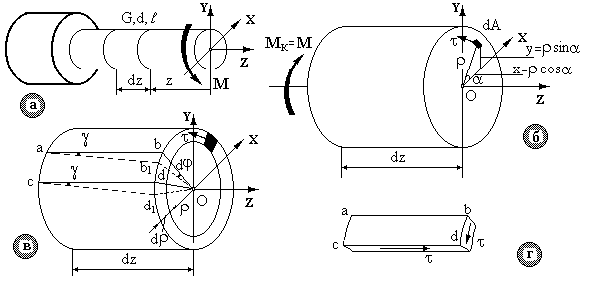
Рис.10.4.

Вважаючи, що початок координат співпадає з центром ваги О перерізу, запишемо рівняння статичної рівноваги від елементарної сили dF = tdА, що діє на площадці dA ( результуюча сила ):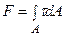

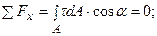(10.1)

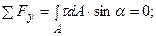(10.2)

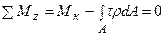. (10.3)

Так як невідома величина і закон розподілу дотичного напруження t, кут кручення, положення нуля напружень, то рівняння рівноваги вирішити неможливо. Таким чином задача є статично невизначеною. Для розкриття статичної невизначеності проведемо геометричний аналіз деформацій при крученні. Для цього з нескінченно малої ділянки вала довжиною dz виділимо нескінченно тонке кільце товщиною dr (рис.10.4в). Умовно вважаємо, що лівий переріз нерухомий. Правий переріз нескінченно малого циліндра повернеться навколо осі Z на кут dj, причому j є абсолютним переміщенням при крученні і називається кутом закручування. Утворюючі аb і сd на бічній поверхні циліндра переміщаються в положення аb₁ і сd₁ відповідно, зміщаючись на кут зсуву g.

Обчислимо довжину дуги (рис.10.4в), розглядаючи спочатку криволінійний трикутник аbb₁: 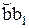= dz×tgg» dz×g, так як у межах малих пружних деформацій tgg . Розглядаючи потім криволінійний трикутник Оbb₁, величина дуги 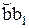виявляється рівною 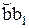=(r+dr)×dj. Зневажаючи нескінченно малими величинами другого порядку, одержуємо j, відкіля . Вводячи відносний кут закручування

, (10.4)

одержимо рівняння спільності деформацій при крученні:

(10.5)

Так як в нескінченно малому елементі аbdс виникає напружений стан чистий зсув (рис.10.4г), то в межах малих деформацій виконується закон Гука при зсуві:

(10.6) Підставляючи вираз (10.5) у (10.6), одержимо:

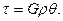(10.7) Ця залежність виражає закон Гука при крученні, на підставі якого можна зробити висновок про те, що дотичні напруження в перерізі змінюються по лінійному закону, тобто пропорційно радіусу r.

Підставляючи залежність (10.7) у рівняння (10.1) і з обліком того, що G і q є постійними величинами, а , одержимо:

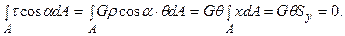
Після аналогічної підстановки залежності (10.7) у рівняння (10.2) одержимо:

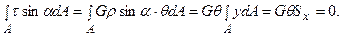
З останніх рівнянь випливає, що статичні моменти S_x, S_y площі перерізу щодо осей x,y дорівнюють нулю, оскільки G і q не дорівнюють нулю. Статичні моменти площі тільки відносно центральних осей дорівнюють нулю. Таким чином осі x,y є центральними осями перерізу. Іншими словами, центр кручення («нуль» напружень) збігається з центром ваги перерізу. Підставляючи залежність (10.7) у рівняння (10.3), і з обліком того, що інтеграл - полярний момент інерції перерізу, одержимо наступне: 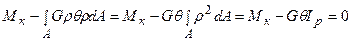, відкіля відносний кут закручування:

(10.8)

Величина GI_p називається жорсткістю стержня при крученні. З виразу (10.7) одержуємо відносний кут закручування Дорівнюючи праві частини останніх виразів, одержуємо формулу для визначення дотичних напружень при крученні стержня круглого чи кільцевого перерізів:

(10.9)

З рівняння (10.4) з урахуванням виразу (10.8) одержуємо, що кут закручування дорівнює j 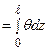Отримане рівняння являється законом Гука при кру ченні для абсолютного кута закручування. Після інтегрування по довжині стержня 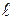одержимо, що в нашому випадку абсолютний кут закручування j стержня можна обчислити за формулою:

j 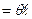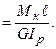(10.10)

Розподіл дотичних напружень для стержня круглого і кільцевого перерізів.Розрахунок на міцність.

З рівняння (10.9) випливає, що дотичні напруження по радіусу перерізу розподіляються лінійно (рис.10.5).

Рис.10.5.

Як видно з приведених на рис.10.5 епюр дотичних напружень, максимальні дотичні напруження виникають у крайніх точках перерізу, де r = r_max:

(10.11)

З огляду на те, що величина є полярним моментом опору перерізу, умова міцності при крученні запишеться у вигляді:

(10.12)

де [t] – допустиме дотичне напруження, обумовлене відношенням границі текучості матеріалу до коефіцієнту запасу міцності n_т, тобто: .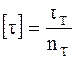

З умови міцності полярний момент опору повинний бути обраний за формулою: 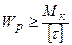. Значення полярних моментів опору для вала круглого перерізу: ; для кільцевого перерізу: 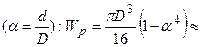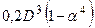. Діаметр перерізу для круглого вала обчислюється за формулою: для кільцевого вала:

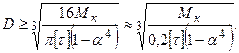
Розрахунок на жорсткість. Крім розрахунку на міцність вали розраховуються на жорсткість: 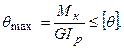(10.13)

У деяких випадках умова жорсткості при крученні складається в абсолютних кутах закручування j ([j] в радіанах – допустимий абсолютний кут закручування):

φ 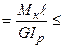max [φ]. (10.14)

З формули (10.13) полярний момент інерції I_p, що забезпечує жорсткість, визначається як: 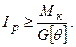Полярний момент інерції для круглого перерізу , для кільцевого 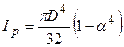≈0,1D⁴(1-α⁴). З умови жорсткості діаметр круглого перерізу: зовнішній діаметр кільцевого перерізу: .

Потенційна енергія деформації U, накопичена в пружному тілі, чисельно дорівнює роботі W зовнішніх сил, виконаної в процесі деформування пружного тіла. Розглянемо стержень довжиною ℓ навантажений крутильним моментом М (рис.10.6а).

Виріжемо елементарний відрізок dz і розглянемо його деформацію. Умовно закріпимо лівий переріз нескінченно малого елемента вала dz. При статичному навантаженні моментомM_к правий переріз елемента повернеться на кут dj (рис.10.6б). Елементарна робота dW моменту M_к на куті закручування dj при навантаженні визначається площею трикутника (рис.10.6в), тобто . Кут закручування dj визначається за формулою (10.10) і складе: 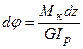. Підставивши значення dj у вираз для роботи dW, одержимо , де I_p – полярний момент інерції при крученні. Але робота dW чисельно дорівнює потенційної енергії деформації dU, тобто . Повна потенційна енергія деформації визначається як інтеграл по довжині стержня:

(10.15)

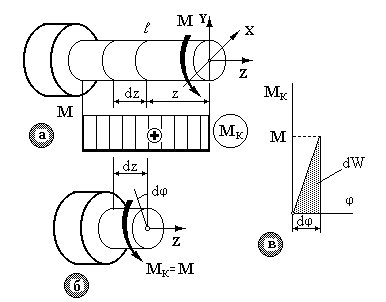
Рис.10.6.

Якщо стержень складається з декількох ділянок, потенційна енергія деформації обчислюється як сума інтегралів по ділянках:

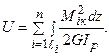(10.16)

Дата добавления: 2015-06-28